Билет n 8

Если даны a и b; b≠0 (не нулевой), то для того, чтобы a был параллелен b, необходимо и достаточно, чтобы существовало λ: a= λb.

Ясно, что введенные операции сложения векторов и (*) на число, делают множество векторов линейным пространством, в чем легко убедится, проверив выполнение известных аксиом.

Рассмотрим множество векторов, лежащих в одной плоскости и покажем, что это множество представляет линейное пространство размерностью 2.

Покажем, что существует 2-а линейно независимых вектора, лежащих в данной плоскости. Действительно рассмотрим a не параллельный b и предположим, что они линейно зависимы, т.е. λ₁a+ λ₂b=0 имеет место и хотя бы одно из λ ≠0

Пусть λ₁a += -λ₂b

а= -( λ₂/ λ₁)b, что означает коллинеарность, что противоречит условию

Покажем, что любые 3 вектора, лежащих в данной плоскости- линейно зависимы.

Рассмотрим 3 любых вектора a, b, c. Ни одна из пар не коллинеарная

Построим параллелограмм OACB: диагональ OC совпадают с с.

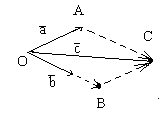
Ясно, что OC=c=OA+OB, т.к. OA паралелен a и OB паралелен b, то существуют числа λ₁,λ₂ : OA= λ₁a, OB= λ₂b₁, значит с=λ₁a+ λ₂b отсюда следует, что a, b и c линейно зависимы

Это означает, что множество векторов, лежащих в этой плоскости образуют линейное пространство с размерностью 2. В качестве базиса можно брать любых 2 непараллельных вектора.

a, b, c - компланарны, если они лежат в одной или в параллельных плоскостях. Легко показать, что любые3 из комланарных – линейно независимы, а любые 4 – линейно зависимы. Следовательно множество всех векторов представляют линейное пространство размерности 3 и в качестве базиса можно брать любые 3 некомпланарных вектора.

Рассмотрим в пространстве прямоугольную систему координат и введем единичные вектора i, j, k, которые направлены по x, y, z соответственно │j│=│i│=│k│=1

Ясно, что i, j, k не компланарны => будут базисом. Тогда любой a=α₁i+α₂j+ α₃k Причем α₁, α₂, α₃ – координаты a в базисе i, j, k: a={ α₁, α₂, α₃ }

Легко показать, что α₁, α₂, α₃ –проекции a на x, y, z :

│a│=( α₁² +α₂² +α₃² )^1/2, j, i, k

cos α= α₁/│a│- направляющие косинусы

cos β= α₂/│a│

cos φ = α₃/│a│

φ, α, β- углы составляемые a c осями x, y и z

Легко видеть, что Σсa² =1 (cos²α + cos²β + cos²φ =1 )

Билет N 9

Пусть даны a,b

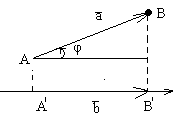AB=a

A’B’-компонента a по b

Проекция a на b: (Пр_ba) = │a│cos φ

Билет N 10

Скалярное произведение.

Скалярное произведение a на b называется число, равное произведению длин этих векторов на косинус угла между ними.

a*b=(a,b)= │a││b│cosφ, φ-угол между a и b.

Св-ва :

1 a*b=b*a

2 α a*b=a* αb= α (a*b)

3 (a+b)c=a*c + b*c

a*b=│a││b│cosφ = Пр_ba*│b│

(a +b)*c= Пр_с(a +b)* │c│=( Пр_сa+ Пр_сb)*│c│= Пр_сa*│c│+Пр_сb*│c│=a*c +b*c

4 Пусть даны a и b. Они ортогональны, если они перпендикулярны. Чтобы a и b были ортогональны необходимо и достаточно, чтобы их произведение=0.

a*b =│a││b│cosφ=0

5 Выражение через координаты

Если a и b заданы своими координатами в ортонормированном базисе, то скалярное произведение этих векторов= сумме произведений одноименных координат.

Пусть a= a_xi +a_yj+ a_zk

b= b_xi +b_yj+ b_zk

a*b= (a_xi +a_yj+ a_zk) (b_xi +b_yj+ b_zk)= a_xb_x(i*i)+ a_xb_y(i*j)+ a_xb_z(i*k)+ a_yb_x(j*i)+ a_yb_y(j*j)+ a_yb_z(j*k)+a_zb_x(k*i)+ a_zb_y(k*j)+ a_zb_z(k*k)= a_xb_x+ a_yb_y+ a_zb_z

cos φ = (a_xb_x+ a_yb_y+ a_zb_z )/ [( a_x² +a_y² +a_z² ) ( b_x² +b_y² +b_z² )] ^1/2

Билет N 11

Векторное произведение.

Пусть даны a и b . Векторным произведением a и b называется: ab=[a; b]

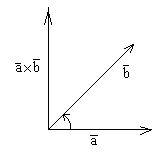
1 длина которого= │ab│=│a││b│sin φ

2 (ab) ┴ a, b

3 если смотреть с конца (ab) на плоскость перемножаемых a и b, то поворот a к b на наименьший угол происходит против часовой стрелки :

Свойства :

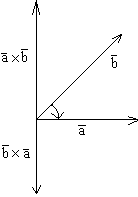
1 ab= - ba

2 [α a, b]=[a, α b]= α[a, b]

3 (a+ b)c=ac+ bc

4 Модуль векторного произведения a и b численно равен площади параллелограмма, построенного на перемножаемых векторах

│ab│=Sпарал.

5 Выражение векторного произведения через координаты выражения

a= a_xi +a_yj+ a_zk

b= b_xi +b_yj+ b_zk

ab= (a_xi +a_yj+ a_zk)(b_xi +b_yj+ b_zk)= a_xb_x(ii)+ a_xb_y(ij)+ a_xb_z(ik)+ a_yb_x(ji)+ a_yb_y(jj)+ a_yb_z(jk)+a_zb_x(ki)+ a_zb_y(kj)+ a_zb_z(kk)= a_xb_yk - a_xb_zj – a_yb_xk+ a_yb_zi+ a_zb_xj – a_zb_yi = (a_yb_z – a_zb_y)i + (a_zb_x – a_xb_z)j +(a_xb_y – a_yb_x)k

Легко показать, что ab= i j k

a_x a_y a_z

b_x b_y b_z

Билет N 12

Cмешанное произведение трех векторов.

Пусть даны a,b,c. Смешанным произведением a, b и c называется число a(bc)

Свойства :

1 Модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах :

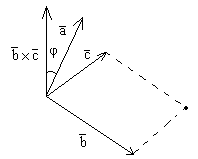
│a (bс)│=│a││bc│cos φ

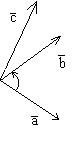
Пусть даны 3 вектора a, b и c. Говорят, что a, b и с образуют правую тройку, если, смотря с конца вектора с на плоскость aиb, поворот от а к b на наименьший угол, осуществляется против часовой стрелки. В обратном случае – это левая тройка.

2 Если рассмотреть тройку векторов a, b, c, то легко видеть, что при круговой замене:

наименование тройки не меняется

a (bс)= b (ca)= c (ab)=(a, b, c)

3 Выражение смешанного произведения через координаты :

a= a_xi +a_yj+ a_zk a_x a_y a_z

b= b_xi +b_yj+ b_zk (a, b, c)= b_x b_y b_z

с= с_xi +с_yj+ с_zk, то c_x c_y c_z

Из того св-ва, что │(a, b, с)│- есть V параллелепипеда сразу следует то, что, для того чтобы три вектора a, b, c были компланарны, необходимо и достаточно, что бы их смешанное произведение= 0