Аналитическая геометрия

7

§14. Прямая в R3. 1

§15. Плоскость в R3. 3

§16. Задачи на прямую и плоскость в R3. 4

ТР по теме "Аналитическая геометрия". 6

§14. Прямая в R³.

Аксиома геометрии: «через точку проходит единственная прямая L, параллельная другой прямой».

На «векторном языке»: через заданную точку М_о(x_o,y_o,z_o) можно провести единственную прямую L, параллельную заданному вектору S_L=[s_x;s_y;s_z]^t

LR³:L S_L  M₀L

Назовем этот вектор S_L=[s_x;s_y;s_z]^t «направляющим вектором» прямой L и выведем уравнение прямой, которое связывает координаты любой точки прямой M(x,y,z)L.

.

Например,

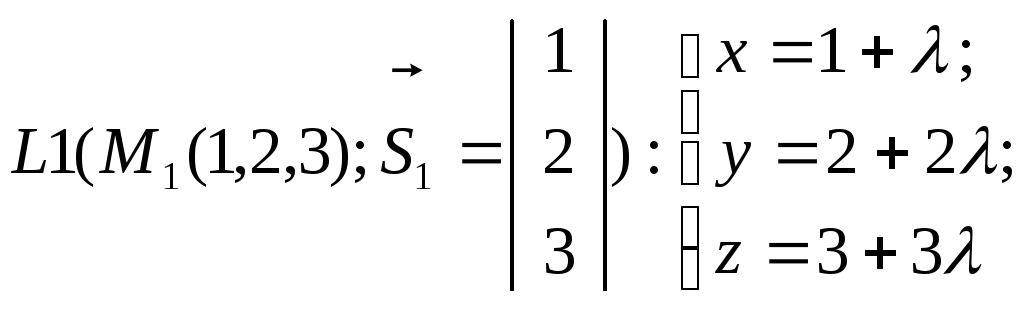
Замечания.

1) Уравнения (1),(2) называются "параметрическими" потому, что каждая точка прямой определяется значением параметра -

2) L1||L2 <=>S₁||S₂<=> S₁=λS₂. -условие параллельности прямых.

L1L2 <=> S₁S₂<=> (S_1,S₂)=0 -условие перпендикулярности прямых.

3)Угол между прямыми  угол между их направляющими векторами

!!!»Заповедь»:»Решение задач аналитической геометрии следует начинать с определения параметров прямой L(M₀;S_L).

-----------------------------------------------------------------

Примеры.

[1]. Прямая через две заданные точки :

[2]. Точка пересечения двух прямых

определяется, очевидно, значениями двух параметров λ_P(L1), μ_P(L2), которые должны удовлетворять системе 3 уравнений:

Так как 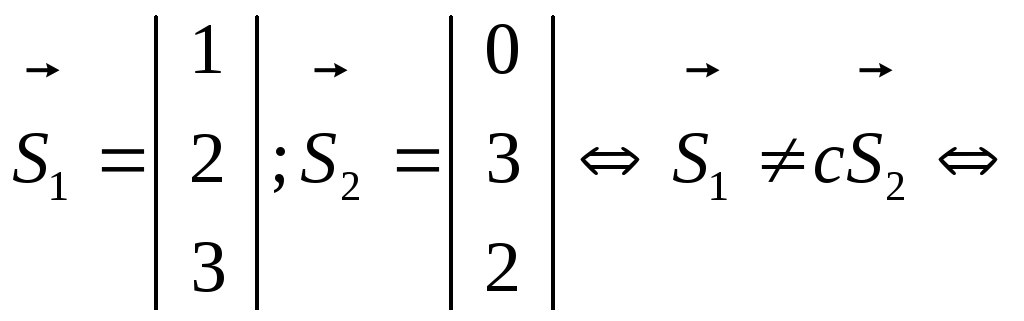L1,L2 не параллельны L1,L2- скрещивающиеся прямые.

§15. Плоскость в R³.

Из аксиом геометрии следует, что через любую заданную точку М_о(x_o,y_o,z_o) проходит единственная плоскость α, перпендикулярная заданному вектору n_α=[n_x;n_y;n_z]^t, называемому нормальным вектором плоскости.

Выведем уравнение плоскости α(M₀(x₀,y_0,z₀); n_α).

M₀M=r-r₀ n_α <=> (r-r₀ ,n_α)=0<=>

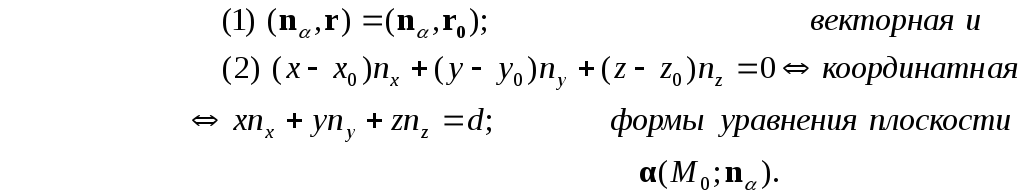
Следствия.

(1). Всякое линейное относительно координат уравнение задает в R³ плоскость, при этом (а)коэффициенты при координатах, находящихся в одной части уравнения, являются координатами направляющего вектора плоскости, а три координаты точки плоскости определяются одним уравнением.

Например,

• уравнение x=y в R³ определяет плоскость α(M₀(1,1,0);n_α=[1,-1,0]^tOZ)OZ;

• z=2 n_=[0;0;1]^tOZ  α||XOY;

(2) Условие параллельности плоскостей : α||β <=> n_α||n_β <=> n_α=λn_β.

(3) Условие перпендикулярности плоскостей : αβ <=> n_αn_β <=> (n_α,n_β)=0.

(4) Угол между плоскостями равен углу между нормальными векторами этих плоскостей (,)=(n_α,n_β) (cos(α,β)=cos(n_α,n_β)=( n_α,n_β)/||n_α||/||n_β||.

(5) Угол между прямой L и плоскостью α и угол между соответствующими векторами S_L,n_α связаны соотношением (L,α)+(S_L,n_α)=π/2, поэтому sin(L,α)= sin[π/2-(n_α,n_β)]=cos(S_L,n_α)=.

=====================================================================

Примеры. α(A(1,1,0);n_α=[1,2,3]^t); (B(1,1,0);n_=[1,1,1]^t);

L(F(1;1;1); S_L=[3,2,1]^t; C(1;0;1)

1)(,)=( n_α,n_)=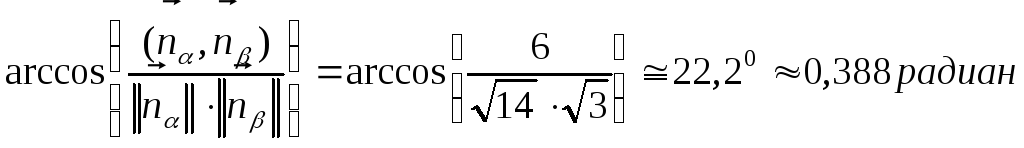

2)(L, )= π/2-(S_L,n_α)(L, )=arccos(S_L,n_α)=arcos(10/14)0.775рад44.4⁰

3)C(плоскость через заданную точку параллельно заданной плоскости)

 (C;n_=n_): 1(x-1)+2(y-0)+3(z-1)=0x+2y+3z=4

4)CL (плоскость через заданную точку перпендикулярно заданной прямой)

 (C;n_=S_L): 3(x-1)+2y+1(z-1) 3x+2y+z=4

§16. Задачи на прямую и плоскость в R³.

Пусть заданы своими координатами точки

A(1;1;2); B(1;2;1);C(2;1;1);D(1;2;3)

[1] Плоскость через три заданные точки, не лежащие на одной прямой.

A,B,C  ABn_AC  n_= AB x AC=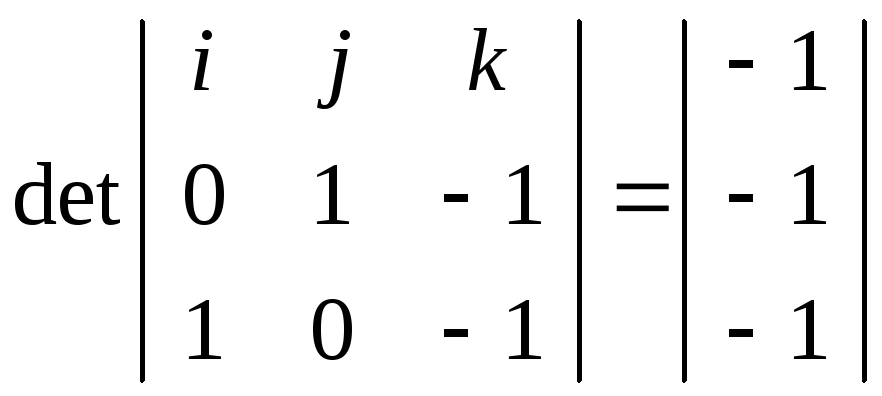

(A; n_=[1;1;1]^t): 1(X-1)+1(Y-1)+1(Z-2)=0 x+y+Z=4

[2] Прямая как линия пересечения плоскостей L=(B;n_=[1;-1;1]^t).

L(M_L-?;S_L-?)

M_L,:

S_L: n_S_Ln_ S_L= n_xn_=

[

n_=[1;1;1]^t

3]. Расстояние от заданной точки D(1,2,3) до заданной плоскости α.

Выберем любую точку плоскости A и вычислим вектор

АD=[0;1;1]^t.

Очевидно, что модуль его проекции на вектор нормали плоскости равен искомому расстоянию

[4]. Проекция точки D на плоскость α.

а) Проведем через точку D прямую L, перпендикулярную плоскости.

б) Найдем точку пересечения прямой L и плоскости α:

[5]. Точка D1, симметричная заданной точке d относительно заданной плоскости α.

а) Найдем точку

б) Запишем равенство для направленных отрезков:

r_D1=r_A+2AP=r_A+2(r_P -r_A)=2r_P-r_A=[-1;1;2]^t 

[6]. Расстояние от заданной точки A(1,1,2) до заданной прямой L(M_L(0,2,2); S_L=[2,0,-2]^t).

а) Проведем через точку А плоскость, перпендикулярную прямой L.

б) Найдем точку P пересечения плоскости α и прямой L ₃ : 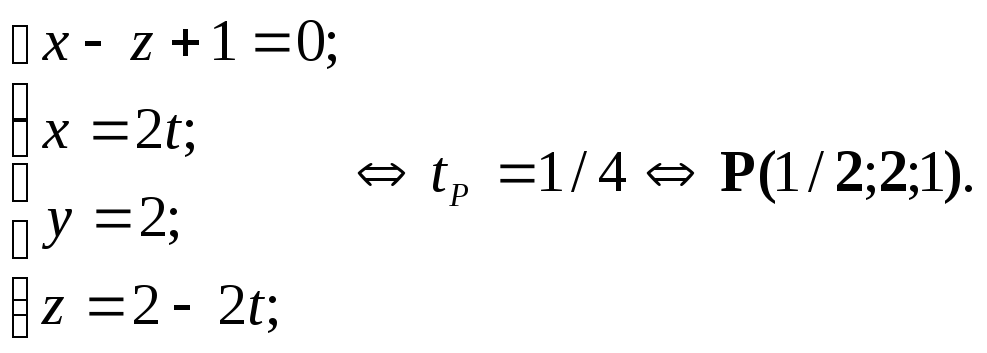в)Найдем норму |AP|=||[-1/2;1;-1]^t||=1.5

===========================================================================

ТР по теме "Аналитическая геометрия".

Задание. По заданным своими координатами точкам A1,A2,A3,A4

ВАР.	A1	A2	A3	A$
	x1,y1,z1	x2,y2,z2	x3,y3,z3	x4,y4,z4

1. Записать уравнения плоскостей a(A1,A2,A3) и b(A,A3,A4) .

2. Найти косинус угла и угол в радианной мере между этими плоскостями.

3. Записать уравнение прямой L(A1,A4).

4. Найти синус угла и угол между прямой L и плоскостью a.

5. Найти расстояние от точки A4 до плоскости a.

6. Найти точку A5, симметричную точке A4 относительно плоскости a.

================================================================