20

Глава II. Элементы линейной алгебры и аналитической геометрии. 1

§1. Матрицы: определения; линейные операции. 1

§3. Системы линейных алгебраических уравнений (СЛАУ): решение; равносильные преобразования системы; матричная форма записи. 3

§4. Метод Жордана-Гаусса (метод полного исключения) решения СЛАУ. 5

ТР-1.6 «Решение матричных уравнений». 9

§5. Матричные уравнения. Обратная матрица. 12

§6 Определитель матрицы. 13

§7. Свойства и вычисление определителей. 15

§8. Теорема и формулы Крамера. 17

20

Глава II. Элементы линейной алгебры и аналитической геометрии.

§1. Матрицы: определения; линейные операции.

Определения.

1.Матрицей размерности “mxn” называется прямоугольная таблица, в “m” строках и “n” столбцах которой расположены mn ее элементов: A_mxn=[a _ik] ; a _ik-элемент “i” строки и “k” столбца i=1:m; k=1:n. Элементами матрицы могут быть числа, функции, матрицы. В дальнейшем будем по умолчанию рассматривать числовые матрицы a_ikC(R).

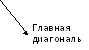
2. Квадратная матрица порядка “m” m=n:

 диагональная матрица – D_m=diag[d₁,d₂,…, d_m]- квадратная матрица, на главной диагонали которой находятся элементы d₁,d₂,…, d_m, а остальные элементы – нулевые: d_ii=d_i  d_ik=0;ik.

 единичная матрица порядка “m”: I_m=diag[1,1,…,1]

Например,

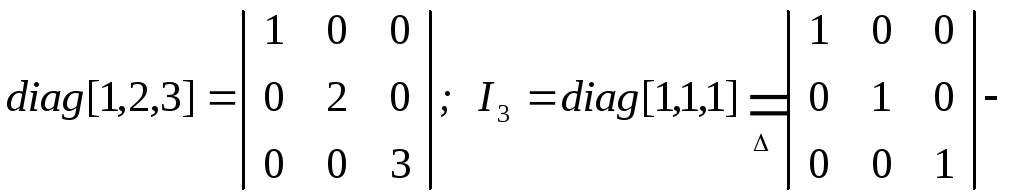единичная матрица 3-го порядка.

3.Транспонированная матрица A^t: - при транспонировании матрицы «переставляются» ее строки и столбцы и изменяется размерность. 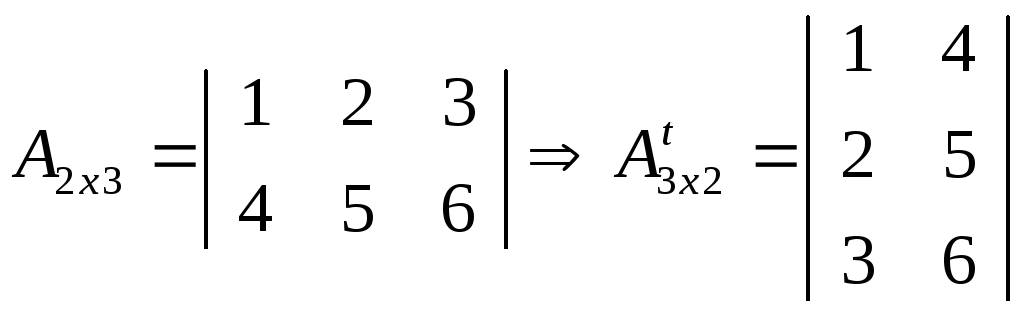. Очевидно, что(A^t)^t=A.

4. Для матриц одинаковой размерности введем «поэлементные» операции:

• равенство: A=B b_ik= a_ik;

• умножение на скаляр (число) dC(R): B=dA b_ik= da_ik;

• сложение и вычитание: C=AB c_ik= a_ik b_ik;

Например,

§2. Умножение матриц; матричная запись системы линейных алгебраических уравнений (слау).

Определение. Произведением матриц согласованных размерностей A_mхkB_kхn называется матрица размерности mxn C_mxn, элементы которой вычисляются по правилу «строка на столбец»: элемент C_ij i-строки и j-столбца равен сумме произведений элементов “i” строки левого множителя на соответствующие элементы “j” столбца правого множителя.

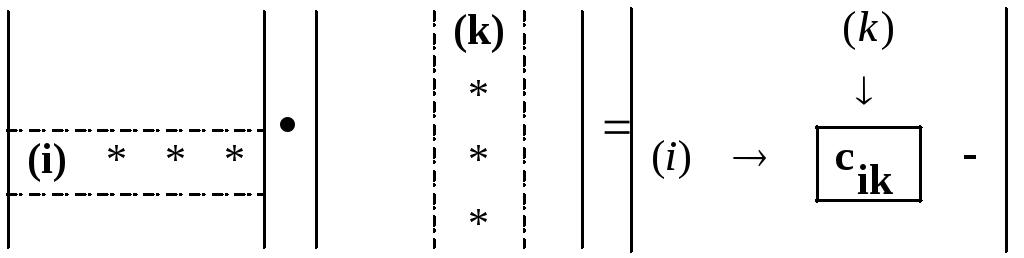
Например,

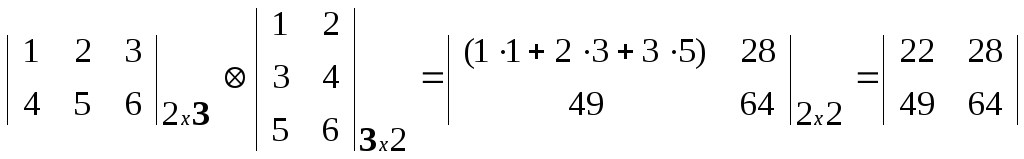НО

Следствия.

1) Произведение определено не для любых матриц, например,

2) В общем случае АВ#BA, даже если оба произведения определены

экз.?: для каких матриц AB  BA ?

3) :

4)Можно доказать (экз.+1), что если определено произведение AB, то (а) B^tA^t и (б)(AB)^t=B^tA^t- при транспонировании произведения матриц множители переставляются и заменяются на транспонированные матрицы;

Док-во. C_mxL=A_mxnB_nxLC^t_Lxm 

например,

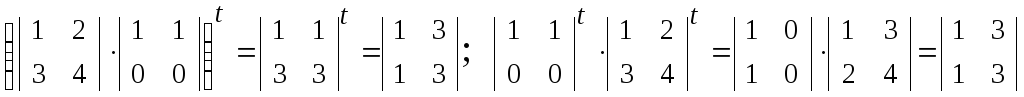
5) Пусть А_mxk и В_mx1 –заданные числовые матрицы, а X_kx1=[x1,x2,..,x_k]^t – матрица-столбец неизвестных, так что определено матричное уравнение A_mxkX_kx1=B_mx1.

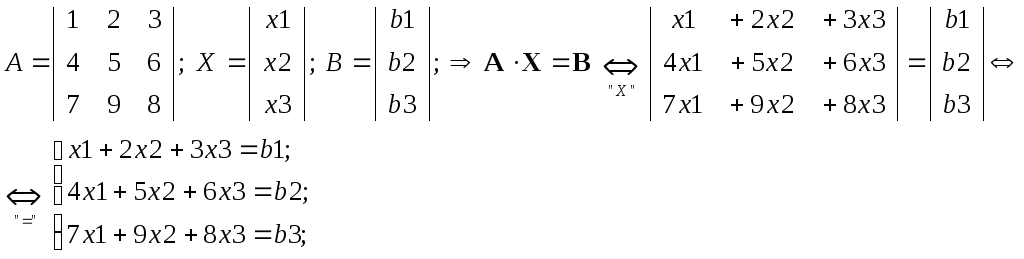
Таким образом, матричное уравнение A_mxkX_kx1 = B_mx1 равносильно системе “m” линейных алгебраических уравнений с “n” неизвестными, при этом матрица А называется матрицей системы, а матрица, составленная из матрицы системы и матрицы-столбца ее правых частей |A|B|=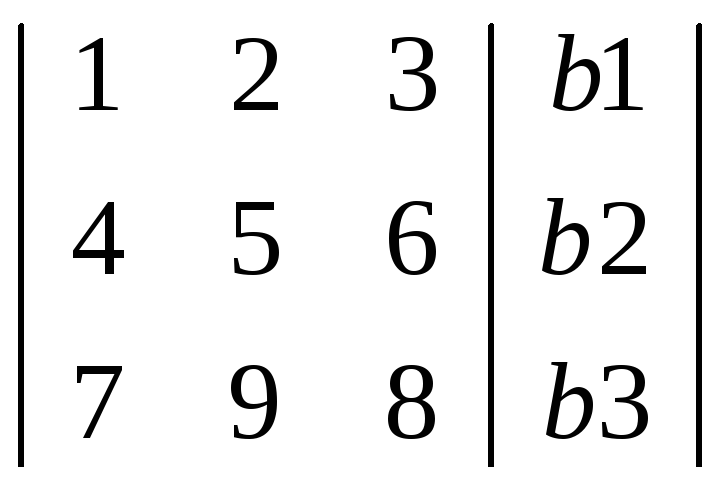- расширенной матрицей системы.

§3. Системы линейных алгебраических уравнений (слау): решение; равносильные преобразования системы; матричная форма записи.

Определения.

1. Системой “m” линейных алгебраических уравнений с “n” неизвестными x₁, x₂, .., x_n (m<,=,>n) называется система вида

;

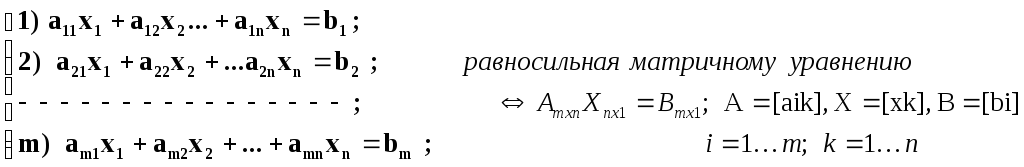(2)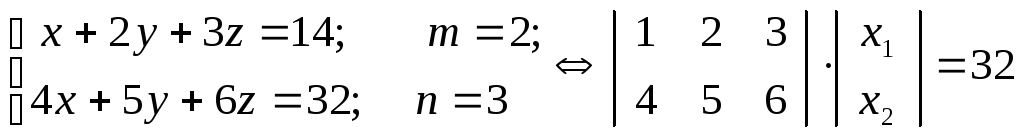(3)

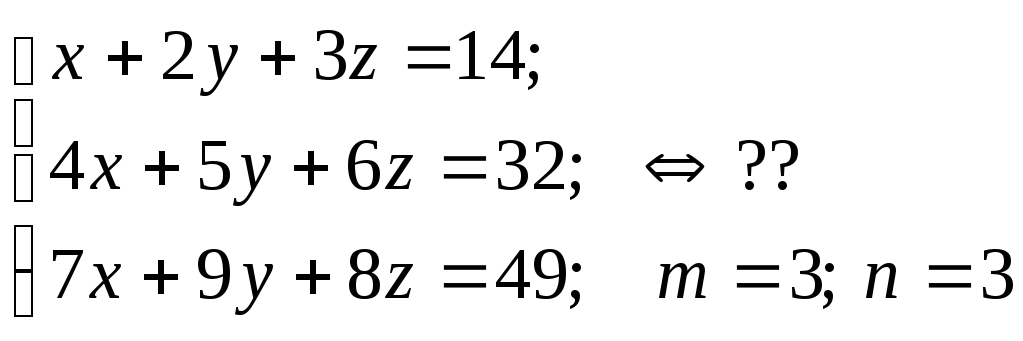
2. Решением СЛАУ называется набор “n” чисел x₁=c1, x2=c2,.., x_n=c_n (матрица-столбец X=[c1,c2,…,cn]^t₎, при подстановке которых в систему каждое уравнение превращается в верное числовое равенство.

3. Две СЛАУ называются равносильными, если равны множества их решений. Например, (2) и (3) - не равносильные СЛАУ.

Алгоритм «решения» системы:

1. Существует ли решение ? --> система называется несовместной (множество решений - пустое множество ).

2. 

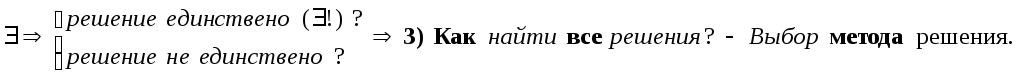
4)Выбранным методом находится множество решений(в том числе и ).

Рассмотрим простейшую систему ax=b (m=n=1).

Например, m=n=1: ax=b.

Таким образом, СЛАУ может быть несовместной, может иметь единственное решение и может иметь множество решений.

Поскольку при умножении уравнения на число и при «сложении» уравнений системы соответствующие операции выполняются над числами -коэффициентами при неизвестных и правыми частями уравнений, равносильные преобразования системы естественно выполнять над таблицей, составленной из этих чисел– над расширенной матрицей системы (РМ), составленной из матрицы (коэффициентов) системы (А_mxn) и матрицы-столбца (В_mx1) правых частей: РМ=[A|B]_mx(n+1)

Таблица равносильных преобразований.

СЛАУ	РМ	Обозначение операции
Перестановка уравнений, Перестановка слагаемых Ij	Перестановка строк, Перестановка столбцов А Ij	Pij ; 
«Умножение» “i” –го уравнения на число 0	«Умножение» строки “i” на число 0	Mi(): (i) (i)
Замена “i”-уравнения на его сумму с “j”уравнением, умноженным на число 	Замена “i”-строки на ее сумму с “j” строкой, умноженной на число 	Sij(): (i)(i)+ (j)

Например,