6.3 Теоретические вопросы к защите расчетного задания № 6
Какую случайную величину называют непрерывной?
Как задают закон распределения непрерывной случайной величины?
Что называют плотностью распределения непрерывной случайной величины?
Сформулируйте характеристические свойства плотности распределения.
Чему равна вероятность того, что непрерывная случайная величина примет одно определенное значение?
Как с помощью функции распределения найти вероятность того, что непрерывная случайная величина попадет в интервал (a, b)?
Как с помощью плотности распределения найти вероятность того, что непрерывная случайная величина попадет в интервал (a, b)?
Как определяется математическое ожидание непрерывной случайной величины?
Как выглядит формула, определяющая дисперсию непрерывной случайной величины?
Какое распределение вероятностей называется равномерным?
Какой вид имеет функция распределения случайной величины, равномерно распределенной на отрезке [а; b]?
Как вычислить вероятность попадания значений равномерно распределенной случайной величины в заданный промежуток?
Как определяется показательное распределение случайной величины?
Какой вид имеет функция распределения случайной величины, распределенной по показательному закону?
Какое распределение вероятностей называется нормальным?
Какими свойствами обладает плотность нормального распределения? Как влияют параметры нормального распределения на вид графика плотности нормального распределения?
Как вычислить вероятность попадания значений нормально распределенной случайной величины в заданный промежуток?
Как вычислить вероятность отклонения значений нормально распределенной случайной величины от ее математического ожидания?
Сформулируйте правило «трех сигм»?
Чему равны математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины, распределенной по равномерному закону на отрезке [а; b]?
Чему равны математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины, распределенной по показательному закону с параметром λ?
7 Системы случайных величин
7.1 Теоретические сведения и примеры решения задач
Функция распределения системы двух случайных величин (X, Y):
.
Распределение двумерной дискретной случайной величины (X, Y):
.
Распределения компонент двумерной дискретной случайной величины (X, Y):
,
i
= 1, 2, …
,
j
= 1, 2, …
Плотность распределения двумерной непрерывной случайной величины (X, Y):
.
Выражение для функции распределения непрерывной случайной величины (X, Y):
Характеристическое свойство плотности совместного распределения (X, Y):
.
Плотности распределения составляющих двумерной непрерывной случайной величины (X, Y):
,
.
Математические ожидания и дисперсии составляющих двумерной непрерывной случайной величины (X, Y):
,
,
,
.
Корреляционный момент двумерной дискретной случайной величины (X, Y):
.
Корреляционный момент двумерной непрерывной случайной величины (X, Y):
.
Здесь
и
−
математические ожидания составляющих
Х и
Y
соответственно.
Коэффициент корреляции двумерной случайной величины (X, Y):
,
где
и
– средние квадратические отклонения
составляющих Х
и Y
соответственно.
Условие независимости дискретных случайных величин Х и Y:
,
т.е.
.
Условие независимости непрерывных случайных величин Х и Y:
.
Задача.
Случайная величина (Х,
Y)
равномерно распределена внутри эллипса
.
Найти: а) плотность совместного
распределения (Х,
Y),
б) плотности распределения и математические
ожидания составляющих Х
и Y;
в) корреляционный момент и коэффициент
корреляции
Х и
Y;
г) вероятность
попадания (Х,
Y)
в
область G,
определяемую соотношениями
,
.
Доказать зависимость Х
и Y.
Решение.
а) В данном случае
(с
= const)
внутри эллипса, вне эллипса
.
Константу с
найдем, воспользовавшись
характеристическим
свойством двумерной плотности вероятности
,
из уравнения
,
или
,
где D – область, ограниченная данным эллипсом.
Известно, что
,
где
– площадь области D.
В данном случае
.
Подставляя это значение в последнее
уравнение, выражаем с:
.
Таким образом, плотность совместного
распределения Х
и Y
имеет вид:
.
б) Плотности распределения составляющих Х и Y найдем, взяв интегралы по переменным у и х соответственно:
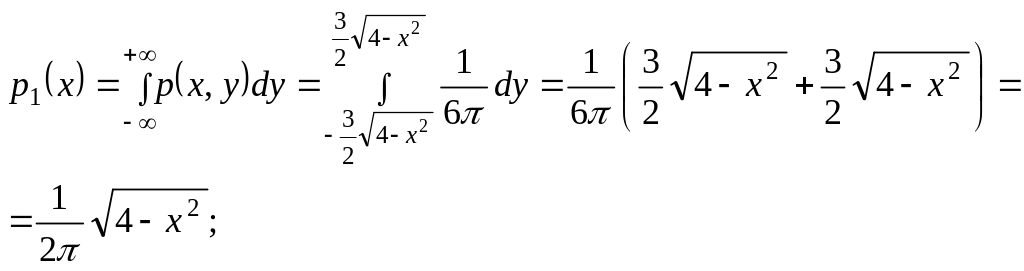
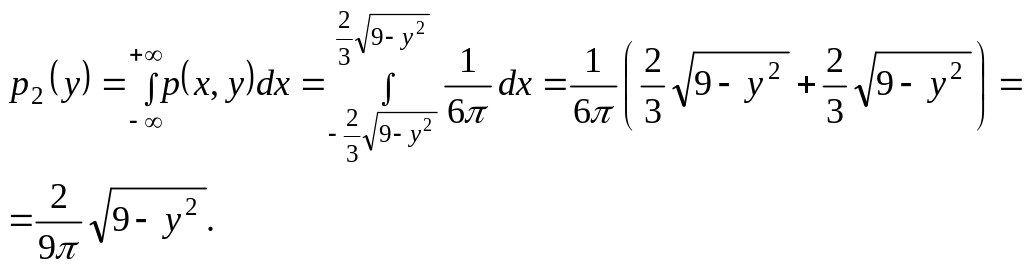
Математические ожидания составляющих Х и Y системы вычислим следующим образом:
,
.
Математические ожидания равны нулю как интегралы от нечетных функций в симметричных пределах интегрирования.
в) Найдем корреляционный момент системы двух случайных величин Х и Y, для чего воспользуемся формулой:
.
В
данном случае имеем:
.
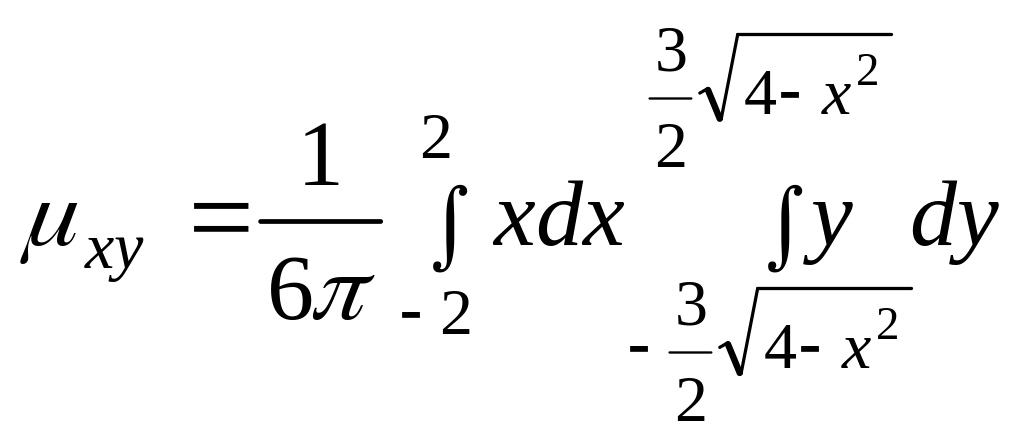Внутренний интеграл представляет собой интеграл от нечетной функции в симметричных пределах интегрирования, он равен нулю, следовательно, корреляционный момент также равен нулю.
г) Определим вероятность попадания (Х, Y) в область G, определяемую соотношениями , :
.
Случайные
величины Х
и Y
являются зависимыми, так как
не
выполняется равенство
.
В самом деле,
.