
Matematika
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ
Государственное образовательное учреждение высшего профессионального образования «Алтайский государственный технический университет имени И.И. Ползунова»
Бийский технологический институт (филиал)
О.Д. Ростова, Т.М. Тушкина
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Методические рекомендации с вариантами заданий к типовому расчету по курсу линейной алгебры и аналитической геометрии для студентов специальностей 071900 «Информационные системы и технологии», 190900 «Информационно-измерительная техника и технологии», 351400 «Прикладная информатика (в экономике)»
Бийск 2005
УДК 517
Ростова О.Д., Тушкина Т.М. Элементы линейной алгебры и аналитической геометрии: Методические рекомендации с вариантами заданий к типовому расчету по курсу линейной алгебры и аналитической геометрии для студентов специальностей 071900 «Информационные системы и технологии», 190900 «Информационно-измерительная техника и технологии», 351400 «Прикладная информатика (в экономике)».
Алт. гос. тех. ун-т, БТИ. − Бийск. Изд-во Алт. гос. тех. ун-та, 2005. − 34 с.
Данная работа предназначена для студентов первого курса факультета ИТАУ дневного отделения.
Каждый вариант типового расчета содержит 12 задач по темам: линейные преобразования, линейные отображения, прямые на плоскости и в пространстве, линии второго порядка, плоскости и поверхности второго порядка. Для защиты типового расчета студенту необходимо решить все задания своего варианта и выполнить теоретические упражнения.
Рассмотрены и одобрены на заседании кафедры ВМиМФ.
Протокол №42 от 4.02.05
Рецензент: доцент БПГУ Заворуева В.Г. (г. Бийск)
©Ростова О.Д., Тушкина Т.М., 2005
©БТИ АлтГТУ, 2005
2

ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ ПО РАЗДЕЛУ «ВЕКТОРНАЯ АЛГЕБРА»
1.Почему тождество a3 - b3 = (a - b)(a2 + ab + b2 ) не имеет смысла для векторов?
2.Стороны параллелограмма α1 равны диагоналям параллело-
грамма α2 . Как связаны их площади S1 и S2 ?
3. Векторы AC = m и BD = n служат диагоналями параллело-
грамма ABCD. Выразить векторы AB, BC, CD и DA через m и n . 4. Найти сумму ab + bc + ca , если a, b, c − три орта, причем
a + b + c = 0.
5. Зная векторы a и b , на которых построен параллелограмм, выразить через них вектор, совпадающий с высотой параллелограмма,
перпендикулярной к стороне a .
6.Найти (a ´b) 2 + (a ×b) 2 .
7.Показать, что, если a ^ b и a ^ c , то [a,[b, c]] = 0 .
8.Доказать, что a, b, c компланарны, если
a ´b + b ´ c + c ´ a = 0 .
9.Стороны ромба совпадают с векторами a и b , приведенными
кодному началу. Доказать, что диагонали ромба перпендикулярны.
10. Найти объём параллелепипеда, построенного на векторах:
p = a + b + c; q = a + b - c; r = a - b + c .
3
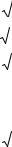
РАСЧЁТНОЕ ЗАДАНИЕ 1
Найти координаты радиус-вектора точки А в новой системе координат при повороте осей на угол α , зная координаты нового начала
O1 (x0 , y0 ) и координаты (x1 ; y1 ) радиус-вектора точки А в исход-
ной прямоугольной системе. |
|
|
|
|
|
||||
1.1 |
x0 |
= 3; |
y0 |
= 2; |
x1 = 12; |
y1 |
= 4; |
α = arctg3. |
|
1.2 |
x0 |
= 19; |
y0 |
= 4; |
x1 |
= 7; |
y1 |
= 5; |
α = arcsin0,8. |
1.3 |
x0 |
= −9; |
y0 = 1; |
x1 |
= 2; |
y1 |
= −1; α = arctg0,75. |
||
1.4 |
x0 |
= 7; |
y0 |
= −3; |
x1 |
= 4; |
y1 |
= 6; |
α = arcsin0,6. |
1.5 |
x |
|
= 11; |
y |
|
|
= 13; |
|
x |
= −2; |
y |
|
= 3; |
α = arccos |
15 |
. |
||||||||||||||||
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
17 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.6 |
x |
|
= 4; |
y |
|
|
= −2; |
|
|
x |
= 7; |
|
y |
|
= 11; |
|
α = arcsin |
8 |
. |
|||||||||||||
0 |
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
17 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.7 |
x0 |
= −3; |
|
y0 |
= 5; |
|
|
x1 |
= 6; |
y1 |
= 14; |
α = arctg 2. |
||||||||||||||||||||
1.8 |
x0 |
= 3; |
y0 |
|
= −3; |
|
|
x1 |
= 9; |
|
y1 |
|
= −1; |
|
α = arccos0,6. |
|||||||||||||||||
1.9 |
x |
|
= 6; |
y |
|
|
= 7; |
x |
= 2; |
y = 5; α = arccos |
8 |
. |
|
|
|
|
||||||||||||||||
0 |
0 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.10 |
x |
|
= 5; |
y |
|
|
= −1; |
|
x |
= 3; |
|
y |
|
= 2; |
α = arcsin |
15 |
. |
|
|
|
||||||||||||
0 |
0 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= 1; |
|
|
= 4; |
x1 = 7; |
|
= −2; |
|
α = arctg2 |
|
|
|
|
|
|||||||||||||||||
1.11 |
x0 |
y0 |
|
y1 |
|
2. |
||||||||||||||||||||||||||
|
|
= −2; |
|
|
= 8; |
|
|
= 1; |
|
|
|
= 2; |
|
α = arctg3 |
|
|
|
|
|
|
||||||||||||
1.12 |
x0 |
|
y0 |
|
x1 |
|
y1 |
|
|
7. |
|
|||||||||||||||||||||
|
|
= 2; |
|
= −9; |
|
x1 = 4; |
|
= 1; |
|
α = arctg 2 |
|
|
|
|
||||||||||||||||||
1.13 |
x0 |
y0 |
|
y1 |
|
6. |
||||||||||||||||||||||||||
1.14 |
x0 |
= 8; |
y0 |
= 15; |
|
|
x1 |
= 2; |
|
y1 |
|
= 4; |
|
α = 0,5arctg 2. |
||||||||||||||||||
1.15 |
x0 |
= 9; |
y0 |
|
= −7; |
|
|
x1 |
= 5; |
|
y1 |
|
= 2; |
α = 0,5arccos0,36. |
||||||||||||||||||
|
|
= 13; |
|
|
= 7; |
|
|
|
= 2; |
|
|
= 9; |
|
α = arctg 4 |
|
|
|
|
||||||||||||||
1.16 |
x0 |
|
y0 |
|
|
x1 |
|
y1 |
|
5. |
|
|||||||||||||||||||||
1.17 |
x0 |
= 17; |
|
y0 |
= −2; |
x1 = 13; |
|
|
y1 = 4; α = arctg0,75. |
|||||||||||||||||||||||
1.18 |
x0 |
= −6; |
|
y0 |
= 9; |
|
|
x1 |
= 12; |
y1 |
= 8; |
|
α = arccos0,8. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
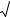
1.19 |
x0 |
= −3; |
y0 |
= −4; |
x1 |
= −7; |
y1 = −5; |
α = 0,5arccos0,64. |
1.20 |
x0 |
= 12; |
y0 |
= 6; |
x1 = 2; y1 |
= 1; α = 2arctg 2. |
||
1.21 |
x0 |
= −7; |
y0 |
= −3; |
x1 |
= −9; |
y1 = −5; |
α = 2arctg0,75. |
|
|
= 0,6; |
|
= 0,1; |
x1 = 1,4; |
|
= 1; |
α = arctg3 |
|
|
||||||
1.22 |
x0 |
y0 |
y1 |
7. |
||||||||||||
1.23 |
x |
|
= −0,3; |
y |
|
= 0,2; |
x |
= 5; |
y |
|
= 3; |
α = arctg |
4 |
. |
||
0 |
0 |
1 |
|
|||||||||||||
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1.24 |
x0 |
= 2,1; |
y0 |
= −1,1; |
x1 |
= 3,1; |
y1 |
= 0,1; α = 2arctg1,5. |
||||||||
1.25 |
x0 |
= 3,2; |
y0 |
= −0,2; |
x1 |
= 1,2; |
y1 |
= −0,8; α = arcsin0,6. |
||||||||
5
РАСЧЁТНОЕ ЗАДАНИЕ 2
Матрица |
А задает |
переход |
от |
базиса |
x1 , |
x2 , |
x3 |
к |
базису |
||||||
y1 , y2 , |
y3 , |
а |
матрица |
В – |
переход |
от |
y1 , |
y2 , |
y3 |
к |
базису |
||||
z1 , z2 , |
z3 . Найти матрицу перехода от |
y1 , |
y2 , |
y3 |
к x1 , |
x2 , x3 |
|||||||||
и матрицу перехода от z1 , |
z2 , z3 |
к x1 , |
x2 , |
x3 . |
|
|
|
|
|||||||
|
|
−1 |
7 |
2 |
|
1 |
1 |
1 |
|
|
|
||||
|
|
|
−10 |
|
|
|
B = |
|
|
|
|
|
|
|
|
2.1 |
A = |
1 |
2 |
, |
2 |
|
0 |
− 3 . |
|
|
|
||||
|
|
|
−1 |
7 |
− 7 |
|
|
|
|
0 |
− 5 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
||||||
9
2.2A = 4
10
13
2.3A = 35
8
2.4A = 13
0
− 2
2.5A = 91
− 5
2.6A = − 2
−11
1 |
3 |
|
2 1 |
0 |
|
||
− 8 |
|
|
|
|
|
|
|
9 , B = 1 |
0 |
3 . |
|||||
− 7 |
3 |
|
|
0 |
5 |
−1 |
|
|
|
|
|
|
|
|
|
4 |
− 6 |
|
10 |
|
9 |
|
0 |
|||
|
|
|
|
|
|
|
|
− 2 |
|
|
−1 6 , |
B = 1 |
|
|
−1 . |
||||||
9 |
− 5 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
4 |
|||||
−1 |
0 |
|
|
|
|
2 |
|
4 |
9 |
|
|
|
|
|
B = |
|
|
|
|
|
|
8 − 7 , |
0 7 |
3 . |
||||||||
5 |
|
|
|
|
|
9 |
|
0 |
7 |
|
−12 |
|
|
|
|
|
|||||
− 7 |
3 |
|
|
1 |
|
1 |
|
−1 |
||
|
|
|
|
B = |
|
|
|
−1 |
|
|
− 3 4 , |
0 |
|
|
2 . |
||||||
− 2 |
−1 |
|
|
|
1 |
|
7 |
|
1 |
|
− 7 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
1 |
8 |
|
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
− 8 5 , B = |
10 0 |
|
3 . |
|||||||
0 |
− 7 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
0 |
|||||
6
− 8
2.7A = 3
10
5
2.8A = 18
9
2.9A = 7
1
11
2.10A = 67
8
2.11A = 8
12
− 6
2.12 A = − 5
− 3
−11 |
− 4 |
|
8 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
10 |
6 , B = 0 |
2 |
7 . |
||||
9 |
0 |
|
|
1 |
4 |
3 |
|
|
|
|
|||||
0 |
− 6 |
|
|
2 |
0 |
|
17 |
|
||
|
− |
|
|
|
|
|
|
|
|
|
2 |
4 , B = 1 0 |
|
3 . |
|||||||
− 3 |
− |
4 |
|
|
|
3 |
4 |
|
2 |
|
|
|
|
|
|
||||||
−1 |
4 |
|
|
0 |
|
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 3 1 , |
B = 1 |
6 |
7 . |
|
||||||
1 |
4 |
|
|
|
1 |
|
0 |
2 |
|
|
|
|
|
|
|
|
|||||
−1 |
5 |
1 |
3 |
6 |
|
||
|
|
|
|
|
|
|
|
− 5 6 , |
B = 0 |
5 2 . |
|||||
− 5 −1 |
|
2 |
−1 0 |
|
|||
|
|
|
|
|
|
|
|
11 |
2 |
4 |
3 |
1 |
|
||
|
|
|
|
|
|
|
|
3 − 3 , |
B = 3 |
2 |
0 . |
||||
9 |
|
|
|
0 |
1 |
|
|
7 |
− 6 |
|
|||||
− 7 |
8 |
|
0 |
1 |
10 |
||
2 − |
|
|
|
|
|
|
|
3 , B = |
1 |
3 |
6 . |
||||
− 3 |
− |
|
|
|
0 |
|
|
1 |
|
3 |
1 |
||||
1 |
3 |
− 7 |
3 |
− 2 |
1 |
||||
|
|
|
− 2 |
|
|
− 2 1 |
|
|
|
2.13 A = 4 5 |
, B = |
3 |
. |
||||||
|
5 |
6 |
− 5 |
|
|
2 |
0 |
− 2 |
|
|
|
|
|
||||||
7 |
0 |
− 2 |
− 5 |
1 |
1 |
||||
|
|
|
|
|
|
|
|
|
|
2.14 A = 4 |
6 |
1 |
, B = 2 |
1 |
0 |
. |
|||
|
− 2 |
1 |
− 3 |
|
|
−1 |
−1 1 |
|
|
|
|
|
|
||||||
7
|
0 |
5 |
− 2 |
|
1 |
3 |
− 2 |
|||
|
|
− 7 |
|
− 5 |
|
|
|
|
|
|
2.15 |
A = |
4 |
, B = |
10 |
0 |
5 . |
||||
|
|
0 |
9 |
−13 |
|
|
|
2 |
0 |
|
|
|
|
|
3 |
|
|||||
|
− 8 |
0 |
3 |
|
1 3 |
− 6 |
|
|||
|
|
− 7 |
|
|
|
|
|
|
|
|
2.16 |
A = |
5 |
8 , |
B = 5 |
3 |
2 . |
|
|||
|
|
−1 |
4 |
|
|
|
|
3 |
|
|
|
|
3 |
|
2 0 |
|
|
||||
2
2.17A = 100
6
2.18A = 4
4
6
2.19A = 40
5
2.20A = 12
5
− 9
2.21 A = −1
− 3
11
2.22 A = 13
14
− 2 |
|
− 8 |
|
1 |
1 |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
− 4 − 2 , B = 1 |
0 4 . |
|||||||||
− 3 |
|
|
|
|
|
3 |
1 |
0 |
|
|
|
− 6 |
|
|
|
|
|||||
− 8 − 5 |
|
−17 |
|
1 0 |
||||||
|
|
|
|
B = |
|
−1 |
|
|
|
|
− 7 − 6 , |
|
|
1 1 . |
|||||||
− 9 |
|
1 |
|
|
|
6 |
|
0 |
1 |
|
|
|
|
|
|
|
|||||
12 |
4 |
|
2 |
|
14 |
|
3 |
|
||
|
|
|
|
|
|
−10 |
|
|
||
6 2 , |
B = 2 |
|
0 . |
|
||||||
2 |
9 |
|
|
|
|
13 |
|
|
|
|
|
|
1 |
|
|
1 |
|
||||
3 |
|
1 |
|
3 |
− 2 |
|
4 |
|||
|
|
|
|
|
|
|
|
|
|
|
10 − 4 , B = |
10 |
|
3 |
|
1 . |
|||||
− 3 |
|
1 |
|
|
|
2 |
−10 |
|
|
|
|
|
|
|
|
0 |
|||||
− 6 |
− 3 |
|
3 |
10 |
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
− 7 2 , B = 3 |
0 |
1 . |
||||||||
5 |
|
|
|
|
|
1 |
− |
|
||
|
1 |
|
5 |
6 |
||||||
2 |
0 |
|
− 2 |
1 |
|
3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
9 1 , |
B = 7 3 |
|
2 . |
|
||||||
6 |
7 |
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
3 |
|
|
||||
8
|
12 6 |
− 2 |
|
6 2 |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
2.23 |
A = 6 1 |
−11 , |
B = 2 |
0 |
2 . |
|
||||
|
|
−1 8 |
|
|
|
|
|
5 |
|
|
|
|
− 5 |
|
5 3 |
|
|
||||
|
−10 |
4 − 6 |
|
2 |
−1 10 |
|||||
|
|
|
− 7 |
− 9 |
|
|
|
|
|
|
2.24 |
A = |
0 |
, B = |
2 |
5 |
0 |
. |
|||
|
|
1 |
0 |
4 |
|
|
|
0 − 2 |
|
|
|
|
|
|
3 |
|
|||||
14 7 |
− 7 |
2 |
−1 |
0 |
|||||
|
|
− 8 |
|
|
|
|
− 2 |
|
|
2.25 A = 14 |
0 |
, B = 1 |
5 |
. |
|||||
|
7 |
1 |
0 |
|
|
0 |
2 |
4 |
|
|
|
|
|
||||||
9
РАСЧЁТНОЕ ЗАДАНИЕ 3
Привести к канонической форме матрицу и найти базис преобразования.
7 |
|
−12 |
− 2 |
|||
|
|
|
− 4 |
|
|
|
3.1 3 |
|
0 . |
||||
|
− 2 |
|
0 |
− 2 |
|
|
|
|
|
||||
2 |
|
0 |
|
0 |
|
|
|
−1 |
|
|
|
|
|
3.3 |
17 |
|
6 . |
|
||
|
3 |
|
6 |
|
|
|
|
|
|
8 |
|
||
|
2 |
19 |
|
30 |
|
|
|
|
− 5 |
|
|
|
|
3.5 0 |
−12 . |
|||||
|
0 |
2 |
|
|
|
|
|
|
5 |
|
|||
−1 |
− 2 |
12 |
|
|||
|
|
|
|
|
|
|
3.7 0 |
|
4 |
|
3 . |
|
|
|
0 |
|
5 |
|
|
|
|
|
|
6 |
|
||
1 |
8 |
23 |
|
|||
|
|
|
|
|
|
|
3.9 0 |
5 |
|
7 . |
|
||
|
0 |
3 |
|
1 |
|
|
|
|
|
|
|||
1 |
−1 |
16 |
|
|||
|
|
|
|
|
|
|
3.11 0 |
1 |
|
−1 . |
|
||
|
0 |
1 |
|
|
|
|
|
|
3 |
|
|||
5 |
9 |
|
7 |
|
||
|
|
|
|
|
|
|
3.13 0 |
3 |
− 2 . |
|
|||
|
0 |
2 |
|
|
|
|
|
|
−1 |
|
|||
9 |
22 |
− 6 |
|||
|
−1 |
− 4 |
|
|
|
3.2 |
1 . |
||||
|
8 |
16 |
|
|
|
|
− 5 |
||||
|
2 |
6 |
5 |
|
|
|
|
|
|
|
|
3.4 0 |
3 |
1 . |
|||
|
0 − 4 |
−1 |
|
||
|
|
|
|
|
|
− 3 |
2 |
0 |
|
||
|
− 2 |
|
|
|
|
3.6 |
1 |
0 . |
|||
|
15 |
− 7 |
|
|
|
|
4 |
|
|||
5 |
− 7 |
0 |
|
||
|
− 3 |
|
|
|
|
3.8 |
1 |
0 |
. |
||
|
16 |
6 |
|
|
|
|
− 3 |
||||
|
|
4 |
0 |
5 |
|
|
|
|
− 2 |
|
|
3.10 7 |
9 . |
||||
|
|
3 |
0 |
|
|
|
|
6 |
|
||
|
− 3 |
11 |
7 |
|
|
|
|
|
|
|
|
3.12 0 |
5 |
− 4 . |
|||
|
|
0 |
1 |
1 |
|
|
|
|
|||
|
5 |
0 |
21 |
|
|
|
|
|
|
|
|
3.14 21 |
2 |
6 . |
|||
|
|
1 |
0 |
|
|
|
|
1 |
|
||
10
