Основные соотношения передач со смещением

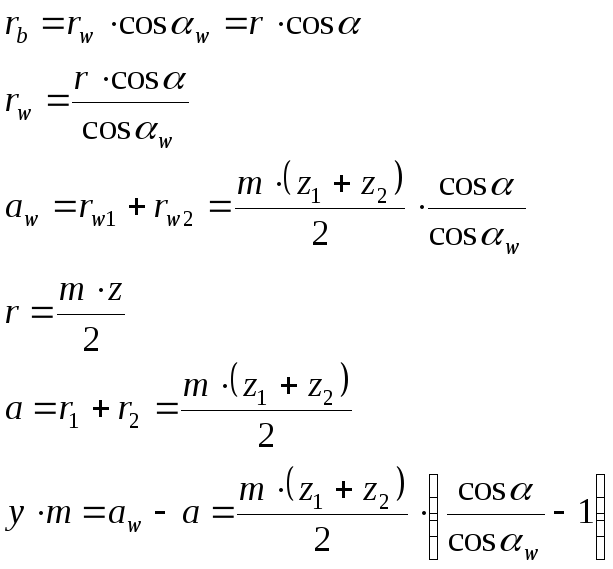
Толщина зуба по начальной окружности равна:

Из условия беззазорного зацепления толщина зуба по начальной окружности одного колеса равна ширине впадины другого колеса.

Радиусы делительных окружностей колес

Радиусы основных окружностей

Начальные радиусы колес

Радиусы окружностей впадин колес

Радиусы окружностей вершин колес

, где толщина зуба по окружности вершин.

Смещение

Коэффициент воспринимаемого смещения

Коэффициент уравнительного смещения

Построение переходной кривой ножки зуба

Зубчатые механизмы

Простые зубчатые механизмы

внешнее зацепление внутреннее зацепление

Там, где присутствует только два колеса, называется простыми зубчатыми механизмами. То, что меньше, называется шестерней; то, что больше - колесом.

Для всех передач внешнего зацепления знак «–», для внутреннего – знак «+».

Сложные зубчатые механизмы

Сложные механизмы, механизмы, в которых присутствует более двух колес.

Последовательное зацепление

Ступенчатые или параллельные соединения

Планетарные передачи

Планетарные передачи – передачи в которых есть зубчатые колеса с перемещающимися в пространстве осями.

Механизмы, имеющие в своем составе зубчатые колеса с перемещающимися в пространстве осями, называются планетарные механизмы.

–центральные (солнечные) колёса (оси расположены на главной центральной оси)

–сатилиты

1) дифференциальный механизм (w = 2) – все колёса вращаются

2) планетарный механизм (w = 1) – хотя бы 1 колёсо закреплено

W = 3n – 2Pn – Pв

n=4; Pn=4; Pв=2

Теорема Виллиса

Если всем звеньям мысленно сообщить угловую скорость относительно главной центральной оси равной по модулю и противоположной скорости водила, то планетарный механизм переходит в обычный сложный зубчатый механизм, такие механизмы получили названия обращённый механизм.

Передаточное отношение

Пример: пусть

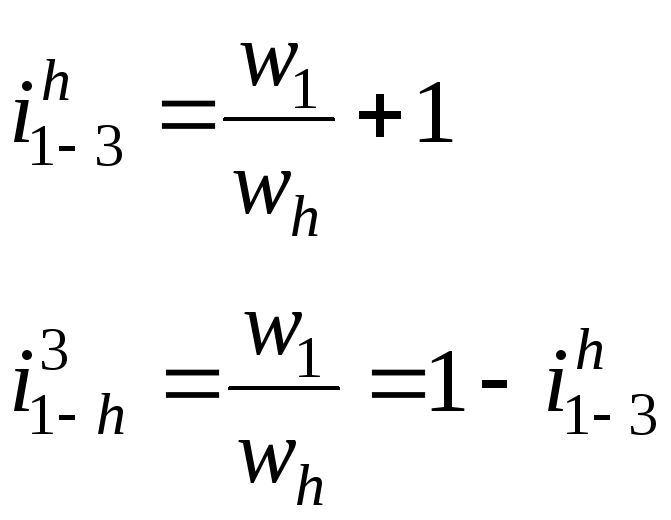
–обращённый механизм

Дифференциальный механизм

Дифференциальный механизм – механизм с двумя степенями свободы.

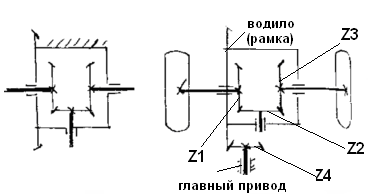
Графическое решение планетарных механизмов

Механизм вычерчивается в масштабе

Правило синтеза планетарных механизмов:

1. Обеспечение заданного передаточного отношения

2. Обеспечение приемлемого КПД

3. Механизм проецируется по условию соосности (на одной оси 2 главных колеса и водило)

а) Схема Джеймса

б)

в)

4) Условие соседства

Где К-число сателлитов

СС_о=2(r₁+r₂)sin(180/K)=m(z₁+z₂)sin(180/K)

CC_o>2r_a2

2r_a2=2(mz₂/2+m)=m(z₂+2)

(z₁+z₂)sin180/K>(z₂+2)

5) Условие сборки

χ₁= χ₂= χ

z₁/K- χ=Q₁

z₃/K+ χ=Q₂

(z₁+z₂)/K=Q

Z_min=17

Z₃-Z₂>8

Z₃>85

Передачи Новикова

Выпуклые профили зубьев одного из колёс, очерченные по дуге окружности, контактируют c вогнутыми профилями другого.

Волновые передачи

Волновая передача состоит из:

1. жёсткого зубчатого колеса - b

2. гибкого зубчатого колеса - g

3. генератора волн

4. роликов

При вращении генератора - 3, благодаря разнице чисел зубьев жёсткого и гибкого колёс, приводится во вращение колесо 2

Z_b-Z_d=K_zU

U- число волн генератора

K_z=1,(2)

I^d_b-h=1-i^h_b-d=1-(Z_b/Z_d)

I^d_b-h=(Z_d-Z_b)/Z_d

∆Z=Z_b-Z_d

m=1; d_b=200мм

Z_b=md_b=200

Z_d=200-2=198

I^d_b-h=-2/198=-1/99

I^d_h-b=1/i^d_b-h=-99

Достоинства волновых передач:

1. 40% зубьев задействованы в передаче нагрузки.

2. Плавность и бесшумность.

3. Большая нагрузочная способность.

Недостатки:

1. U_min=80

2. Сборка и точность изготовления.