17.4. Градиент

Рассмотрим функцию , дифференцируемую всюду на области определения .

Определение 16. Градиентом функции в точке называют -мерный вектор, координаты которого равны значениям частных производных в точке : .

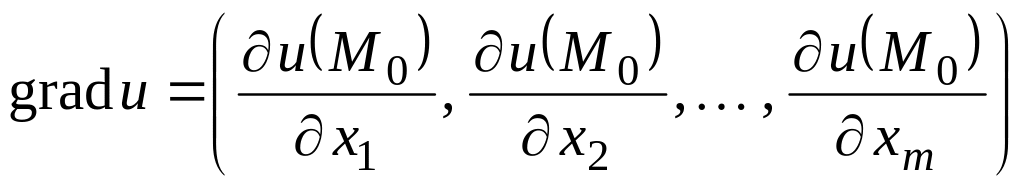Замечание 1. Градиент функции характеризует направление и величину максимальной скорости возрастания этой функции в точке .

Замечание 2. Градиент функции двух переменных в точке – это двумерный вектор .

Теорема 3. Пусть функция дифференцируема всюду на области определения . Тогда градиент функции в точке перпендикулярен линии уровня функции , проходящей через эту точку.

Пример 5. Найти градиент функции в точке .

Решение. 1) Найдем частные производные функции :

, .

2) Вычислим значения частных производных в точке :

, .

3) Составим из полученных значений градиент

.

17.5. Частные производные высших порядков

Пусть функция дифференцируема всюду на области определения . Тогда всюду на множестве у нее существуют частные производные по обеим переменным, которые также представляют собой функции переменных и .

Определение 17. Частными производными второго порядка функции двух переменных в точке называют величины

, , , .

Частные производные, в которых дифференцирование производится по разным переменным, называют смешанными.

Пример 6. Найти все частные производные второго порядка функции .

Решение. 1) Найдем частные производные первого порядка:

, (см. пример 4).

2) Найдем частные производные второго порядка:

, ,

, .

Теорема 4. Если функция в точке имеет непрерывные частные производные до второго порядка включительно, то ее смешанные производные в этой точке равны.

17.6. Применение частных производных в экономике

Частные производные функций многих переменных характеризуют предельные показатели экономических величин.

Пусть – производственная функция; тогда

а) и – эластичности продукции по факторам производства (затратам капитала и труда соответственно);

б) и – эластичности замещения одного ресурса другим, характеризующие необходимое изменение (как правило, в процентах) величины одного ресурса при изменении количества другого ресурса на 1 % с тем, чтобы выпуск при этом не изменился.

Пусть – функция полезности от двух приобретенных товаров и , тогда

а) , – эластичности замещения одного товара другим, характеризующие необходимое изменение (как правило, в процентах) величины одного блага при изменении количества другого блага на 1 % с тем, чтобы полезность при этом осталась неизменной;

б) , – предельные полезности товаров и (если измерять количество товара в стоимостном выражении, то предельные полезности можно рассматривать как функции спроса на соответствующий товар).

Пусть – функция спроса в зависимости от цены товара и доходов потребителей , тогда и – соответственно частичные эластичности спроса от цены и спроса от доходов. Например, в экономике установлено, что для качественных товаров и для низкосортных, так как с ростом доходов спрос на качественные товары увеличивается, а на низкосортные – уменьшается.

Если при исследовании спроса одного товара с ценой рассматривать влияние другого, альтернативного товара с функцией спроса с ценой , то величины ( ) называют перекрестными коэффициентами эластичности спроса. Они показывают приближенно процентное изменение спроса на -й товар при изменении цены альтернативного, -го товара на 1 %. В экономическом анализе показано, что для взаимозаменяемых товаров , так как увеличение цены одного товара приводит к увеличению спроса на другой. В то же время для взаимодополняющих товаров , так как рост цены любого товара приводит к снижению спроса.

В экономическом анализе также показано, что действие эффекта замены и эффекта дохода связано с результирующим изменением спроса следующим уравнением:

, ( ), (17.1)

которое было опубликовано российским математиком Е.Е. Слуцким в 1915 году (и может быть обобщено на любое число переменных). Величина описывает действие эффекта замены (индекс показывает, что перекрестная частная производная рассчитывается при необходимой для поддержания прежнего уровня благосостояния компенсации дохода). Величина описывает действие эффекта дохода, выраженное в тех же единицах, что и эффект замещения (множитель приводит их к одной размерности). Величина представляет собой результирующее воздействие на спрос, складывающееся из изменения структуры спроса и общего его изменения при изменении уровня реального дохода. Уравнение Слуцкого (17.1) может использоваться для расчета эффекта замены и оценки взаимозаменяемости и взаимодополняемости товаров, так как частные производные и вычислить значительно легче, чем . Например, если окажется, что , но  , то товары и взаимозаменяемы, но представляются взаимодополняемыми без учета компенсации. Если , но , то -й товар является худшим (малоценным) по сравнению с -м товаром.

Теоретический материал: [1, гл. 15], [2, гл. 8], [3, гл. 8], [5], [8], [9, гл. 7–11], [10], [11, гл. 5, 6], [12, гл. 9], [17], [19], [20], [21], [27], [33, ч. 1, гл. 8], [40, т. 1, гл. 8, 9].