Задания для решения на практическом занятии
1. Найти и построить область определения функции:
а)
,
б)
,
в)
,
г)
,
д)
,
е)
.
2. Построить линии уровня функции:
а)
,
б)
,
в)
,
г)
,
д)
,
е)
.
3. Найти частные производные первого порядка:
а)
,
б)
,
в)
,
г)
,
д)
,
е) 
,
ж) 
,
з)
,
и)
,
к) 
.
4. Найти градиент функции в указанной точке:
а)
,
;
б)
,
;
в)
,
;
г) 
,
.
5. Найти все частные производные второго порядка:
а)
,
б)
,
в)
,
г)
,
д) 
,
е)
,
ж)
,
з)
,
и)
,
к) 
,
л)
.
6. Найти предельные показатели продукции
при изменении одного из факторов по
функции Кобба–Дугласа
.
7. Найти предельные полезности для
функции
.
8. Функция спроса на товар зависит от
его цены
и дохода потребителя
следующим образом:
.
Используя уравнение Слуцкого, рассчитать
.
Задания для самостоятельной работы
1. Найти и построить область определения функции:
а)
,
б)
,
в)
,
г)
.
2. Построить линии уровня функции:
а)
,
б)
,
в)
,
г)
.
3. Найти частные производные первого порядка:
а)
,
б)
,
в)
,
г)
,
д)
,
е) 
,
ж)
,
з)
,
и)
.
4. Найти градиент функции в указанной точке:
а)
,
;
б)
,
;
в)
,
.
5. Найти все частные производные второго порядка:
а)
,
б)
,
в)
,
г)
,
д)
.
Тема 18. Экстремумы функций многих переменных
18.1. Локальный экстремум функции двух переменных
Рассмотрим
функцию
и точку
.
Определение
1. Если в
некоторой окрестности точки
выполняется
неравенство
,
то точку
называют точкой
локального минимума функции
.
Определение
2. Если в
некоторой окрестности точки
выполняется
неравенство
,
то точку
называют точкой
локального минимума функции
.
Определение 3. Точки локального максимума и локального минимума называют точками локального экстремума.
Теорема
1 (необходимое условие локального
экстремума). Пусть
функция
определена
в некоторой окрестности точки
и имеет в этой точке конечные частные
производные. Если точка
является
точкой локального экстремума функции
,
то значения частных производных в этой
точке равны нулю:
.
Определение 4. Точку области определения функции, в которой , называют стационарной.
Теорема 2 (достаточные условия существования локального экстремума). Пусть функция в некоторой окрестности стационарной точки имеет непрерывные частные производные до второго порядка включительно. Тогда
1)
если
,
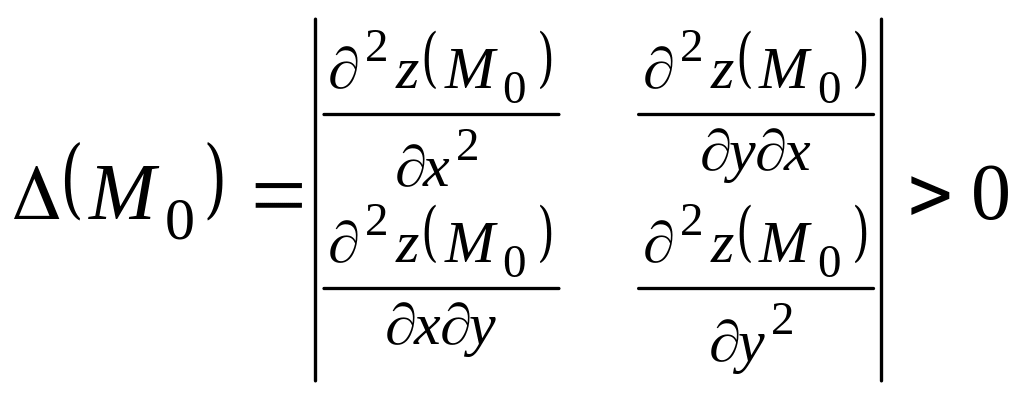то в точке
функция имеет локальный экстремум,
причем, если
,
то точка
является точкой локального минимума,
а если
,
то точка
является точкой локального максимума;
2)
если
,
то в точке
нет
экстремума;
3)
если
,
то задача требует дополнительного
исследования.
Алгоритм исследования функции двух переменных на локальный экстремум
1)
Найти
частные производные первого порядка
функции
:
,
.
2)
Найти
стационарные точки функции как решения
системы уравнений
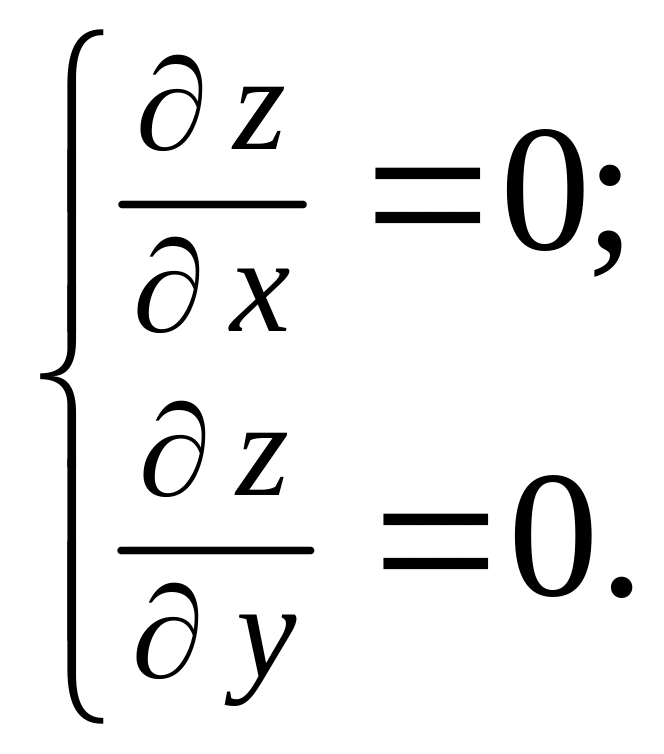
3)
Найти все частные производные второго
порядка
,
,
,
,
составить
определитель
.
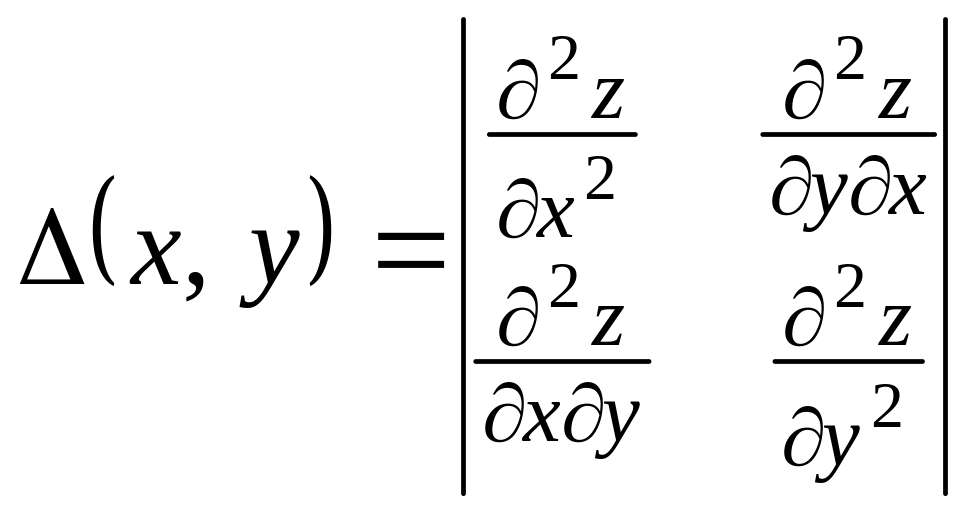4)
Вычислить значения определителя
во всех стационарных точках. Применить
теорему 2.
5) Вычислить значения функции в точках локального экстремума. Записать ответ.
Пример 1.
Найти
точки локального экстремума функции
.
Решение. 1) Найдем частные производные первого порядка:
,
.
2) Найдем стационарные точки функции:
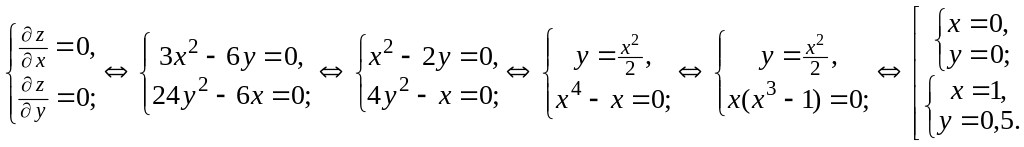
Таким
образом, стационарные точки:
,
.
3)
Вычислим частные производные второго
порядка:
,
,
,
.
Тогда определитель примет вид
.
4)
Вычислим значения определителя в
стационарных точках. В точке
,
следовательно, в точке
нет локального экстремума. В точке
,
следовательно, в точке
есть локальный экстремум. Так как
,
то точка
– точка локального минимума.
5) Вычислим значение функции в точке :
.
Таким
образом, точка локального минимума
,
.