
Основы механики разрушения
.pdf
Рис.6. Система координат и компоненты напряжений у кончика трещины.
Для модели I при плоском напряженном состоянии.
σστ
x
y
xy
=
|
|
|
θ |
|
1 − sin |
|
|
cos |
2 |
|
|||
1 |
|
|
|
|
|
|
|
|
θ |
|
1 + sin |
||
2 π r |
K Ι cos |
2 |
|
|||
|
|
|
|
θ |
||
|
|
cos |
θ |
|||
|
|
2 |
sin |
2 |
||
|
|
|
|
|
||
θ |
sin |
3 |
2 |
|
2 |
θ |
sin |
3 |
2 |
|
2 |
cos 32 θ
θ |
|
|
|
|
|
|
|
|
θ |
|
|
|
|
|
|
|
(11) |
|
|
|
|
|
|
|
|
|
При плоской деформации, когда отсутствуют перемещения по оси Z, напряжения σZ имеют вид:
σ z = μ(σ x +σ y )
Для моделей II и III напряжения определяются по уравнениям типа (11) с заменой КI на КII или КIII и введением своих функций угла θ. Поскольку на продолжении трещины ( θ = 0 ) по уравнению (11) f(К)= I, то выражения для σ X и σY принимает вид:
σx =σy = |
KΙ |
|
2π r |
||
|
При известных компонентах σ и τ могут быть определены главные напряжения в вершине трещины σ1, σ2, σ3. Для тонкой пластины при θ = 0
σ1 = σ y σ2 =σx σ3 =σz = 0
Используя (11) и обобщенный закон Гука можно установить деформации в вершине трещины ex , ey , ez ,γ xy ,γ yz ,γ zx .
Из этого анализа следует, |
что напряжения σ X ,σY ,σz ,τху,τyz,τzx |
||||
1 |
1 |
|
|||
пропорциональны отношению |
|
|
, а деформации пропорциональны |
|
т.е. |
rnσ |
|
r ne |
|||
11

σx ,σ y ,σz ,τxy ,τ yz ,τzx ~ |
|
1 |
|
||
|
r nσ |
|
|||
|
|
|
|||
|
|
1 |
|
|
|
ex ,ey ,ez ,γ xy ,γ yz ,γ zx ~ |
|
|
|
||
r |
nb |
|
|
||
|
|
|
|
||
где nσ = ne= 2I .
Если осуществить интегрирование деформаций ех, еу, еz вершины трещины r, то можно получить перемещения соответственно в направлении осей X,у,Z.
U |
|
|
2(1 + μ) |
r |
f |
x |
(θ) |
|
|
|
|
|
|
|
|||
V |
|
= |
E |
KΙ 2π |
f y (θ) |
|||
|
|
|
|
|
|
f |
|
|
W |
|
|
|
|
|
z |
(θ) |
|
|
|
|
|
|
|
|||
(12)
вокрестности
U, V , W
(13)
Для модели I наибольшие перемещения возникают в направлении оси у,
где действуют наибольшие σ и, как правило, под перемещением берегов
трещины |
понимаются перемещения |
|
V на продолжении |
трещины |
(θ = 0 ; |
f (θ)= I ). Тогда выражения для перемещения V принимают вид: |
|||
|
V = 2(1 + μ) |
KΙ |
r |
(14) |
|
E |
|
2π |
|
На основе (10-14) напряженное и деформированное состояние в вершине трещины полностью определяется коэффициентами, интенсивности напряжений КI, КII, КIII. Для пластин бесконечных размеров при номинальных напряжениях
σ (модель I) и τ (модели II, III) величины коэффициентов интенсивностей напряжений на основе решения задач теории упругости равны:
KΙ |
|
|
σ |
|
|
|
= |
|
|
KΙΙ |
πl τ |
(15) |
||
|
|
|
|
|
|
|
|||
KΙΙΙ |
|
τ |
|
|
12

Для других случаев нагружения, других размерах трещин и конечных размерах в пластик (15) вводятся поправочные функции соответственно fIk, fIIk, fIIIk.
KΙ |
|
|
σ fΙK |
|
|
|
|
= |
|
|
|
KΙΙ |
πl τ fΙΙK |
||||
|
|
|
|
|
|
KΙΙΙ |
|
τ fΙΙΙK |
|||
Поправочные функции определяются на основе решения соответствующих задач или по экспериментальным данным.
Для пластин ограниченных размеров с симметричной центральной трещиной (рис.7а) поправочную функцию можно приближенно записать:
fΙK ≈ |
2B tg |
πl |
|
πl |
2B |
Для пластины с одной или двумя боковыми трещинами (рис.7б) при
2lb < 0,2
fΙK =1,12 |
2B tg |
πl |
|
πl |
2B |
а) |
б) |
Рис.7.2 Пластины с трещинами
13

Из анализа поведения поправочной функции ξIk при изменении ширины
пластины (рис.8) следует, что трещины одинаковых размеров в телах ограниченных размеров являются более опасными.
Рис.8. Зависимость поправочной функции fIK от ширины пластины
В общем случае нагружения при расчете напряжений используется принцип независимости действия сил:
σx = |
KΙ |
fΙX (θ)fΙK + |
KΙΙ |
fΙΙX (θ)fΙΙK + |
KΙΙΙ |
fΙΙΙX (θ)fΙΙΙK |
|
πl |
|
πl |
|
πl |
|
Аналогично определяются σy,σz,τху.
УПРУГО-ПЛАСТИЧЕСКОЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ
|
СОСТОЯНИЕ В ВЕРШИНЕ ТРЕЩИНЫ. |
|
В связи |
с тем, что напряжения |
σ и деформации е |
в вершине |
трещин малых r в |
соответствии с (18-19) |
достигают больших величин при любых номинальных напряжениях, а пределы текучести σт конечны, то в вершине трещин возникают зоны пластических
деформаций, в которых происходит перераспределение напряжений.
Размер зоны пластических деформаций rт в тонкой пластине можно
определить в I-м приближении из условия σу=σт (Ирвин)(рис.9).
14
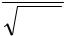
σ |
y |
= |
KΙ = σ |
T |
|
|
2πrT |
||
|
|
|
|
Отсюда
|
|
1 |
|
KΙ 2 |
|
|
rT |
= |
|
|
|
|
(16) |
|
|
|||||
|
|
|
|
|||
|
|
2π |
σT |
|
||
Однако, в связи с тем, что на участке rт передается меньшая сила, чем по
упругому решению (6), нарушаются интегральные условия равновесия. Это приводит к перераспределению напряжений и дополнительной перегрузке при
r > rт.
Ирвин предложил рассматривать не фактическую длину трещины ι, а
условную (фиктивную) длиной ιт=ι+rт, однако, в последующем были
проведены уточнения и получено ιт≈ι+rт/2 |
(17) |
15

Рис. 9. Упругое (5), упруго-пластическое (21) и упруго-пластическое с упрочнением (23) распределение напряжений вблизи фронта трещин
Для бесконечной пластины с центральной трещиной: KΙ =σ π l |
(18) |
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
l |
|
σ |
2 |
|
rT |
= |
|
σ πl |
= |
|
|
(19) |
|||
|
|
|
2 |
|
|
|
||||
|
|
2π |
σT |
|
|
σT |
|
|||
|
|
|
rT |
|
|
|
l |
|
σ |
2 |
||||
lT |
= l + |
|
|
= l + |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||||
2 |
4 |
|
|
|
||||||||||
|
|
|
|
|
σT |
|||||||||
|
|
|
|
|
|
|
σ |
|
|
2 |
|
|||
|
lT = l |
|
|
|
|
|
|
|
|
|
|
|
(20) |
|
|
|
|
σ |
|
|
|||||||||
|
1 |
+ 0,25 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
T |
|
|
|||
Это выражение Q учетом (18) подставляется в (5):
16

KΙ = σ  πlT
πlT
Тогда по Ирвину распределение напряжений в упругой области будет:
σ y = |
K |
Ι |
= |
σ πlT |
= σ |
l |
T |
(21) |
|
2πr |
|
||||||
|
2πr |
|
|
2r |
|
|||
Уравнения (18) — (21) достаточно хорошо описывают распределение σ и
следовательно е для реальных пластин о фиктивной ιт при σ < 0,6σт.
Таким образом был осуществлен переход от упругого решения к упругопластическому.
Более точное решение для идеального упруго-пластического материала получено Леоновым, Панасюком–Дагдейлом (I960-1961). Ими было предложено считать, что пластическая зона имеет узкую клиновидную форму на продолжении трещины, а размер этой зоны не известен. Однако известно,
что напряжения в зоне ρт для идеального, упруго-пластического материала
равны σт (рис.10)
17

Рис.10. Модель Леонова-Панасюка-Дагдейла За пределами этой зоны напряжения будут упругими, поэтому упруго-
пластическая задача сводится к упругой для тела, имеющего трещину, равную ι+ρт и нагруженную:
1- растягивающими напряжениями σ на бесконечности.
2– сжимающими напряжениями ρт в пределах rт.
Решением этих 2-х упругих задач получено, что
|
|
|
πσ |
|
|
|
ρT |
|
|
|
−1 |
(22) |
|
|
|
|||||
= l sec |
|
|
||||
|
|
|
2σT |
|
|
|
Размер пластической зоны (rт, ρт )растет с увеличением напряжений,
причем ρт > rт (рис.11).
Рис.11.Зависимость размера пластической зоны и раскрытия трещины от уровня напряжений.
18

До номинальных напряжений σ/σт= 0,5 ÷ 0,6 (что справедливо при запасах
nт = 0.5 ÷ 2.0) (19) и (22) дают мало отличающиеся результаты. При больших
напряжениях необходимо использовать (22).
Для материалов с упрочнением Хан и Розенфельд (1964г.) предложили вместо
σт в (22) использовать условный предел текучести σ,т.
σT′ = |
σT +σв |
(23) |
|
2 |
|
В вершине трещины по Ирвину и Леонову-Панасюку-Дагдейлу возникает раскрытие трещины (рис.12)
Рис.12. Схема раскрытия трещины:
1- фронт ненагруженной трещины,
2- фронт нагружённой трещины,
δ- раскрытие трещины в вершине за счет образования пластических деформаций.
Если величины rт и ρт подставить вместо V в уравнение (14), то величина раскрытия δбудет равна
19

|
|
δ |
= 2V = |
πσ 2l |
|
|||
|
|
σT E -по Ирвину |
(24) |
|||||
|
8σT l |
|
π |
|
σ |
|
|
|
δ = 2V = |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
πE |
ln sec |
2 |
σT |
- по Леонову-Панасюку-Дагдейлу (25) |
|
|||
|
|
|
|
|
||||
(25) является более общим выражением, т.к.(24) является его 1-м членом разложения в ряд.
Раскрытие трещин δпри увеличении σрастет аналогично rт/ι(рис.11).
Анализ напряжений и деформации в зоне трещины можно выполнить используя теорию концентрации.
Используя упругие решения и понятия о коэффициентах концентрации напряжений в вершине трещины можно записать
|
|
|
σ y = |
|
KΙ |
|
|
|
ασ = |
σ y |
|
|
|
|||||
|
|
|
|
2πr |
|
|
|
σ |
|
|
|
|
||||||
Переходя к относительным напряжениям |
|
|
|
|
|
|
|
|
|
|||||||||
|
σy |
= |
K |
Ι |
= |
σ |
πl |
|
= σ |
|
πl |
= |
K |
T |
||||
|
σT |
|
σT |
|
|
|
|
|
|
|
|
|||||||
|
|
σT 2πr |
|
|
2πr |
|
|
|
2πr |
|
2πr |
|||||||
где |
KT = σ |
|
πl , получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
σmax |
|
σ y |
σT |
|
|
KT |
|
|
|
||||
|
|
|
ασ = |
= |
σ |
|
= |
σ |
|
|
(26) |
|||||||
|
|
|
|
|
σ |
|
σT |
|
|
2πr |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Получить распределение напряжений σ и деформаций е в вершине трещины и
для любой точки X можно через коэффициенты концентраций деформаций Ке и
напряжений Кσ в зависимости от σ= σn. Выделяя из полученных решений
20
