
МЕТОДИЧЕСКИЕ УКАЗАНИЯ по курсу “Основы физики прочности и механики разрушения”
.pdfМинистерство образования и науки Российской Федерации
МАТИ - Российский государственный технологический университет им. К.Э. Циолковского
Кафедра “Механика материалов и конструкций”
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по курсу “Основы физики прочности и механики разрушения”
Составители: Котов П.И. Агамиров Л.В.
Москва 2006
1
ВВЕДЕНИЕ
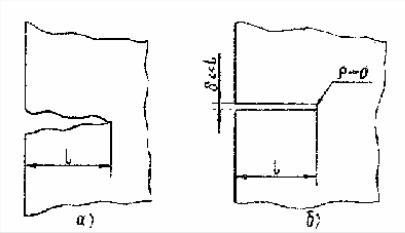
В механика разрушения предполагается наличие в материалах несплошностей, имитирующих начальную или возникающую макродефектность. Причем реальные дефекты (трещины статического и циклического происхождения, расслоения, скопления пор, cвaрочные дефекты, коррозионные трещины и др.), имеющие в общем случае сложную форму (рис. 1-а), представляются в механике разрушения в виде тонких полостей (щелей) с прямыми берегами, один из размеров которых (ширина) существенно меньше двух других (рис. 1-б).
Рис. 1. Реальный дефект - а; его расчетная схема – б
Основой решения задач в механике разрушения является анализ напряженного и деформированного состояния в окрестности вершины трещины.
Впервые такой анализ был выполнен Гриффитсом (1920-1922 г.г.), развит Мусхелишвили (1938-1964 г.г.), Ирвином (1957-1966.г.г.), Райсом (1962-1968 г.г.),
Панасюком-Леоновым (1959-1964 г.г.), Дагдейлом (1962-1964 г.г.), Черепановым, Морозовым, Партоном (1962-1970 г.г.) и другими.
2

1. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ВЕРШИНЕ ТРЕЩИНЫ В УПРУГОЙ СТАДИИ
Моделирование реальных трещин в телах осуществляется с помощью эллиптических надрезов или отверстий, гиперболических надрезов на основе решение задач теории упругости, а также бесконечно острыми щелями на основе функций комплексного переменного.
1.1. Пластины с эллиптической щелью.
На основе решения задачи теории упругости для эллиптического отверстия в пластине наибольшие напряжения в направлении номинальных напряжений σ возникают в вершине отверстия на большой полуоси (рис. 2)
σy max =σασ ,
где σ - номинальные напряжения; |
|
|
|
|
|
|
|||
ασ |
- теоретический коэффициент концентраций напряжений |
|
|||||||
|
По теории упругости для эллипса |
|
|
|
|
||||
|
ασ =1+2 |
l |
ρ |
, |
|
|
(1) |
||
|
|
|
|
|
|
|
|
|
|
тогда |
|
|
|
|
|
|
|
|
|
|
σ |
|
=σ |
1+2 |
|
l |
. |
(2) |
|
|
|
y max |
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
В случае круглого отверстия |
l = ρ;ασ = 3,0. |
|
|
|
|||||
|
Если сохранить постоянным размер отверстия l и уменьшить радиус |
ρ , то при |
|||||||
ρ → 0 |
σ y max → ∞ (рис. 2-б). |
|
|
|
|
|
|
|
|
|
В отличие от обычных |
форм |
концентрации, рассматриваемых |
в теории |
|||||
упругости, в механике разрушения максимальные напряжения оказываются неопределенными по величине - бесконечно большими (сингулярная задача) и это делает неприменимым использование обычных критериев разрушения, общепринятых для сопротивления материалов (например σ1 ≤[σ];σЭКВ ≤[σ]). Такое положение возникает в
пределах упругих решений в силу того, что радиус надреза ρ → 0 . Вместе с тем в
реальных деталях радиусы закругления в вершинах дефектов зависят от технологии изготовления и являются конечными величинами, соизмеримыми с радиусами пор, размерами структурных составляющих и пределе с межатомными расстояниями.
Точное решение задачи о распределении напряжений в пластине на продолжении
трещины (Мусхелишвили, Колосов) приводит к выражению: |
|
||
σy = |
x |
σ. |
(3) |
|
x2 −l 2 |
|
|
3
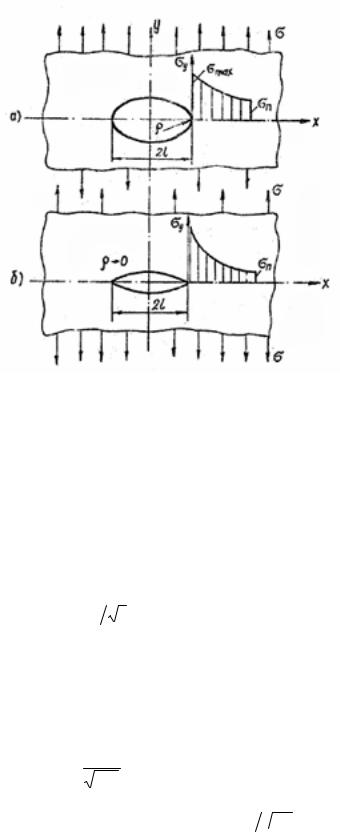
У вершины трещины x →l и по (3) σ y также стремится к бесконечности
(σ y → ∞ ).
Вдали от трещины x → ∞,σ y →σ что соответствует краевым условиям.
Рис. 2. Распределение напряжений в пластине с эллиптическим отверстием:
а) при ρ =const;
б) при ρ → 0
Для бесконечно большого числа сочетаний длин и формы трещин, размеров тел и способов нагружения необходимо получать свои решения типа (3).
Обобщая полученные решения, Ирвин (1957 г.) показал, что характер распределения напряжений σ y в упругом теле у вершины трещины, независимо от ее
размеров, ориентации и способа нагружения при r<0,05l , одинаков и подчиняется закону
σ y ~ 1 r , |
(4) |
где: r=x-l - расстояние от вершины трещины.
Таким образом для описания распределения σ y необходимо знать только
коэффициент пропорциональности в выражении (4).
По предложению Ирвина (4) записывается в форме
σ y = |
K . |
(5) |
|
2πr |
|
Коэффициент пропорциональности получился равным K  2π .
2π .
Коэффициент K характеризует распределение напряжений у вершины трещины и является основный параметром напряженного состояния. В силу фундаментальности уравнения (5) этому коэффициенту дано специальное название: коэффициент
4
интенсивности напряжений. При установленном распределении напряжений σ y для заданного расстояния r на основе (5):
K =σ y  2πr.
2πr.
Коэффициент интенсивности напряжений K в отличие от теоретического коэффициента концентрации напряжений имеет размерность
[K ]= [σ][ r ]= МПа
r ]= МПа м;кг/ мм3 / 2 .
м;кг/ мм3 / 2 .
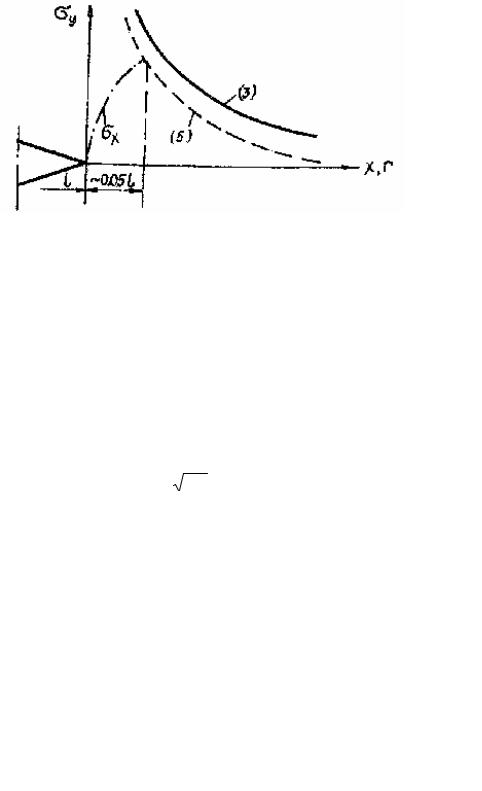
Выражения (3) и (5) дают сопоставимые результаты для σ y при малых значениях
r (рис. 3).
Поскольку уравнение (5) для больших значений r дает меньшие величины σ y по
сравнению с точным решением (3), то оно может быть использовано только для определения местных напряжений непосредственно у вершины трещины.
Для конечных значений ρ , наоборот, точное, решение (3) дает
удовлетворительное описание распределения напряжений в области больших r .Это совпадение имеет место при r>0,25 ρ .
Для тонких пластин с трещинами, когда при нагружении в области у кончика
трещины возникает |
плоское напряженное состояние, напряжения σx |
и σ y |
в этой зоне оказываются сопоставимыми по величине. |
σx =0. С |
|
Для радиусов |
ρ конечной величины вточке А (рис. 2-а) напряжения |
|
увеличением r напряжения σx сначала возрастают, а затем убывают и описываются уравнением (5).
Формулы (3) в (5) дают совпадающие до 3% величины σ y при |
r / l ≤ 0,08. |
||
Для r / l < 0,08 при известных r и σ y на основании (5) имеем |
|
|
|
|
K =σ y 2πr. |
(6) |
|
Уравнение (6) по известным из эксперимента или расчета σ y и r |
|
|
|
позволяет определить основную величину K. |
|
|
|
|
|
|
|
|
|
|
|
Рис. З. Сопоставление решений Myсхелишвили,
Колосова (3) и Ирвина. (5) в зоне перед кончиком трещины
5
1.2. Метод сечений для приближенного расчета коэффициента интенсивности напряжений.
Одна из основных задач, стоящих перед механикой разрушения в связи с расчетом на прочность, состоит в определении коэффициента интенсивности напряжений.
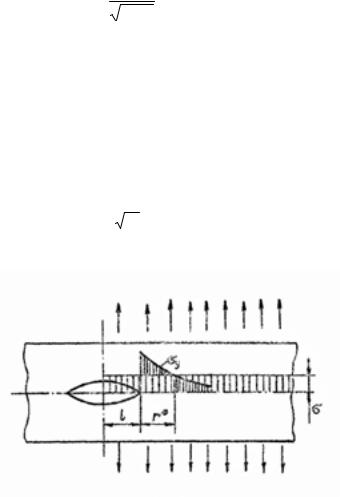
Покажем возможностьпримененияизвестноговстроительноймеханикеметодасеченийдля еговычисления. Рассмотримплоскуюзадачуотрещине. Выделимчастьтелавоображаемымсечением такимобразом, чтобыэтосечениепроходилочерезконецтрещины(рис. 4).
Условие равновесия внешних и внутренних сил по Е. М. Морозову сводится к тому, что усилие, не передающееся через линию трещины, компенсируется дополнительным усилием от концентрации напряжений у вершины трещины.
При образовании трещины длиной 2l усилие, не передающееся через трещину, равно
r*
Ρ = 2lσ , авозросшеенапряжениеуконцовтрещинысоздаетдополнительноеусилие, равное 2∫σy dr.
Отсюда: |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
r* |
|
|
P = 2lσ = 2∫ |
σ y dr. |
(7) |
||||
|
|
|
|
0 |
|
|
Размер r находим из условия |
|
|
|
|||
σ y = |
|
K |
|
=σ, (рис. 4) |
|
|
|
2πr * |
|
|
|||
отсюда |
|
|
|
|
|
|
r* = |
1 |
K |
|
2 |
|
|
|
|
|
. |
|
||
2π |
|
|
||||
|
σ |
|
|
|
||
Подставляя в (7) σ y и |
выполнив интегрирование, находим |
коэффициент |
||||
интенсивности напряжений |
|
|
|
|
|
|
K =σ |
πl , |
|
|
(8) |
||
который совпадает с его точным значением.
Рис. 4. Схема метода сечений.
6
1.3. Деформированное состояние в вершине трещины
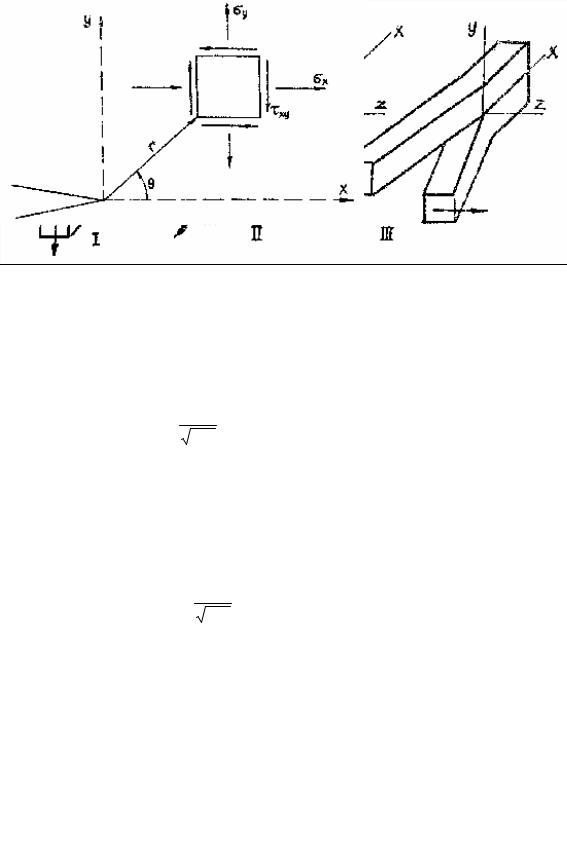
Деформированное состояние в вершине трещина при любых способах нагружения может бытьпредставленокаксуперпозициядеформацийтрехосновныхтиповI, II, III (рис. 5).
Рис. 5. Основные виды деформации трещины: I - трещина нормального отрыва;
II - трещина поперечного (плоского) сдвига;
III - трещина продольного (антиплоского) сдвига
Каждая из моделей характеризуется своей величиной K . Тогда для рассмотренного случая пластины (рис. 2-б)
σ y = |
KI . |
(9) |
|
2πr |
|
Эта формула справедлива для напряжений по оси X.
В соответствии с решениями задач для тел с трещинами в общем случав напряженное состояние определяется тремя параметрами: расстоянием r от
начала координат до рассматриваемой точки, углом θ |
и коэффициентом |
||||
интенсивности напряжений KI, KII или KIII. (рис. 6) |
|
|
|||
|
σx, y,z = |
1 |
[f (KI , KII , KIII ,θ)]. |
(10) |
|
|
|
2πr |
|
|
|
|
|
|
|
|
|
Рис. 6. Система координат и компоненты напряжений у кончика трещины
7

Для модели I при плоском напряженном состоянии
σxσ y =τxy
|
|
θ |
−sin |
θ |
sin |
3 |
θ |
|||||
|
cos |
2 |
1 |
2 |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
θ |
+sin |
θ |
sin |
3 |
θ |
|||||
2πr |
KI cos |
2 |
1 |
2 |
2 |
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
θ |
|
θ |
cos |
3 |
|
|
||||
|
cos |
2 |
sin |
2 |
2 |
θ |
||||||
|
|
|
|
|
|
|
|
|
||||
(11)
При плоской деформации, когда отсутствуют перемещения по |
оси |
Z |
|||||
напряжения σz |
имеют вид: |
|
|
|
|
|
|
|
σz = μ(σx +σ y ). |
|
|
|
|
||
ДлямоделейII иIII напряженияопределяютсяпоуравнениямтипа(II) сзаменой KI на KII |
или |
KIII |
|||||
и введением |
своих функций |
угла |
θ . |
Поскольку на продолжении |
трещины |
||
(θ =0 ) поуравнению(II) f(K)=1, товыражениядля |
σx и σ y принимаютвид: |
|
|
||||
|
σx =σ y = |
KI |
; |
|
|
|
|
|
|
|
2πr |
|
|
|
|
|
τxy = 0. |
|
|
|
|
|
|
При известных компонентах σ |
и |
τ могут быть определены главные напряжения в |
|||||
вершине трещины σ1,σ2 ,σ3 . Для тонкой пластины при θ =0 |
|
|
|||||
σ1 =σ y ;σ2 =σx ;σ3 =σz = 0.
Используя (II) и обобщенный закон Гука, можно установить деформации в вершине
трещины ex ,ey ,ez ,γxy ,γxz ,γ yz .
Из этого анализа следует, что напряжения σx ,σ y ,σz ,τxy ,τxz ,τyz пропорциональны отношению 1 rnσ , а деформации ~ 1
rnσ , а деформации ~ 1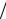 r ne , т.е.
r ne , т.е.
σx ,σ y ,σz ,τxy ,τxz ,τyz ~ |
|
1 |
|
|||
|
|
|
||||
r nσ |
(12) |
|||||
|
1 |
|
|
, |
||
ex ,ey ,ez ,γxy ,γxz ,γ yz ~ |
|
|
|
|
||
r |
ne |
|
|
|
||
|
|
|
|
|
|
|
где nσ = ne =1/ 2.
Если осуществить интегрирование деформаций ex ,ey ,ez в окрестности вершины
трещины по r, то можно получить перемещения U, V, W соответственно в направлении осей X, Y, Z.
U |
|
|
|
|
f |
|
|
|
|
2(1+ μ) |
|
r |
x |
(θ) |
|
||
|
= |
KI |
|
|
(13) |
|||
V |
E |
f y (θ) |
||||||
|
|
|
2π |
|
|
|
|
|
W |
|
|
|
fz |
(θ) |
|
||
8

Для модели I наибольшие перемещения возникают в направления оси Y, где действуют наибольшие σ и, как правило, под перемещением берегов трещины понимаются перемещения V на продолжении трещины (θ = 0; f (θ)=1). Тогда выражения для перемещения V приникают вид:
V = |
2(1+ μ)K |
r . |
(14) |
|
E |
I 2π |
|
На основе (10-14) напряженное и деформированное состояние в вершине трещины полностью определяется коэффициентами интенсивности напряжений KI, КII
КIII. Для пластин бесконечных размеров при номинальных напряжениях σ (модель I) и
τ (модели II,III) величины коэффициентов интенсивностей напряжений на основе решения задач теории упругости равны:
KI |
|
|
σ |
|
|
|
|
= |
|
|
(15) |
KII |
πl τ |
||||
|
|
|
|
|
|
KIII |
|
τ |
|
||
Для других случаев нагружения, других размеров трещин и конечных размеров пластин в (15) вводятся поправочные функции соответственно fIK , fIIK , fIIIK .
KI |
|
|
σ fIK |
|
|
|
|
= |
|
|
|
KII |
πl τ fIIK |
||||
|
|
|
|
|
|
KIII |
|
τ fIIIK |
|||
Поправочные функции определяются на основе решения соответствующих задач или по экспериментальном данным.
Для пластин ограниченных размеров с симметричной центральной трещиной (рис. 7-а) поправочную функцию можно приближенно записать:
|
|
|
fIK |
2B tg |
πl . |
|
|
|
|
|
πl |
2B |
|
Для пластины с |
одной |
или |
двумя |
боковыми трещинами (рис. 7-б) при |
||
l / 2B < 0,2 : fIK =1,12 |
2B tg |
|
πl . |
|
|
|
|
πl |
2B |
|
|
|
|
Рис. 7. Пластины с трещинами
9
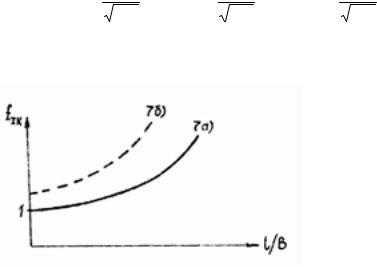
Из анализа поведения поправочной функции fIK при изменении ширины пластины
(рис. 8) следует, что трещины одинаковых размеров в телах ограниченных размеров являются более опасными.
В общем случае нагружения при расчете напряжений используется принцип независимости действия сил
σx = |
KI |
fIX (θ)fIK + |
KII |
fIIX (θ)fIIK + |
KIII |
fIIIX (θ)fIIIK . |
|
2πr |
|
2πr |
|
2πr |
|
Аналогично определяются σ y ,σz ,τxy .
Рис. 8. Зависимость поправочной функции fIK от ширины пластины
10
