
МЕТОДИЧЕСКИЕ УКАЗАНИЯ по курсу “Основы физики прочности и механики разрушения”
.pdf
2.УПРУГОПЛАСТИЧЕСКОЕ НАПРЯЖЕННОДЕФОРМИРОВАННОЕ СОСТОЯНИЕ В ВЕРШИНЕ ТРЕЩИНЫ
В связи о тем; что напряжения σ и деформации e в вершине трещин малых r в соответствий с (18-19) достигают больших величин при любых номинальных напряжениях, а пределы текучести σT конечны, то в вершине трещин возникают зоны
пластических деформаций, в которых происходит перераспределение напряжений. Размер зоны пластических деформаций rT в тонкой пластине можно определить в
1-ом приближении из условия σ y =σT (Ирвин) (рис. 9).
σ y = |
KI |
=σT , |
|
2πrT |
|
отсюда
|
|
1 |
|
KI |
2 |
|
|
rT |
= |
|
|
(16) |
|||
|
|
||||||
|
|
|
. |
||||
|
|
2π |
σT |
|
|||
Однако в связи с тем, что на участке rT передается меньшая сила, чем по упругому решению (6), нарушаются интегральные условия равновесия. Это приводит к перераспределению напряжений и дополнительной перегрузке при r>rT.
Ирвин предложил рассматривать не фактическую длину трещины l, а условную (фиктивную) длину lT=l+rT, однако в последующем были проведены уточнения и получено
lT l +rT 2. |
(17) |
Далее использовано упругое решение.
Рис. 9. Упругое (5), упругопластическое (21), и упругопластическое с упрочнением (23) распределение напряжений вблизи фронта трещин
11

Для бесконечной пластины с центральной трещиной
K I =σ πl , |
(18) |
тогда
r |
= |
1 |
|
σ πl |
2 |
= |
l |
|
σ |
|
2 |
|
|
|
|
|
|
|
|
|
|
, |
|||
T |
|
|
|
σT |
|
|
|
2 |
|
|
|
|
|
|
2π |
|
|
|
|
σT |
|
||||
|
|
|
rT |
|
l |
|
σ |
2 |
|
|
||
lT |
= l + |
=l + |
|
|
. |
|
(19) |
|||||
2 |
4 |
|
σT |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
lT |
= l[1+0,25(σ σT )2 ]. |
|
|
(20) |
||||||||
Это выражение с учетом (18) подставляется в (5)
KI =σ  πlT .
πlT .
Тогда по Ирвину распределение напряжений в упругой области будет
σ y = |
K |
I |
= |
σ πlT |
=σ |
l |
. |
(21) |
|
2πr |
T |
||||||
|
2πr |
|
|
2r |
|
|
||
Уравнения (18) - (21) достаточно |
хорошо |
описывают |
распределение σ и |
|||||
следовательно e для реальных пластан с фиктивной |
lT при σ < 0,6σT . Таким образом |
|||||||
был осуществлен переход от упругого решения к упругопластическому.
Более точное решение для идеального упругопластического материала получено Леоновым-Панасюком-Дагдейлом (I960-I96I). Ими было предложено считать, что пластическая зона имеет узкую клиновидную форму на продолжении трещины, а размер этой зоны не известен. Однако известно, что напряжения в зоне ρT для идеального
упругопластического материала равны σT (рис. 10).
Рис. 10. Модель Леонова-Панасюка-Дагдейла
12

За пределами этой зоны напряжения будут упругими, поэтому упругопластическая задача сводится к упругой для тела, имеющего трещину, равную
l + ρT и нагруженную:
1 - растягивающими напряжениями σ на бесконечности, 2 - сжимающими напряжениями σT в пределах rT .
Решением этих 2-х упругих задач получено, что
|
|
|
πσ |
|
|
|
ρT |
|
|
|
|
−1 . |
(22) |
|
|
|||||
=l sec |
2σT |
|
||||
|
|
|
|
|
|
|
Размерпластическойзоны (rT , ρT ) растетсувеличениемнапряжений, причем ρT > rT |
(рис. 11). |
|||||
Рис. 11. Зависимость размера пластической зоны и раскрытия трещины от уровня напряжений
До номинальных напряжений σ σT 0,5 ÷0,6 (что справедливо при запасах nT =1,5 ÷2,0 ) (19) и (20) дают мало отличающиеся результаты. При больших напряжениях
σT 0,5 ÷0,6 (что справедливо при запасах nT =1,5 ÷2,0 ) (19) и (20) дают мало отличающиеся результаты. При больших напряжениях
необходимоиспользовать(22).
Для материалов с упрочнением Хан и Розельфельц (1964 г.) предложили вместо σT в (22) использовать условный предел текучести σT′ .
σT′ = |
σT +σв |
. |
(23) |
|
2 |
||||
|
|
|
1.2.Раскрытие трещины
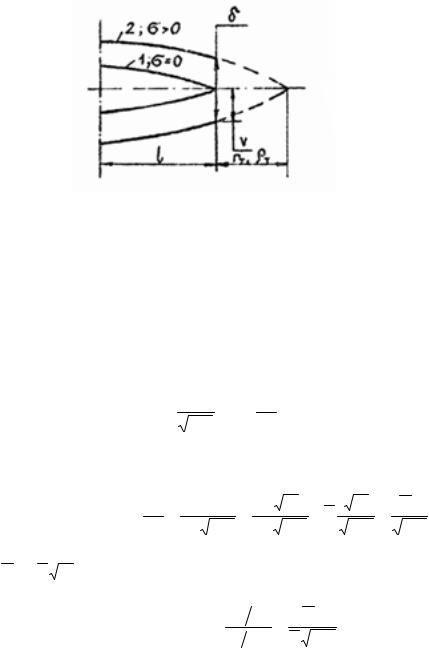
Ввершине трещины по Ирвину и Леонову-Панасюку-Дагдейлу возникает раскрытие трещины (рис. 12).
Если величины rT и |
ρT подставить вместо V |
в уравнение (14), то величина |
|||
раскрытия δ будет равна |
|
|
|
|
|
δ |
= 2V = |
πσ 2l |
- по Ирвину, |
(24) |
|
σT E |
|||||
|
|
|
|
||
13
|
8σT l |
|
|
|
|
δ = 2V = |
π |
σ |
|
|
|
|
|
|
|||
πE |
lnsec 2 σT - |
по Леонову-Панаску-Дагдейлу. (25) |
|||
(25) является более общим выражением, т.к. (24) является его 1-ым членом |
|||||
разложения в ряд. |
δ при увеличении |
σ растет аналогично rT/l (рис. 11). |
|||
Раскрытие трещины |
|||||
Рис.12.Схема раскрытия трещины:
1-фронт ненагруженной трещины;
2-фронт нагруженной трещины;
δ-раскрытие трещины в вершине за счет образования пластических деформаций
Анализ напряжений и деформации в зоне трещины можно выполнить, используя теорию концентрации.
Используя упругие решения и понятия о коэффициентах концентрации напряжений в вершине трещины, можно записать
σ |
y |
= |
K |
I |
;α |
σ |
= |
σy |
. |
|
σ |
||||||||
|
|
2πr |
|
|
|
||||
Переходя к относительным напряжениям
|
|
σy |
= |
|
K |
I |
= |
σ |
πl |
=σ |
πl |
= |
K I |
, |
||||
|
|
σT |
σT |
σT |
|
|
|
|
||||||||||
|
|
|
2πr |
2πr |
2πr |
|
2πr |
|
||||||||||
где |
K I =σ πl , |
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ασ = |
σ |
max |
|
= |
σ y |
σT |
= |
|
K I |
. |
|
|
(26) |
|||
|
|
σ |
σ σT |
σ |
2πr |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Получить распределение напряжений σ |
и деформаций e в вершине трещины и |
||||||||||||||||
для любой точки |
X можно через коэффициенты концентрации деформаций Ke и |
|||||||||||||||||
напряжений Kσ в |
зависимости |
от |
|
|
= |
|
n и |
|
m. Выделяя |
из полученных решений |
||||||||
σ |
σ |
|
||||||||||||||||
постоянные коэффициенты, не зависящие от r, можно получить уравнения типа (5)
14

|
|
|
|
σ y = ( |
K Iσ |
, |
||
|
|
|
|
2πr )nrσ |
||||
|
|
|
|
|
|
K Ie |
(27) (ИМАШ) |
|
|
|
|
|
e y = |
|
, |
||
|
|
|
|
( |
2πr )nre |
|
||
где |
|
Iσ , |
|
Ie - коэффициенты интенсивности напряжений и деформаций в |
||||
K |
K |
|||||||
упругопластической области.
Из этих решений следует, что
2m
K Iσ = K I 1+m ,
2
K Ie = K I 1+m .
Для упругого материала ( m=1)
K Iσ = K Ie = K I .
nre = nrσ =1, тогда (27) сводится к (5).
Для идеально упругопластического материала (m =0)
K Iσ =1; K Ie = K I 2 .
Выражения (28) - (30), при введении в них функции
(28)
(29)
(30)
f (r,θ) пo (II), позволяют
описать конфигурацию и размеры пластических зон в вершине трещины, приближающиеся к точным.
Показатели nrσ и nre |
в (27) соответственно равны: |
|
|||||||||
n |
rσ |
= |
|
2m |
;n |
re |
= |
|
2 |
. |
(31) |
1+m |
|
||||||||||
|
|
|
|
1+ m |
|
||||||
Из сопоставления (12) и (31) следует, что с переходом в упругопластическую область распределение деформаций в вершине трещины становится все более
неравномерным, показатель nre приближается к |
1/r1 |
при m →0 , а распределение |
напряжений выравнивается, т. к показатель nrσ |
приближается 1/r0=1. (рис. 13). |
|
Рис. 13. Распределение напряжений и деформаций в вершине трещины в упругопластической области.
15

3.КРИТЕРИИ РАЗРУШЕНИЯ
При наличии в телах трещин, как в случае однородного, так и в случае неоднородного состояния, используются три группы критериев разрушения: силовые, деформационные, энергетические. При этом возникающие разрушения в зависимости от свойств материала и условий нагружения делятся на три основные группы: хрупкие, квазихрупкие, вязкие.
Рассмотрим пластину с центральной трещиной при действии на нее нагрузки Р (рис. 14). Как известно, в области вершины трещины наблюдается ряд особенностей. Одной из них является наличие зоны пластичности, которая при увеличении нагрузки Р продвигается на величину l как единое целое с вершиной трещины, при этом происходит изменение ее формы и размеров.
Рис. 14. Схема деформирования пластины с трещиной: L -общая деформация;
rT-размер пластической зоны;
δ -раскрытие в вершине трещины; l -приращение длины трещины;
emax-максимальная деформация в вершине трещины;
Зависимость этих параметров от внешней нагрузки Р называется диаграммой разрушения по аналогии с диаграммой деформирования (рис. 15).
Рис.15. Диаграмма разрушения
16
3.1. Характерные признаки видов разрушения
Окончательное разрушение в зависимости от свойств материала и условий нагружения (температура, скорость нагружения), может произойти в любой из точек на кривой ОАВС.
ОА - участок хрупких разрушений. Номинальные напряжения ниже предела текучести, зона пластического деформирования локализована rT<<l . Трещина развивается с высокой скоростью (1200-1500 м/сек). Разрушение описывается критериями линейной механики разрушения (ЛМР). Поверхность разрушения кристаллическая (вязкая составляющая отсутствует Fв=0). Трещина не останавливается.
АВ - квазихрупкое разрушение.
σ ≥ 0,9σT ;rT ~ l. Fв 0 ÷(50 ÷60)%
V 800 ÷1500м/ сек.
Трещина не останавливается. Пластические деформации могут возникать по всему опасному сечению. Для расчетов используются уравнения нелинейной механики разрушения.
ВС - вязкое разрушение.
σ >σT ;rT B;
Fв > 50 ÷60%;V 0 ÷600м/ сек и зависит от скорости нагружения.
Пластические деформации возникают по всему объему тела. Трещина останавливается, если прекратить нагружение (на участках ОА и АВ - не останавливается). Вязкое разрушение описывается нелинейной механикой разрушения.
Таким образом, в области хрупкого разрушения с успехом можно использовать соотношения линейной механики разрушения (ЛМР); в области АВ можно пользоваться ЛМР с рядом допущений; в области ВС методы ЛМР вообще теряют смысл.
В настоящее время 90% всех расчетов на прочность производят для упругой области ОА, этот участок в первую очередь интересует конструктора. В некоторых случаях производятся расчеты и в области АВ, за пределом текучести.
В крайних случаях при расчете по предельному состоянию нагружения можно рассматривать и участок ВС.
Для тел с трещинами (как и без них) используются силовые, деформационные и энергетические критерии разрушения
3.2.Силовые критерии разрушения
3.2.1.Критический коэффициент интенсивности
Очевидно, что идеально хрупкие тела являются идеально упругими, для идеально упругих тел напряженное и деформированное состояние в вершине трещины определяется единственным параметром - коэффициентом интенсивности напряжений (KI
для модели I при условии, что напряжения σ действуют перпендикулярно поверхности трещины).
Если испытывать пластины с различной длиной трещины l, то разрушение будет происходить при достижении нагрузкой критического значения РC (рис. 16).
17

Рис. 16. Диаграмма разрушения хрупкого материала
С увеличением длина трещины при той же ширине пластины 2В разрушающая нагрузка уменьшается, следовательно, уменьшаются и номинальные напряжения по брутто сечению
σC = |
PC |
. |
(32) |
|
|||
|
2BS |
|
|
По результатам испытаний серии образцов с различными длинами исходных трещин строится кривая σC −l . (рис. 17)
Рис. 17. Зависимость разрушающих напряжений от длины трещины (диаграмма разрушения)
Величина σC является силовым критерием, однако малостабильным, т.к. зависит
от размеров пластины 2В, размеров и ориентации трещины, а также от способа нагружения.
Для бесконечного числа форм образцов и длин трещин получается бесконечное множество кривых σC −l и в общей постановке эксперимент теряет смысл. Если же для
данной серии испытаний воспользоваться зависимостью (5) и вычислить |
KI =σ πl fIK |
(33), то при σ =σC величина KI достигнет критического значения KIC и для разрушений |
|
по ОА (рис. 15) при разных σC имеем: |
|
KIC = const |
(34) |
18

В соответствии с предложением Ирвина выражения (33) и (34) позволяют считать КIC инвариантным силовым критерием разрушения, а саму характеристику KIC отнести
к фундаментальным характеристикам материала.
Экспериментальное определение KIC является одним из основных вопросов
механики разрушения и подлежит стандартизации так же, как определение основных характеристик механических свойств материала.
На основе выражения (34) достаточно проводить испытания только одного
образца с трещиной и получить критическое значение КИН |
KIC . Для этого измеряется |
длина трещины, разрушающая нагрузка РC, вычисляется σC |
по (32) и рассчитывается |
KI =σC πl fIK = KIC |
(35) |
Это уравнение является основным при экспериментальном определении KIC.
Для всех других длин трещин разрушающие напряжения можно вычислить, используя выражение (35).
σC = |
KIC . |
(36) |
|
πl fIK |
|
Вместе с тем для большинства конструкционных металлов создание условий хрупкого разрушения по модели I при rT<<l является непростым и в ряде случаев не вытекает из требований практики.
Например, условия хрупкого разрушения (rT<<l) могут быть созданы уменьшением размера зоны пластичности rT путем понижения температуры испытаний
до крайне низких значений, вплоть до Т0K=0, однако очевидно, что практической необходимости в этом случае нет.
С другой стороны, получение условия rT<<l можно добиться увеличением l , но тогда мы окажемся в диапазонах больших длин трещин, которые уже нас не будут интересовать.
В том случае, когда σK <<σT , но размеры зон пластических деформаций при
разрушении достаточно велики, (34) и (35) не выполняются. В этом случае по предложению Ирвина в рассмотрение вводится не фактическая начальная длина трещины l, а условная lT=l+rT, где
rT = |
1 |
|
σ |
|
2 |
|
|
C |
l. |
||
|
2 |
|
σT |
|
|
Тогда
σC′ |
= |
KIC |
. |
(37) |
||
πlT fIK |
||||||
|
|
|
|
|||
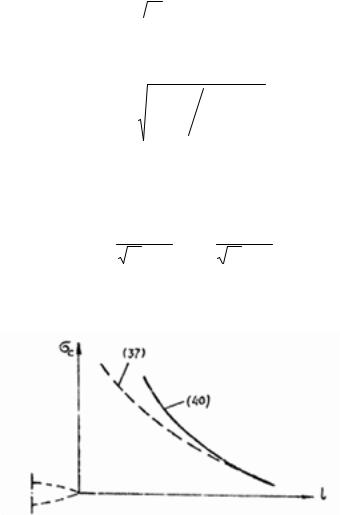
Т.к. lT > l ,то при KIC |
−const следует, что σe′ <σC . |
|
||||
Уравнение (35) используется |
при |
условии 0 ≤σC ≤ 0,6σT , |
а (37) - при условии |
|||
0,6σT ≤σC ≤ (0,9 ÷1,0)σT . |
|
|
|
|
|
|
По мере приближения σT |
|
к σC |
размер rT растет и в зоне разрушения образуется |
|||
макроскопическая деформация, а само разрушение может подчиняться модели I не по
19
всей поверхности излома (рис. 15). На краях поверхность разрушения имеет так называемые «губы среза». Такое разрушение соответствует моделям II и III и в этом смысле разрушение в целом становится смешанным.
Для таких разрушений размер «губ среза» lT составляет до 0,1 толщины и
индекс I для критического значения коэффициента интенсивности напряжений не пишется, т.к.
KC =σC  πl fIK ,
πl fIK ,
или с поправкой на пластическую зону:
KC =σC πl 1+1
|
σ |
2 |
|
|
|
|
|
|
C |
|
f |
|
. |
2 |
σ |
|
IK |
|||
|
|
|
|
|||
|
|
T |
|
|
|
|
(38)
(39)
Если в опыте определить KIC |
или |
КC, то по уравнениям (35) или (38) можно найти |
||
критические напряжения |
|
|
|
|
σC = |
KIC |
,σC = |
KC . |
(40) |
|
πl fIK |
πl fIK |
|
|
Уменьшая размер трещины l в соответствии с выражением (40), линейная |
||||
механика разрушения дает все возрастающие величины σC |
(рис. 18). |
|||
Рис. 18. Зависимость критических напряжении от длины трещины
3.2.2. Предел трещиностойкости
При l →0 получаем σC → ∞ . Таким образом, прочность бездефектных тел
получается бесконечной, однако, это не согласуется с опытами для хрупких тел, для которых при l →0 σC →σв . Если принять какой-либо закон, описывающий реальную
кривую, следует иметь в виду, что характер кривой может быть различен. Для определения формы реальной кривой требуется постановка соответствующих экспериментов.
Проводя опыты при малых длинах трещин устанавливают величины σC . После этого научные результаты аппроксимируют различными способами.
20
