Образец контрольной по курсу «Математика»
Задание №1.
Исследовать
функцию с помощью производной и построить
её график:
Решение.
Область определения функции:
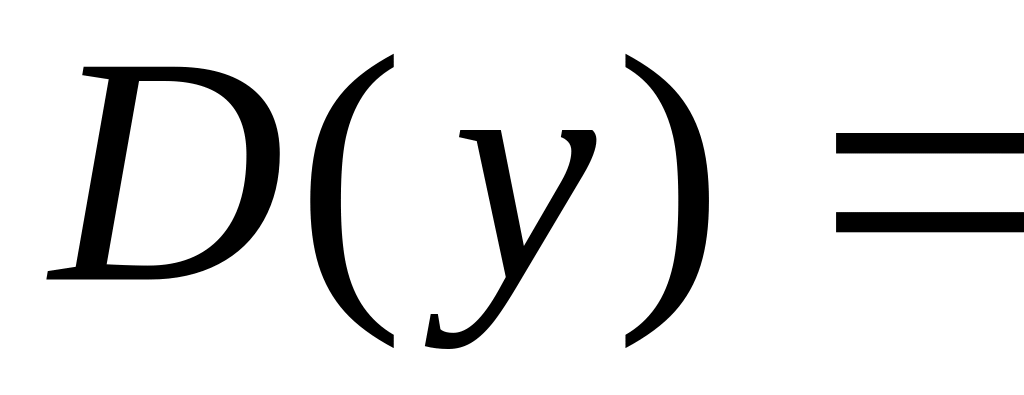
Функция ни четная, ни нечетная; непериодическая.
Нули функции и интервалы знакопостоянства.
– +
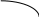
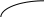
при
;
при
;
.
Интервалы возрастания и убывания функции. Точки экстремумов.
.
– +
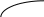
min
убывает
при
и возрастает при
;
.
Интервалы выпуклости и вогнутости графика функции. Точки перегиба.
.
Исследуем знак второй производной.
+
График
функции является выпуклым при
и вогнутым при
Точка
является
точкой перегиба.
.
Асимптоты графика функции.
Так
как
,
то
прямая
является горизонтальной асимптотой
графика функции при
.
Вертикальных асимптот нет.
Используя результаты исследования, построим график функции.
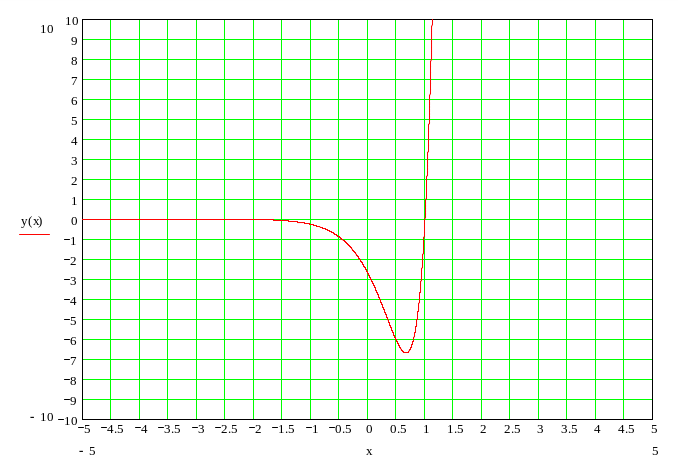
Задание №2.
Задача 1. На кафедре «Высшая математика» преподают 20 человек. Из них профессоров 1, доцентов 6, старших преподавателей 4. Найти вероятность того, что выбранный наугад преподаватель окажется: старшим преподавателем; профессором или доцентом; просто преподавателем; не доцентом или не старшим преподавателем.
Решение.
а)
Обозначим событие
(выбранный
наугад преподаватель окажется старшим
преподавателем). Так как на кафедре
преподают 20 человек, то всего в данном
опыте
исходов. На кафедре 4 старших преподавателя,
поэтому событию
благоприятствует
исхода. Тогда по формуле классической
вероятности находим вероятность события
.
б)
Обозначим событие
(выбранный
наугад преподаватель окажется профессором
или доцентом). На кафедре 1 профессор и
6 доцентов, поэтому событию
благоприятствует
исходов. Тогда по формуле классической
вероятности находим вероятность события
.
в)
Обозначим событие
(выбранный
наугад преподаватель окажется просто
преподавателем). На кафедре работают
преподавателей, поэтому событию
благоприятствует
исходов. Тогда по формуле классической
вероятности находим вероятность события
.
г)
Обозначим событие
(выбранный
наугад преподаватель окажется не
доцентом или не старшим преподавателем).
Событие
наступает только тогда, когда будет
выбран профессор или преподаватель,
поэтому событию
благоприятствует
исходов. Тогда по формуле классической
вероятности находим вероятность события
.
Ответ: а) 0,2; б) 0,35; в) 0,45; г) 0,5.
Задача 2. Бросают 2 игральные кости. Найти вероятность выпадения шестерки хотя бы на одной из них; не выпадения шестерки ни на одной.
Решение. Обозначим события
(шестёрка
выпадет хотя бы на одной из двух костей);
(шестёрка
не выпадет ни на одной из двух костей);
на
i-й
кости шестёрка не выпадет);
.
По формуле классической вероятности находим вероятности
.
Тогда
.
Используя теорему умножения вероятностей
независимых событий, получаем
.
По свойству вероятностей противоположных событий имеем
Ответ:
;
.
Задача 3. Три спортсмена участвуют в сборных соревнованиях. Вероятность зачисления в сборную команду первого, второго и третьего соответственно равны 0,8; 0,7; 0,6. Найти вероятность того, что: хотя бы один из них попадет в сборную; только первый попадет в сборную.
Решение. Обозначим события
(i-й
спортсмен попадёт в сборную);
соответственно
противоположные им события.
По условию задачи известны вероятности
.
По свойству вероятностей противоположных событий находим вероятности
.
а)
Пусть событие
(хотя
бы один из спортсменов попадёт в сборную).
И противоположное ему событие
(ни
один спортсмен не попадёт в сборную).
Тогда
Используя теорему умножения вероятностей независимых событий, получаем
.
По свойству вероятностей противоположных событий имеем
.
б)
Пусть событие
(только
первый спортсмен попадёт в сборную).
Тогда
Используя теорему умножения вероятностей независимых событий, получаем
.
Ответ:
а)
;
б)
.
Задача 4. В коробке находятся т деталей, n из которых стандартные. Наугад извлекаются 2 детали. Найти вероятность того, что: обе детали окажутся стандартными; хотя бы одна стандартная.
Решение. Обозначим события
(i-я
выбранная деталь окажется стандартной);
(i-я
выбранная деталь окажется нестандартной);
а) Пусть событие (обе детали окажутся стандартными);
Событие
равно
произведению событий
.
Используя теорему умножения вероятностей для зависимых событий и формулу классической вероятности, получаем
б)
Пусть событие
(хотя
бы одна из двух деталей будет стандартной).
И противоположное ему событие
(обе
детали будут нестандартными). Тогда
имеем
Используя теорему умножения вероятностей для зависимых событий и формулу классической вероятности, получаем
По свойству вероятностей противоположных событий имеем
Ответ:
а)
;
б)
Задача 5. Четыре студента сдают экзамен. Вероятность сдать экзамен у первого равна 0,85; у второго 0,92; у третьего 0,78; у четвертого 0,65. Найти вероятность того, что только один из них сдаст экзамен; хотя бы один сдаст экзамен; только четвертый сдаст экзамен.
Решение. Обозначим события
(i-й
студент сдаст экзамен);
соответственно противоположные им события.
По условию задачи известны вероятности
.
По свойству вероятностей противоположных событий находим вероятности
.
а) Пусть событие (только один из студентов сдаст экзамен). Тогда
Используя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получаем
.
б)
Пусть событие
(хотя
бы один из студентов сдаст экзамен). И
противоположное ему событие
(ни
один студент не сдаст экзамен). Тогда
Используя теорему умножения вероятностей независимых событий, получаем
.
По свойству вероятностей противоположных событий имеем
.
в) Пусть событие (только четвёртый студент сдаст экзамен). Тогда
Используя теорему умножения вероятностей независимых событий, получаем
.
Ответ:
а)
;
б)
;
в)
.
Задача 6. В коробке находятся две неотличимые по внешнему виду и по весу игральные кости: одна правильная, с одинаковыми вероятностями выпадения всех шести цифр при случайном подбрасывании, другая неправильная, с неравномерным распределением массы по объему. При случайном подбрасывании неправильной игральной кости шестерка выпадает с вероятностью m, единица — с вероятностью n, остальные цифры выпадают с одинаковой вероятностью. Наудачу извлекают игральная кость и подбрасывают. а) Определить вероятность выпадения шестерки. б) Выпала шестерка. Определить вероятность того, что была подброшена правильная игральная кость.
Решение. Обозначим гипотезы
(будет
выбрана правильная игральная кость);
(будет
выбрана неправильная игральная кость);
Пусть событие (при подбрасывании выбранной игральной кости выпадет шестёрка).