Решение. По формуле (2.3.2) имеем разложение рациональной дроби с помощью неопределенных коэффициентов а и в на простейшие дроби:
.
Откуда с учетом
замечания 2.3.1 имеем
.
следовательно
Значит разложение
данной рациональной дроби таково
тогда
.
Пример 2.3.10. Найти
.
Решение. По
формуле (2.3.2) имеем разложение рациональной
дроби
с помощью неопределенных
коэффициентов А ,
и
на простейшие дроби:
.
Откуда с учетом
замечания 2.3.1 имеем
.
следовательно
Тогда
.
2 вид
Замечание
2.3.2. Если многочлен
имеет комплексные корни:
,
кратности k, то в
разложение (2.3.2.) войдут простейшие дроби
вида:
Пример 2.3.11.
Вычислить
.
Решение.
Поскольку корни знаменателя
рациональной дроби в данном интеграле
комплексные
,
с учетом замечания 2.3.2 по формуле (2.3.2)
имеем разложение рациональной дроби
с помощью неопределенных
коэффициентов А,
и
на простейшие дроби:
,
Откуда с учетом
замечания 2.3.1 имеем
.
следовательно
Тогда
.
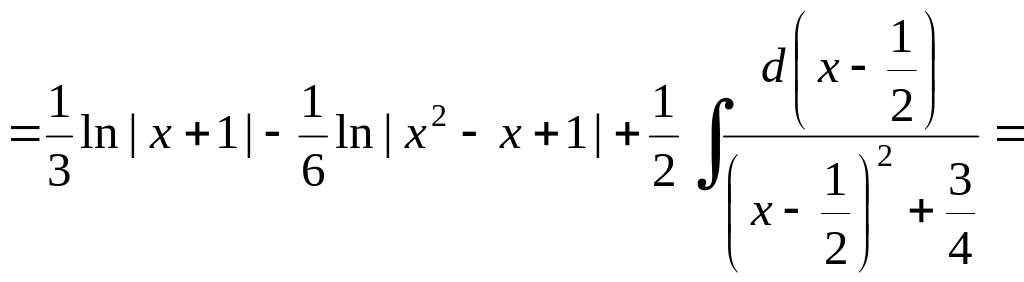
Пример 2.3.12.
Найти
.
Решение.
Подынтегральная функция является
неправильной рациональной дробью:
.
Выделим целую часть, разделив числитель на знаменатель по правилу деления многочленов:
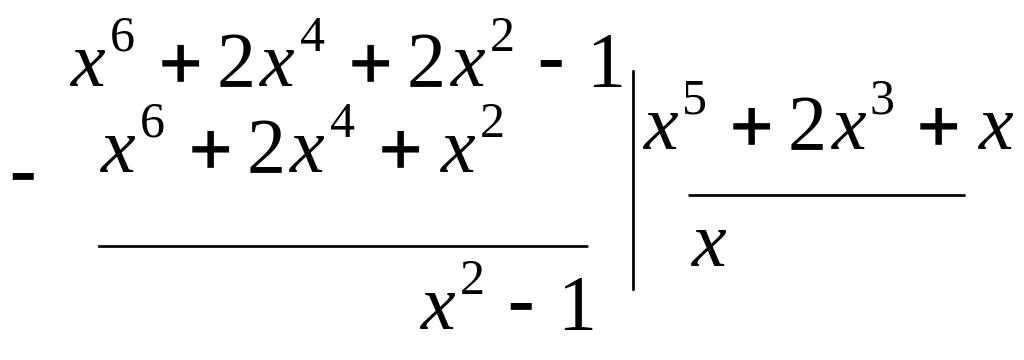
Т.о. подынтегральную
функцию можно представить в виде суммы
целой части и неправильной рациональной
дроби:
,
тогда
.
По формуле (2.3.2)
имеем:
=
.
По замечанию 2.3.1 имеем:
,
следовательно
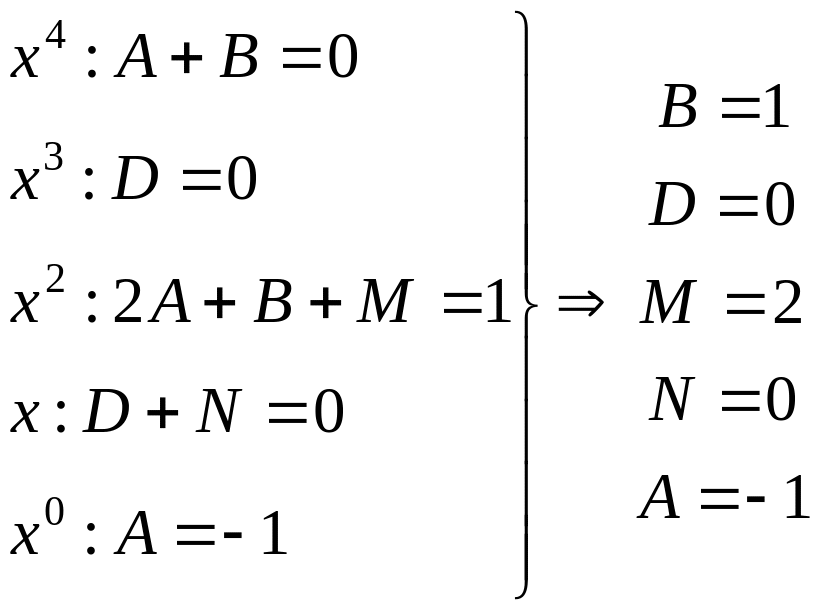
Тогда
=
или окончательно
получим:
.
2.4. Интегрирование тригонометрических функций
1.
Интегралы вида
можно вычислить, если их подынтегральные
функции преобразовать по формулам:
(2.4.1.)
Пример 2.4.1. Найти
.
Решение.
.
Пример 2.4.2. Найти
.
Решение.
.
Пример 2.4.3. Найти
Решение.
.
2. Случай четной степени одной функции.
Рассмотрим интеграл
а)
,
для понижения степени функции
,
используем формулу
б)
,
используем формулу
Пример 2.4.4. Найти
Решение.
.
Пример 2.4.5. Найти
.
Решение.
.
3. Случай нечетной степени одной функции.
а)
- отделением
,
функцию представляем в виде
и производим замену
.
б)
- поступаем аналогичным образом, т.е.
,
затем производим замену
.
Пример 2.4.6. Найти
.
Решение.
.
Пример 2.4.7. Найти
.
Решение.
=
.
4.
Случай произведения двух функций вида:
а) оба показателя
равные, т.е.
,
т.е.
- функцию переписываем в виде
и, применив формулу
,
получим
,
а затем поступаем как в п.2., если
- четное и как в п.3., если
- нечетное.
б) показатели
- четные, но
.
Решение проводим, как в п. 2.(а)
в) если один показатель четен, а другой нечетен, то решаем как в п. 3.
Пример 2.4.8.
Вычислить
.
Решение.
.
Пример 2.4.9. Найти
.
Решение.
.
Пример 2.4.10. Найти
.
Решение.
.
Пример 2.4.11. Найти
.
Решение.
.
5. Случай произведения двух функций вида:
а)
;
б)
(аргументы функций одинаковы).
Для нахождения интеграла используем замену той функции, которая возводится в степень.
Пример 2.4.12. Найти
.
Решение.
Пример 2.4.13. Найти
.
Решение.
.
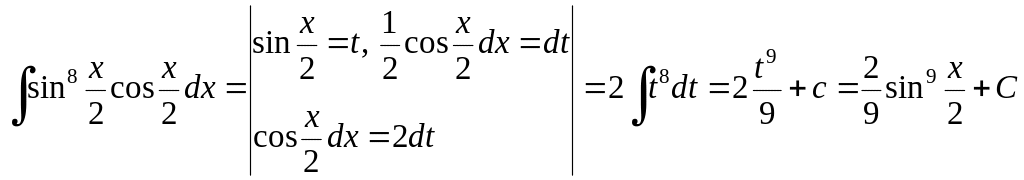6. Случай универсальной тригонометрической подстановки.