2.3. Интегрирование рациональных дробей
Рациональной
дробью (функцией) называется дробь
вида
,
где
и
многочлены.
Рациональная дробь называется правильной, если степень многочлена ниже степени многочлена , в противном случае рациональная дробь называется неправильной.
Если рациональная дробь неправильная, то путем почленного деления числителя на знаменатель по правилу деления многочленов (или с помощью алгебраических преобразований) следует выделить целую часть и неправильную рациональную дробь представить в виде суммы целой части и правильной рациональной дроби.
Поэтому будем рассматривать интегрирование правильных рациональных дробей, поскольку интегрирование целой части не вызывает затруднений.
Простые (правильные) рациональные дроби рассмотрим четырех типов:
,
;
;
,
где
- действие числа; квадратный трехчлен
имеет отрицательный дискриминант,
поэтому на множители не может быть
разложен.
Рассмотрим интегрирование дробей каждого вида.
;
.
Пример 2.3.1. Найти
.
Решение.
.
Пример 2.3.2. Найти
.
Решение.
.
Пример 2.3.3. Найти
.
Решение.
.
Пример 2.3.4. Найти
.
Решение.
=
.
2.3.1. Интегрирование рациональных дробей с помощью выделения полного квадрата
III. При интегрировании рациональных дробей ІІІ типа используем формулы 13, 14, 15 из таблицы основных интегралов, при этом можно выделить такие виды подынтегральных функций:
1. Интегралы вида:
Для того чтобы этот интеграл свети к табличным интегралам, выделим полный квадрат в знаменателе подынтегрального выражения:
где
.
Если
,
то
если
,
то
Интеграл примет
вид:
.
Пример 2.3.5. Найти
.
Решение.
.
Пример 2.3.6. Найти
.
Решение.
.
2. Интегралы вида:
где
Идея вычисления
состоит в том, чтобы из числителя
подынтегрального выражения выделить
производную знаменателя:
,
затем:
.
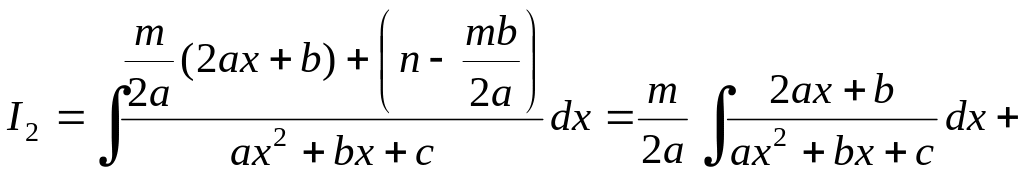
Пример 2.3.7. Найти
.
Решение.
=
.
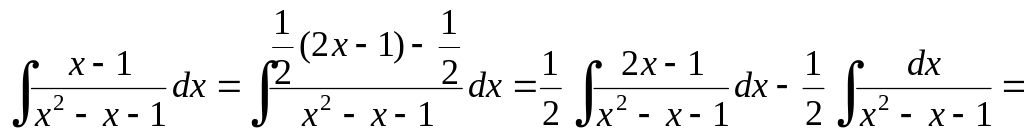
Пример 2.3.8. Найти
.
Решение.
=
.
IV.
Вычисляя интегралы
данного вида, необходимо выделить полный
квадрат в знаменателе, затем, используя
замену переменной, свести к сумме
интегралов вида:
и
.
2.3.2. Интегрирование рациональных дробей с помощью метода неопределенных коэффициентов
Интегрирование рациональной функции после выделения целой части сводится к интегрированию правильной рациональной дроби:
1 вид:
,
где
и
- целые многочлены, причем степень
числителя ниже степени знаменателя.
Если
(2.3.1)
где
- различные действительные корни
многочлена;
- натуральные числа (кратности корней),
то справедливо разложение рациональной
дроби
с помощью неопределенных
коэффициентов
на простейшие дроби:
(2.3.2)
Замечание
2.3.1. Для вычисления неопределенных
коэффициентов
обе части тождества (2.3.2) приводят к
общему знаменателю, а затем, поскольку
получают равные дроби с одинаковыми
знаменателями, а значит и с равными
числителями, то приравнивают числители.
Из курса алгебры известно, что два
многочлена равны тогда и только тогда,
когда равны коэффициенты при одинаковых
степенях переменной х, поэтому их
следует приравнять.
Пример 2.3.9. Найти
.