3. Умова сусідства

Умова сусідства полягає в тому, що сусідні сателіти не повинні зачіплятися один з одним. Якщо k =2, то сателіти розташовуються симетрично один по відношенню до одного - з протилежних сторін по відношенню до центру обертання водила і тому не можуть стикатися один з одним. Таким чином, перевірка на умову сусідства при k =2 не потрібна. При k >2 сателіти можуть стикатися один з одним, і щоб уникнути цього, необхідна перевірка на умову сусідства. Якщо сателітом є блок з 2^х коліс, то перевірка виконується по колесу більшого діаметру.

Хай в нашому прикладі (рисунок 7.17) в блоці сателітів 2-3 колесо 2 більше колеса 3. Колесо 2 зачіпляється з колесом 1. Зобразимо другу проекцію цього зачеплення (початкові кола). Якщо ми маємо число сателітів k, то з'єднавши променями вісь обертання центрального колеса О₁, з центром сусідніх сателітів О₂ і О₂', отримаємо центральний кут між двома сусідніми сателітами О₂О₁О₂' рівний (рисунок 7.1).

З'єднаємо центри сателітів прямою лінією О₂О₂' і з осі обертання центрального колеса О₁ опустимо перпендикуляр О₁К на цю лінію. Отримаємо рівні відрізки О₂К=О₂'К.

З прямокутного трикутника О₁КО₂ знаходимо відрізок О₂К

.

Відрізок О₁О₂ є міжосьовою відстанню коліс 1 і 2:

,

Тоді .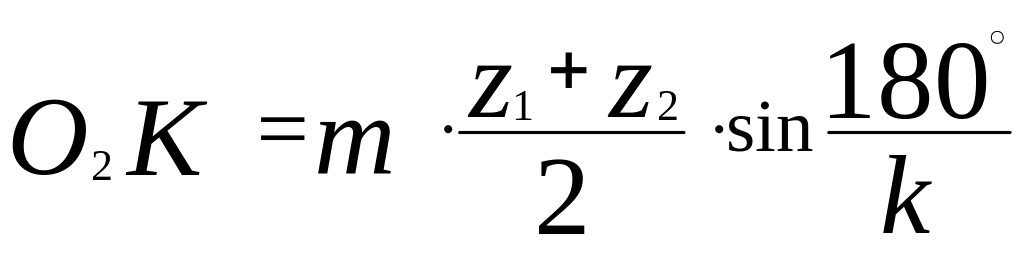

Розглянемо, якою має бути відстань О₂О₂' між центрами сусідніх сателітів, щоб їх зуби не стикалися. З малюнка 3 видно, що ця відстань має бути не менше двох радіусів кіл виступів сателітів - r_a2.Д ля нульових коліс

.

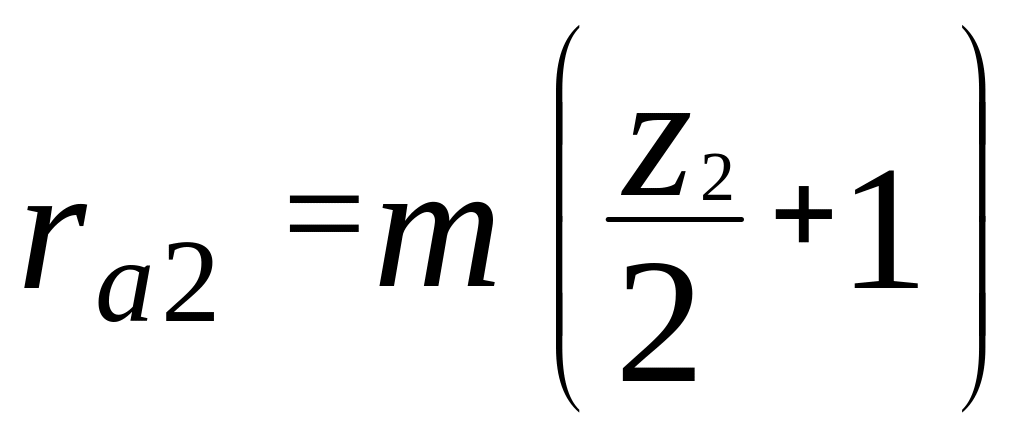Таким чином умову сусідства можна записати у вигляді

.

Підставимо в цю нерівність значення, отримані раніше

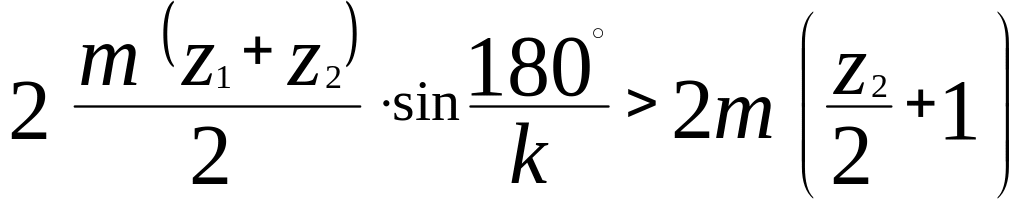
У остаточному вигляді отримаємо

.

Ми отримали умову сусідства для сателітів, які мають зовнішнє зачеплення з центральним колесом. Якби ми розглядали умову сусідства для нашого прикладу сателітів, що мають внутрішнє зачеплення, то з урахуванням того, що міжвісьова відстань в цьому випадку О₁О₂ була б не сумою, а різницею радіусів початкових кіл, то, провівши дослідження аналогічні проведеним вище, отримаємо

.

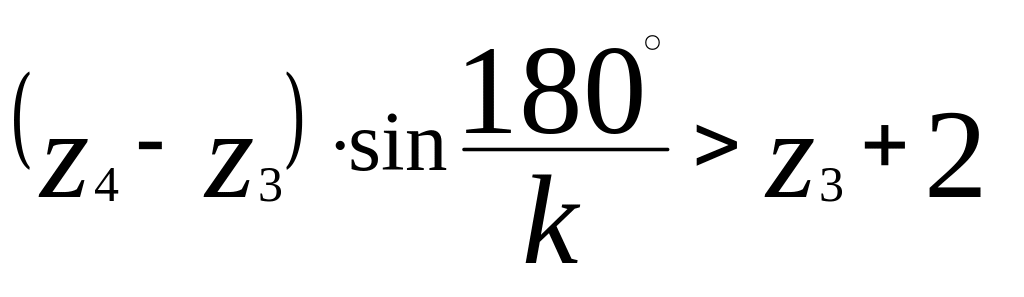IV. Умова складання

Для того, щоб механізм був збалансований, блоки сателітів встановлюють симетрично. При установці сателітів зуби їх не повинні деформуватися і точно збігатися із западинами центральних коліс.

Для виконання умови складання планетарного механізму необхідно враховувати ряд конструктивних особливостей механізму:

1. блоки сателітів встановлюються тільки на рівних відстанях один від одного;

2. всі блоки сателітів геометрично подібні (орієнтація коліс 2, 3 у всіх блоках однакова);

3. сателіти з валом (зубчаті колеса 2 і 3) сполучені жорстко і не провертаються один щодо одного.

Якщо ми хочемо, щоб зуби сателітів точно збігалися із западинами центральних коліс, необхідно витримати певні співвідношення між числами зубів центральних коліс і коліс сателітів - це і буде умовою складання.

Розглянемо умову складання на прикладі планетарного механізму, зображеного на рисунку 7.17. Зобразимо другу проекцію центральних коліс 1 і 4 (рисунок 7.17). Припустимо, що нам необхідно встановити 2 блоки сателітів між колесами 1 і 4. Хай виявилось, що колеса 1, 4 зорієнтовані таким чином, що вгорі зуб колеса 4 встановлений напроти зуба колеса 1, а внизу - зуб колеса 4 проти западини колеса1. Якщо вгорі ми зможемо встановити блок сателітів 2, 3, то внизу це виявиться неможливим. Сателіти геометрично подібні і тому необхідно, щоб орієнтація зубів коліс 1 і 4 була внизу і вгорі однакова.

Перший сателіт можна завжди встановити, зорієнтувавши колеса 1 і 4 так, як це необхідно. Коли перший сателіт встановлений, колеса 1 і 4 взаємно зорієнтовані, тобто ми вже не можемо отримати будь-яке взаємне розташування їх зубів, оскільки орієнтація коліс тепер вже залежитиме від сателіта.

Розглянемо, коли ми зможемо встановити 2^й сателіт на місце 1^го. Якщо не враховувати умову сусідства, то теоретично наступний сателіт ми можемо встановити повернувши колесо 1 на один крок, тобто на кут

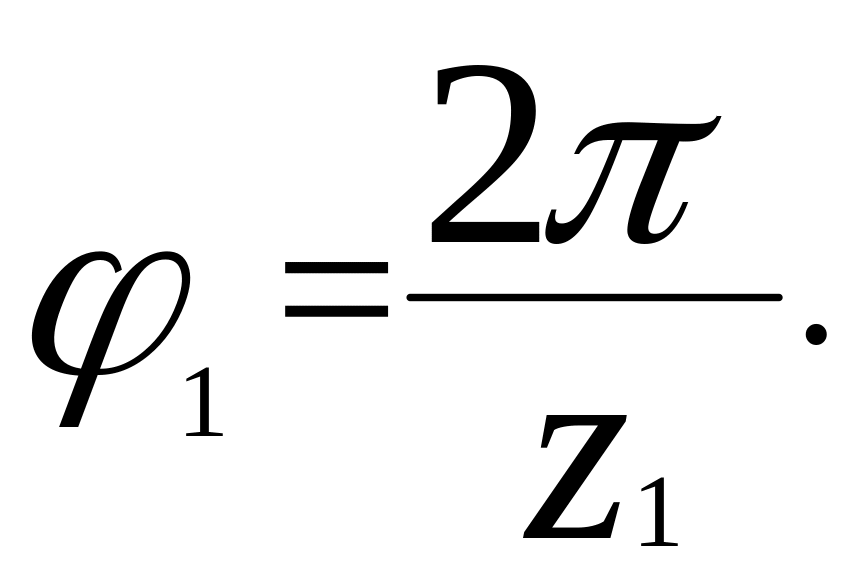
При повороті колеса 1 на кут ₁ обернеться і водило Н, оскільки перший блок сателітів вже встановлений. Визначимо на який кут обернеться водило Н при повороті колеса 1 на кут ₁ , скориставшись передаточним відношенням.

.

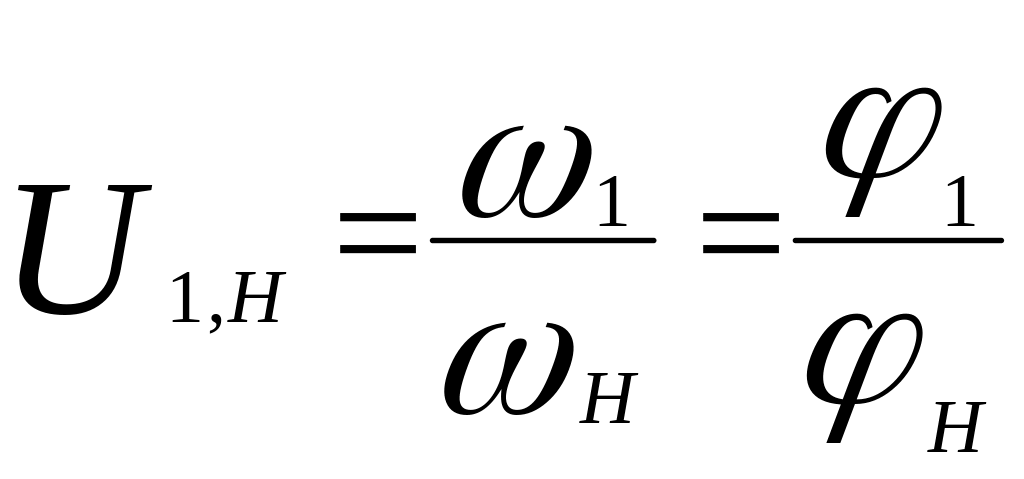
Звідси визначимо кут повороту водила

.

О

сателіт

чевидно, що теоретично ми можемо встановити обмежене число сателітів. Їх кількість буде залежною від кута повороту водила, оскільки водило переносить блок сателітів. Підготувавши для установки наступного сателіта місце, повертаючи колесо 1 на 1 крок, ми тим самим повернули водило на деякий кут _Н. Якщо _Н=2, то на це місце повернеться 1^й сателіт.

Таким чином теоретично можливе число сателітів Е ми можемо визначити, розділивши 2 на кут повороту водила _Н при повороті першого колеса на кут ₁.

.

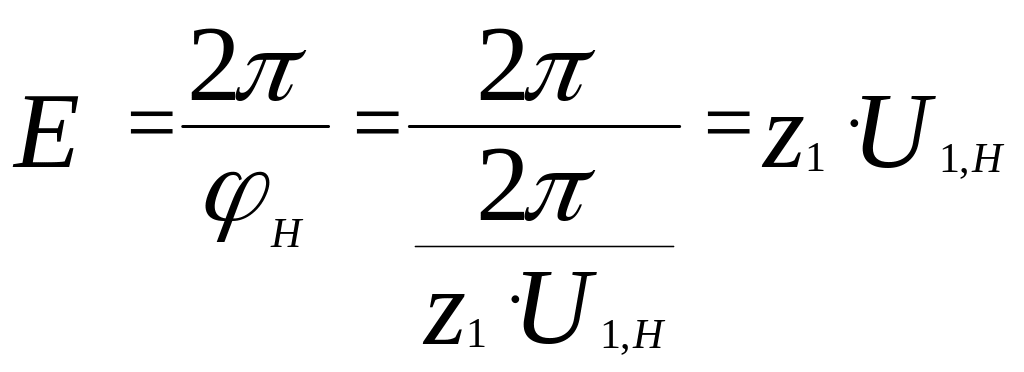Припустимо, що нам необхідно встановити k сателітів - ціле число.

Розділивши теоретично можливе число сателітів Е на необхідне нам число сателітів k, отримаємо деяке число 

,

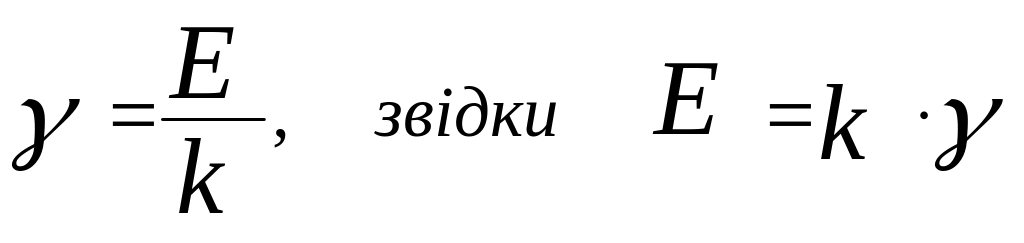Де k - число сателітів - ціле число;

Е - теоретично можливе число сателітів - теж ціле число;

• - будь-яке ціле число.

Підставимо набутого значення Е в попередню формулу

.

Отримаємо умову складання для планетарного механізму в загальному вигляді. Права частина рівняння має бути кратною числу сателітів k.

Визначимо умову складання планетарного механізму, зображеного на рисунку 7.17.

Визначимо передаточне відношення за формулою Вілліса:

,

.

Записуємо умову складання:

.

У остаточному вигляді отримаємо

.

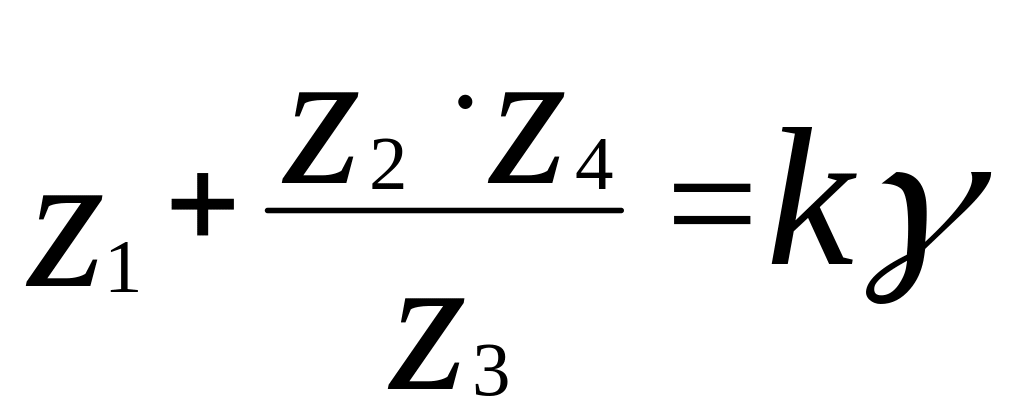Як правило, число сателітів k дорівнює 3. Три сателіти саморозташовуються і контактують з колесами в 3^х точках. Відбувається рівномірний розподіл навантаження між сателітами.

Аналогічно отримуємо

а) б)