
- •1. Предм, метод и задачи ст-ки.
- •2. Совок-ть и стат-ая зак-ть.
- •1. Массовость явлений (з-н больших чисел).
- •2. Качественная однородность
- •4. Программа набл. Объект и ед.А набл.
- •5. Группировка, сводка и сист стат-их пок-лей
- •6. Стат-ий анализ стр-ры
- •7. Стат табл и граф.
- •8. Средние величы
- •9. Понятие вариац, вариационного ряда и их виды
- •10. Графическое изображение вариационных рядов
- •11. Абсолютные показ вариац.
- •12. Относительные показ вариац.
- •13. Выборочное набл.
- •14. Сред и предельная ошибки выборочного набл.
- •15. Определение необходимой численности выборки.
- •16. Малая выборка
- •17. Индексы
- •18. Агрегатные индексы
- •19. Индексы средние из индивидуальных.
- •20. Индексы переменного постоянного состава и структурных сдвигов.
- •21. Факторный индексный анализ.
- •22. Понятие функциональной и статистицеской связи
- •23. Корреляционно-регрессионный анализ (общая хар-ристика).
- •24. Понятие рядов динамики и их виды
- •25. Аналитические показ динамики.
- •26. Средние показ динамики
- •27. Тенденции.
- •29. Показ естественного и механического движения населения.
- •30. Табл смертности.
- •31. Прогноз численности населения
- •32. Основные источники данных по ст-ке занятости:
- •33. Изучение Экон Акт Насел(эан), занятости и безработицы.
- •34. Показ движения рабочей силы.
- •35. Показ использования рабочего времени.
- •37. Денежные агрегаты
- •38. Показ ст-ки денежного обращения.
- •39.Денежный мультипликатор.
- •40. Показ скорости обращ денег.
- •41. Баланс денежных доходов и расходов населения
- •42. Инфляция
- •43.Стат-ие показ инфляции и их анализ.
- •44. Индексы потребительских цен.
- •46. Оценка вариационного ряда на асимметрию и эксцесс
- •47. Структурные средние в вариационных рядах.
- •48. Децили.
- •49. Методы вычисления трендовой компоненты в рядах динамики.
- •50. Факторный анализ уровня инфляции.
- •51. Цепные и базисные индексы
- •52. Половозрастная структура населения
- •54. Основные показ ст-ки цен.
- •1. Предм, метод и задачи ст-ки.
14. Сред и предельная ошибки выборочного набл.
Каждый вид выборки определяется целями исслед, при которых достигается наименьшая ошибка репрезентативности. Расчет стандартных ошибок разработан математической ст-кой и эти ошибки рассчитываются для двух параметров - выборочной средней и выборочной доли.
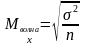
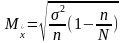
Стандартная ошибка для бесповторного отбора всегда меньше, чем для повторного отбора.
Аналогично для стандартной ошибки доли:
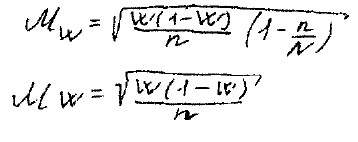
В этих Ф-лах предполагается, что дисперсия относ к ген совок-ти. Как правило, эта велич неизвестна.
Математически доказано, что выборочная дисперсия имеет определённое соотношение с дисперсией ген совок-тью:
![]()
При большом числе наблй n, вся дробь стремиться к 1, поэтому в этих Ф-лах в качестве дисперсии используется выбороч дисперсия.
![]()
Вышеуказанные формулы разработаны для собственного случайного и механического отбора.
Помимо стандартной ошибки репрезентативности необходимо вычислить предельную ошибку выборочной средней и выборочной доли.
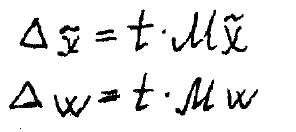
Критерий t - критерий доверия, заданный с определённой вероятностью, согласно интегральной функцией Лапласа.
![]()
На практике при организации выборочного набл возн пробл, что принять в качестве дисперсии. В таких случаях приняты следующие варианты выбора дисперсии:
1. Используя опыт аналогичных наблй, принимают сигму, равную:
![]()
2. Если распределение данных генеральной совок-ти предполагается асимметричным, то сигма будет равна:
![]()
З.Если распределение предполагается умеренно асимметричным (приближение к нормальному распределению), то:
![]()
На подготовительной стадии проведения выборки исследователь задаёт предполагаемые значения доверительной вероятности, стандартные ошибки, и отсюда определяется предполагаемая численность выборки.
![]()
Для бесповторной выборки Ф-ла корректируется на велич Vа генеральной совок-ти.
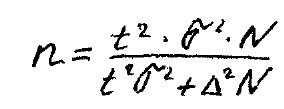
Иногда, вместо значения предельной ошибки выборки задаётся желаемая (предполагаемая) ошибка в виде относительной величы в процентах:
![]()
В таких случаях расчёт Vа выборки имеет другую формулу:
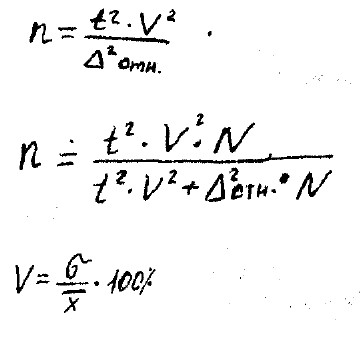
V - коэффициент вариац в процентах.
Как было сказано ранее, выборочное набл может осуществляться по различным схемам. Соответственно, меняется методика расчета стандартных ошибок, что связано с расчётом с дисперсией.

15. Определение необходимой численности выборки.
Обьем выборки определяется след Ф-лами:
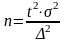 ,
для повторн.
,
для повторн.
Если процентный обьем выборки не превышает 5% от численности ген сов-сти, к след форм-ле можно не переходить, это существенно не скажется на результате
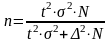 ,
для бесповт.
,
для бесповт.
В
качестве оценок генер дисперсии (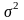 )
можно использовать след соотнош
)
можно использовать след соотнош
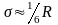 -для
нормального распределения
-для
нормального распределения
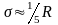 -для
асимметричного распределения.
-для
асимметричного распределения.
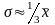
R-размах=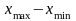
В качестве оценки ген дисперсии доли используют максимально возможную дисперсию альтернативного признака.
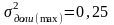
16. Малая выборка
Выборочное набл, которое составляет менее 30 ед., получило назв малой выборки
Необходимость использования малой выборки связана, главным образом, с понятием производственного эксперимента, а так же, зачастую, с невозможностью получить большее число наблй в силу специфики изучаемого явл.
Однако, малая выборка, в отличие от нормальной выборки, связана с особенностями расчета нормальных ошибок и доверительных интервалов.
Дело в том, что при сокращении числа наблй хар-р изучаемых ед. совок-тей резко отличается от нормального распределения Лапласа. Поэтому, английским математиком и ст-ком Госсеном (псевдоним Стьюдент) были разработаны значения t-критерия для нормированных велич, распределение которых при числе наблй от 30-и до 100 приближается к нормальному, а при 100 и более -полностью соответствуют нормальному.
![]()
На основе малой выборки доверительные интервалы можно определить лишь при условии, что генеральная совок-ть имеет нормальное распределение ошибок. Распределение Стьюден-та явл так же симметричным, только более пологим. В этом распределении только один параметр - df -число степеней свободы изучаемого признака.
Для малой выборки это число степеней свободы равно n-1, так как оно представляет то число значений признака, которое необходимо для расчёта средней величы и дисперсии.
![]()
Предельная ошибка равна:
w=t*S
