46. Оценка вариационного ряда на асимметрию и эксцесс
Для хар-ристики формы распределения используются коэффициенты асимметрии и
эксцесс.
Коэффициенты могут быть исчислены в двух вариантах.
1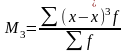
.
Моментный
коэффициент асимметрии.
Данный коэффициент имеет знак "+" при правосторонней асимметрии и "-"при левосторонней. Значение этого коэффициента при асимметрии должно быть оценено на существенность (стат-ую значимость). Для этой цели рассчитывается сред ошибка этого коэффициента, которая зависит от Vа изучаемой совок-ти и рассчитывается по формуле
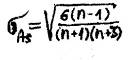
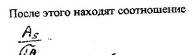
Если оно оольше 3, то асимметрия считается существенной, если меньше - не существенной.
Основным недостатком момент-ного коэффициента асимметрии явл то, что его велич зависит от количества резко выделяющихся (нетипичных) ед. совок-ти. Если совок-ть содержит такие ед, этот коэффициент малопригоден, поэтому английским стом Карлом Пирсоном был предложен другой вариант расчета этого показателя:
При использовании этого показателя след считаться с наличием умеренной асимметрии. Распределение с умеренной асимметрией должны иметь следующее соотношение:
Эксцесс. То есть, островершинность или плосковершинность распределения.
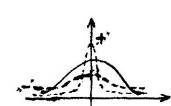
Что бы проверить изучаемое распределение на наличие эксцесса, рассчитывают следующий показ:
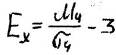
Для нормального распределения это соотношение
соответствует значению, равному 3. "+" - более островершинное, "-" -более пологое.
Иногда при анализе вариац на основе рядов распределения можно столкнуться с распределениями:
Две моды - бимодальное распределение.
-
антимода.
47. Структурные средние в вариационных рядах.
Для хар-ристики структуры изучаемой совок-ти по какому-либо признаку используются различного рода показ:
-Среднее значение (центр распределения) -Мода -Медиана
-Квантили различного рода (квинтили, децили, персентели)
Мода - значение признака, который наиболее часто встречается в изучаемой совок-ти. Если ряд дискретный, то это значение соответствует наибольшей частоте.
Для
интервального ряда есть такая Ф-ла
расчёта:
Обозначения:
хо - нижняя граница модального интервала
i - велич интервала Fm0 - частота модального интервала
Fm0-1- частота предмодального интервала
Fm0+1 – частота послемодального интервала
Медиана - значение признака, которое делит совок-ть на две равные части. Для того, что бы рассчитать дискретный ряд, нужно:
X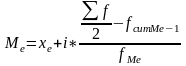
e-нижняя
граница медианного интервала
FcumMe-1- накопленные частоты предмедианного интервала
FcumMe- накопленные частоты медианного интервала
Медианным интервалом считается тот, в котором сумма накопленных частот составляет >50%
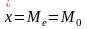
Такое соотношение между средними говорит, что распределение имеет правостороннюю асимметрию, то есть большая часть выше среднего уровня.
Правостороннее
Симметричное
Рассмотренные показ часто используют на практике, Например, средние цены на потребительском рынке, мировые цены - модальные цены.
В дополнение к рассмотренным показателям (мода, медиана) при изучении вариац применяются и другие показ её хар-ристики.
R=Xmax-Xmin – размах вариации, разница между макс и мин значениями.
С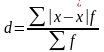
реднее
линейное отклонение, мера колеблимости
вокруг средней величины
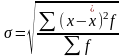
СКО-средне квадратическое отклонение
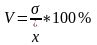
Коэффициент вариации, характеристика однородности (неоднородности) изучаемой совокупности.