Свойства нормального распределения.

• Нормальное распределение есть распределение вероятности суммы независимых случайных величин с конечными дисперсиями при неограниченном увеличении числа слагаемых.

С точки зрения процесса измерений нормальное распределение погрешностей есть результат одновременном действия большого числа независимых факторов, каждый из которых незначительно и независимо от других оказывает в влияние на суммарную погрешность измерений. Именно по этому случайная погрешность измерений наиболее часто описываются законом нормального распределения поскольку

В реальности мы всегда имеем дело с ограниченным числом источников погрешностей. Однако, при сложении даже только четырех-пяти случайных величин с различными законами распределения, но с соизмеримыми дисперсиями (т.е. со сравнимыми величинами погрешностей), мы приходим к закону распределения погрешностей, близкому к нормальному. Особенно, если плотность вероятности достаточно велика

Ф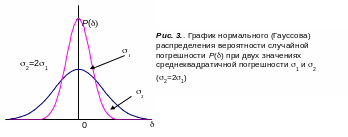 ункция распределения вероятности p() определяет вероятность того, что величина случайной погрешности окажется равной заданной. Нормальное распределение плотности вероятности p() центрированной случайной погрешности  описывается функцией Гаусса:

…10

где:  - величина случайной погрешности,  - среднеквадратическое отклонение измеряемой величины от истинной.

Из (10) следует:

1). Площадь, ограниченная графиком и осью абсцисс, всегда остается неизменной и равной 1 при любых значениях , что соответствует тому, что вероятность появления ошибки, отличной от нуля равна р(0)=1:

…11

2). Вероятность того, что величина случайной погрешности окажется в интервале от =- до =+а, определяется соотношением:

…12

Если выразить величину интервала в единицах , т.е. принять  = t, где t – безразмерный коэффициент, и таким образом связать величину ожидаемой погрешности = со среднеквадратичным отклоне­нием, то интеграл (12) можно преобразовать к виду, который определяет вероятность нахождения величины погрешности в интервале =t и называется интегралом ошибок:

(13)

Значения интеграла ошибок Ф(t) заранее вычислены, затабулированы и широко используются в практических расчетах. С его помощью при нормальном законе распределения можно вычислить вероятность того, что величина случайной погрешности лежит в некотором заданном интервале значений.

В частности:

• P(-3<3)=2Ф(3)=0,9972 - случайная составляющая погрешности измерения с вероятностью 0,9972 не выходит за пределы интервала 3

• P(-2,67<<2,6)=2Ф(2,6)=0,99 - случайная составляющая погрешности измерения с вероят­ностью 0,99 лежит в пределах 2,6

• P(-2<<2)=2Ф(2)=0,95 - случайная составляющая погрешности измерения с вероят­ностью 0,95 лежит в пределах интервала 2.

• Р(-(-<<)=2Ф(1)=0,68 - вероятность того, что величина погрешности не превышает своего среднеквадратического значения составляет 0,68

Когда число отдельных изме­рений достаточно велико, N  30, то с высокой степенью точности можно считать среднеарифметическое значение измеряемой величины равным среднему, принимаемому за ее действительное значение. При этом среднеквадратическое отклонение отдельного измерения ₀ равно среднеквадратическому отклонению многократного измерения _А и соответствующему параметру закона нормального распределения .

;