Теория вероятности. Билеты и ответы

vk.com/club152685050 | vk.com/id446425943

1. Понятие события. Виды и взаимосвязь событий.

Теория вероятностей — математическая наука, изучающая закономерности массовых случайных явлений (событий).

Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом).

Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, to выпадение пятерки — событие.

События будем обозначать заглавными буквами латинского алфавита: A, В, С, ... .

Пусть при n испытаниях событие A появилось m раз.

Отношение m/n называется частотой (относительной частотой) события A и обозначается Р*(А)=m/n

Опыт показывает, что при многократном повторении испытаний частота Р*(А) случайного события обладает устойчивостью. Поясним это на примере.

Пусть при бросании монеты 4040 раз герб выпал 2048 раз. Частота появления герба в данной серии опытов равна Р*(А)=m/n=2048/4040=0,5069. При бросании той же монеты12000 раз герб выпал 6019 раз. Следовательно, в этом случае частота Р*(А)=6019/12000=0,5016. Наконец, при 24000 бросаний герб появился 12012 раз с частотой Р*(А)=0,5005. Таким образом, мы видим, что при большом числе бросаний монеты частота появления герба обладает устойчивостью, т. е. мало отличается от числа 0,5. Как показывает опыт, это отклонение частоты от числа 0,5 уменьшается с увеличением числа испытаний. Наблюдаемое в этом примере свойство устойчивости частоты является общим свойством массовых случайных событий, а именно, всегда существует такое число, к которому приближается частота появления данного события, мало отличаясь от него при большом числе испытаний. Это число называется вероятностью события. Оно выражает объективную возможность появления события. Чем больше вероятность события, тем более возможным оказывается его появление. Вероятность события A будем обозначать через Р(А). В рассмотренном выше примере вероятность появления герба, очевидно, равна 0,5.

Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти.

Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара

— достоверное событие; появление белого шара — невозможное событие.

Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.

Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1) — вероятности события A.

vk.com/club152685050 | vk.com/id446425943

Совмещением (или произведением) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА.

Аналогично, совмещением нескольких событий, например A, В и С, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С.

Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В.

Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С.

Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное.

vk.com/club152685050 | vk.com/id446425943

2. Классическая, статистическая и геометрическая вероятность.

Классическая вероятность:

Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:

Это определение вероятности часто называют классическим. Можно показать, что классическое определение удовлетворяет аксиомам вероятности.

Пример: На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность P(A) того, что взятый наудачу подшипник окажется стандартным.

Решение: Число стандартных подшипников равно 1000—30=970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит

из N=1000 равновероятных исходов, из которых событию A благоприятствуют М=970 исходов. Поэтому P(A)=M/N=970/1000=0.97

Статистическая вероятность:

Классическое определение не требует проведения опыта. В то время как реальные прикладные задачи имеют бесконечное число исходов, и классическое определение в этом случае не может дать ответа. Поэтому в таких задачах будем использовать статическое определение вероятностей, которое подсчитывают после проведения эксперимента или опыта.

Статической вероятностью w(A) или относительной частотой называют отношение числа благоприятных данному событию исходов к общему числу фактически проведенных испытаний.

w(A)=nm Относительная частота события обладает свойством устойчивости:

limn→∞P( nm−p <ε)=1 (свойство устойчивости относительной частоты)

Геометрическая вероятность:

Определение геометрической вероятности используется в задачах, когда общее и благоприятное число исходов бесконечно.

Бросается наудачу точка в область G. Найти вероятность того, что точка попадет в область g (множество g с квадрируемой границей).

Вероятность в этом случае будет вычисляться по формуле

p=mes(g)mes(G)

x, y находится в [0;60] (определение того, что встреча произойдет между 12 и 13 часами, то есть в промежуток времени в 60 минут) - задает область G.

vk.com/club152685050 | vk.com/id446425943

Пример: Два студента условились встретиться в определенном месте между 12-ю и 13-ю часами. Пришедший первым ждет другого не больше 20 минут, после чего уходит. Найти вероятность того, что встреча произойдет.

Решение:

Пусть x - момент времени прихода первого студента

Пусть y - момент времени прихода второго студента

x, y находится в промежутке [0;60] (определение того, что встреча произойдет между 12 и 13 часами, то есть в промежуток времени в 60 минут) - задает область G.

|x-y| ≤20 (определение того, что студент пришедший первым ждет второго не больше 20 минут) - задает область g.

Тогда области, задаваемые неравенствами, будут выглядеть следующим образом.

Тогда вероятность будет считаться как отношение площадей двух областей g и G. p(A)=60*6060*60−40*40=94

vk.com/club152685050 | vk.com/id446425943

3. Теорема сложения вероятностей (вывод).

Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий.

Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В – попадание при втором выстреле, то событие А+В – попадание хотя бы при одном выстреле (или при первом выстреле, или при втором, или в обоих случаях).

Теорема 1.(теорема сложения вероятностей):

Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

P(A+B)=P(A)+P(B) (3)

Доказательство: Введем обозначения: n – общее число возможных элементарных исходов испытания; m1 – число исходов, благоприятствующих событию А; m2 – число исходов, благоприятствующих событию В.Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно

m1+m2. Следовательно, P(A+B)=(m1+m2)/n=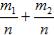. Приняв во внимание, что m1/n=P(A) и m2/n=P(B), окончательно получим P(A+B)=P(A)+P(B)

Следствие 1. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

P(A1+A2+...+An)=P(A1)+P(A2)+...+P(An)

Пример 3. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.

Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного шара (событие А) P(A)=10/30=1/3 Вероятность появления синего шара (событие В) P(B)=5/30=1/6 События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета),

поэтому теорема сложения применима. Искомая вероятность P(A+B)=P(A)+P(B)=

Теорема 2. Сумма вероятностей событий А1, А2, …, Аn, образующих полную группу, равна единице:

P(A1)+P(A2)+...+P(An)=1 (4)

Доказательство: Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то:

P(A1+A2+...+An)=1 (5)

любые два события полной группы несовместны, поэтому можно применить теорему сложения:

P(A1+A2+...+An)=P(A1)+P(A2)+...+P(An) (6)

Сравнивая (4) и (5), получим P(A1+A2+...+An)=1

vk.com/club152685050 | vk.com/id446425943

Два несовместных события, образующие полную группу называются противоположными событиями. Если

Пусть в результате испытания возможны только два единственно возможных события.

Например,

а) при одном бросании монеты - "выпал герб" и "выпала цифра";

б) при одном бросании игральной кости - "выпало 6 очков" и "не выпало 6 очков";

с) при одном выстреле - "попадание в мишень" и "не попадание в мишень".

В каждой паре событий появление одного исключает появление второго. Действительно, если монета выпала гербом, то уже не может выпасть цифрой; игральная кость не может одновременно выпасть сразу двумя гранями; стрелок попадая в мишень, исключает промах. Итак, данных примерах противоположными событиями являются: а) A={выпал герб}, A (-)={выпала цифра}; б) B={выпало 6 очков}, B (-)={не выпало 6 очков}; с) C={попадание в мишень}, C (-)={не попадание в мишень}.

vk.com/club152685050 | vk.com/id446425943

4. Зависимость событий. Теория умножения вероятностей (вывод).

Во многих задачах приходится находить вероятность совмещения событий А и В, если известны вероятности событий А и В.

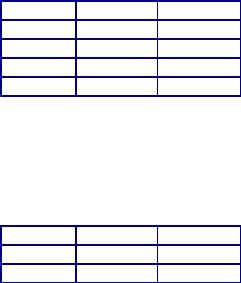
Рассмотрим следующий пример. Пусть брошены две монеты. Найдем вероятность появления двух гербов. Мы имеем 4 равновероятных попарно несовместных исхода, образующих полную группу:

Таким образом, P (герб,герб)=1/4.

Пусть теперь нам стало известно, что на первой монете выпал герб. Как изменится после этого вероятность того, что герб появится на обеих монетах? Так как на первой монете выпал герб, то теперь полная группа состоит из двух равновероятных несовместных исходов:

При этом только один из исходов благоприятствует событию (герб, герб). Поэтому при сделанных предположениях Р(герб,герб)=1/2. Обозначим через А появление двух гербов, а через В — появление герба на первой монете. Мы видим, что вероятность события А изменилась, когда стало известно, что

событие B произошло.

Новую вероятность события А, в предположении, что произошло событие B, будем обозначать PB(А).

Таким образом, Р(A)=1/4; PB(А)=1/2

Теорема умножения.

Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.

P(AB)=P(A)PA(B)

Доказательство. Докажем справедливость соотношения (4), опираясь на классическое определение вероятности. Пусть возможные исходы Е1, Е2, ..., ЕN данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют M исходов, и пусть из этих M исходов L исходов благоприятствуют событию B. Очевидно, что совмещению

событий A и B благоприятствуют L из N возможных результатов испытания. Это дает:

; ;

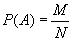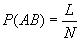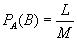
Таким образом,

vk.com/club152685050 | vk.com/id446425943

Поменяв местами A и B, аналогично получим:

Теорема умножения легко обобщается на любое , конечное число событий. Так, например, в случае трех событий A1, A2, A3 имеем:

В общем случае:

vk.com/club152685050 | vk.com/id446425943

5. Независимость по совокупности. Формула полной вероятности (вывод).

Независимость по совокупности:

Р(Аi)P(Aj)=P(AiAj)

P(Ai)P(Aj)P(Ak)=H(AiAjAk)

……………………………….

P(Ai)P(Aj)…….P(An)=P(AiAj…….An)

Если в данном примере выполняются все эти условия, то событие называется независимым по совокупности.

Например, если при проверке этих условий, не выполняется равенство в какой-то паре, то говорится, что событие имеет попарную зависимость.

Формула полной вероятности:

Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,

Применяя аксиому сложения вероятностей, имеем:

Но 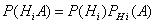(i=1, 2, ..., n), поэтому

Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».

vk.com/club152685050 | vk.com/id446425943

6. Формула Байеса (теорема гипотез) (вывод).

Теорема Байеса, Формула Байеса — одна из основных теорем элементарной теории вероятностей, которая позволяет определить вероятность того, что произошло какое-либо событие (гипотеза) при наличии лишь косвенных тому подтверждений (данных), которые могут быть неточны. Названа в честь ее автора, преп. Томаса Байеса(посвященная ей работа «An Essay towards solving a Problemin the Doctrine of Chances» впервые опубликована в 1763 году,[1] через 2 года после смерти автора). Полученную по формуле вероятность можно далее уточнять, принимая во внимание данные новых наблюдений. Психологические эксперименты показали, что люди при оценках вероятности игнорируют различие априорных вероятностей (ошибка базовой оценки), и потому правильные результаты, получаемые по теореме Байеса, могут очень отличаться от ожидаемых.