Теория вероятности. Билеты и ответы

vk.com/club152685050 | vk.com/id446425943

15. Понятие моментов. Основные свойства.

Моментслучайной величины —числоваяхарактеристика распределенияданнойслучайнойвеличины.

Еслиданаслучайная величина определённая нанекотором вероятностном пространстве, то: -мначальныммоментом случайнойвеличины где называетсявеличина

еслиматематическоеожидание вправойчастиэтогоравенства определено; -мцентральным моментом случайной величины называетсявеличина

-мабсолютными- мцентральным абсолютныммоментамислучайной величины называется соответственно величины

еслиматематическоеожидание вправойчасти этогоравенстваопределено.

Абсолютныемоментымогут бытьопределены нетолькодляцелых k,ноидлялюбыхположительныхдействительных вслучае, еслисоответствующиеинтегралы сходятся.

Основныесвойствамоментовслучайныхвеличин:

1)M[c] =∫ (c) f(x)dx=c∫f(x)dx=c

2)M[cx]=∫cxf(x)dx=c∫xf(x)dx=cMx

3)M[cx+k]= cMx+k

4)M[x1+x2+x3+...+Xn]=∑ Mx1

5)M[x1,x2,x3,...,xn]=∏ Mx1

6)D[c]=∫((c-m(c))^2) f(x)dx=∫((c-c)^2) f(x)dx=0

7)D[cx]= M[((cx-m(cx))^2)]=(c^2) Dx

8)D[x+-y]= Dx+Dy+-2M[x,y]

vk.com/club152685050 | vk.com/id446425943

ïïåi (x i - m X /Y )2 × P{X = x i /Y = y j },СВДТ .

î

Приведенные выше формулы для числовых характеристик двумерного случайного вектора без труда обобщаются на случай n-мерного случайного вектора (Х1, Х2, ..., Хn). Так, например, вектор с неслучайными координатами (m1, m2, ..., mn), где mi - математическое ожидание СВ Хi, определяемое формулой

Ковариационной матрицей n-мерного случайного вектора X = (Х1, Х2, ..., Хn) называется симметрическая матрица, элементы которой представляют собой ковариации соответствующих пар компонент случайного

,

Корреляционной матрицей n-мерного случайного вектора называется симметрическая матрица, составленная из коэффициентов корреляции соответствующих пар компонент случайного вектора:

,

vk.com/club152685050 | vk.com/id446425943

17. Корреляционный момент и его свойства. В коэффициент корреляции (доказательства, что - |≤rxy≤| и rxy=±1, если линейная зависимость между случайными величинами).

Свойства коэффициента корреляции:

Неравенство Коши — Буняковского:

если принять в качестве скалярного произведения двух случайных величин

ковариацию , то норма случайной величины будет равна , и следствием неравенства Коши — Буняковского будет:

.

Коэффициент корреляции равен тогда и только тогда, когда X и Y линейно зависимы (исключая события нулевой вероятности, когда несколько точек «выбиваются» из прямой, отражающей линейную зависимость случайных величин):

,

где . Более того в этом случае знаки 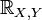и k совпадают:

.

Если X,Y независимые случайные величины, то . Обратное в общем случае неверно.

Момент корреляции:

Корреляционным моментом системы двух случайных величин называется второй смешанный центральный момент:

Для дискретных случайных величин:

для непрерывных случайных величин:

Коэффициент корреляции:

Как мы знаем, если и - независимые случайные величины, то по свойству математического ожидания (§ 4, п. 1)

vk.com/club152685050 | vk.com/id446425943

Если же и не являются независимыми случайными величинами, то, вообще говоря,

Условились за меру связи (зависимости) двух случайных величин и принять безразмерную величину , определяемую соотношением.

и называемую коэффициентом корреляции.

Рассмотрим некоторые свойства коэффициента корреляции.

Если и - независимые случайные величины, то коэффициент корреляции равен нулю.

Это свойство непосредственно вытекает из соотношений (72) и (73). Заметим, что обратное утверждение, вообще говоря, неверно, т. е. если , то отсюда еще не следует, что и независимы.

Заметим без доказательства, что . При этом если , то между случайными величинами и имеет место функциональная, а именно линейная зависимость.

Замечание. Как мы видели (§ 3, п. 6), двумерная случайная величина распределена нормально, если плотность распределения системы величин и имеет вид

Можно показать, что постоянная R равна коэффициенту корреляции величин и , т.е. . Следует заметить, что в случае, когда система величин и распределена нормально и коэффициент корреляции , то величины и независимы

vk.com/club152685050 | vk.com/id446425943

18. Плотность распределения функций случайного аргумента (на примере нормального закона распределения).

Определение 10.1.

Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргу-

мента Х:

Y = φ(X).

Выясним, как найти закон распределения функции по известному закону распределения аргумента.

1) Пусть аргумент Х – дискретная случайная величина, причем различным значениям Х соответствуют различные значения Y. Тогда вероятности соответствующих значений Х и Y равны. Пример 1. Ряд распределения для Х имеет вид:

(при вычислении значений Y в формулу, задающую функцию, подставляются возможные значения Х).

2) Если разным значениям Х могут соответствовать одинаковые значения Y, то вероятности значений аргумента, при которых функция принимает одно и то же значение, складываются. Пример 2. Ряд распределения для Х имеет вид:

(так как Y = 0 при Х = 0 и Х = 2, то р(Y = 0) = р( Х = 0) + р(Х = 2) = 0,1 + 0,3 = 0,4 ).

3) Если Х – непрерывная случайная величина, Y = φ(X), φ(x) – монотонная и дифференцируемая функция, а ψ(у) – функция, обратная к φ(х), то плотность распределения g(y) случайно функции

Y равна:

g( y) f (y( y)) |y ( y) | .

vk.com/club152685050 | vk.com/id446425943

19. Равномерный закон распределения и его числовые характеристики.

распределения вероятностей постоянна на данном отрезке. Тогда плотность распределения (ПР) f(x) и функция распределения (ФР) F(x) будут иметь следующий вид:

Это распределение реализуется в опытах, где наудачу ставится точка на отрезке [a, b], а также в экспериментах по измерению тех или иных физических величин с округлением (Х- ошибка округления).

vk.com/club152685050 | vk.com/id446425943

Наивероятнейшее число наступлений события A в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p, удовлетворяет неравенству

np-q≤m0≤np+p. Это означает, что мода случайной величины, распределённой по биномиальному закону, - число целое - находится из того же неравенства np-q≤M0(X)≤np+p.

Биномиальный закон широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и в других областях.