Теория вероятности. Билеты и ответы
.pdf
vk.com/club152685050 | vk.com/id446425943
21. Закон распределения Пуассона и его числовые характеристики.
Дискретная случайная величина X имеет закон распределения Пуассона, если она принимает значения 0, 1, 2,
..., m, ... (бесконечное, но счётное множество значений) с вероятностями
где m=0, 1, 2, ...
Ряд распределения закона Пуассона имеет вид:
|
xi |
|
0 |
|
1 |
|
2 |
|
... |
|
m |
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
|
|
|
|
|
|
... |
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что определение закона Пуассона корректно, так как основное свойство ряда распределения 
выполнено, ибо сумма ряда
(учтено, что в скобках записано разложение в ряд функции 
при
).
На рисунке приведены многоугольники (полигоны) распределения случайной величины X, имеющей закон распределения Пуассона с параметром 
(для 
=0,5; 1; 2; 3,5; 5).
Теорема. Математическое ожидание и дисперсия случайной величины X, распределённой по закону Пуассона, совпадают и равны значению параметра 
этого закона, т. е.
vk.com/club152685050 | vk.com/id446425943
При условии 
закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность p события A вкаждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Наряду с "предельным" случаем биномиального распределения закон Пуассона может возникнуть и в ряде других случаев. Так для простейшего потока событий число событий, попадающих на произвольный отрезок времени, есть случайная величина, имеющая пуассоновское распределение. Также по закону Пуассона распределены, например, число рождения четверней, число сбоев на автоматической линии, число отказов сложной системы в "нормальном режиме", число "требований на обслуживание", поступивших в единицу времени в системах массового обслуживания, и др.
Замечание. Если случайная величина представляет собой сумму двух независимых случайных величин, распределённых по закону Пуассона, то она также распределена по закону Пуассона.
vk.com/club152685050 | vk.com/id446425943
22. Нормальный закон распределения и его числовые характеристики.
СВНТ называется распределенной по нормальному (гауссовскому) закону с параметрами m Î R и s > 0, если ПР задается формулой:
|
1 |
|
|
ì |
|
f(x) = |
|
× exp |
ï- |
||
|
|
|
|||
|
|
||||
|
σ 2π |
|
|
ï |
|
|
|
|
|
|
î |
(x - m ) |
2 |
ü |
|
|
ï |
-¥ < x < +¥. |
|
|
|
ý |
|
2 ×σ 2 |
|
||
|
ï |
|
|
|
|
þ |
|
Тогда ПР f(x) и ФР F(x) такой СВ имеют следующий вид:
Ф(х) =
Для краткости говорят, что СВ Х подчиняется закону N(m, σ), т.е. Х ~ N(m, s). Параметры m и s совпадают с основными характеристиками распределения: m = mX, s = sХ = 
DX . Если СВ Х ~ N(0, 1), то она называется
стандартизованной нормальной величиной. Функция Распределения стандартизованной нормальной величиной называется функцией Лапласа и обозначается как Ф(x). С ее помощью можно вычислять
интервальные вероятности для нормального распределения N(m, s): |
|
|
||||||
|
æ x2 |
- mö |
æ x1 |
- mö |
||||
P(x1 £ |
X < x2) = Ф ç |
|
|
÷ |
- Ф ç |
|
|
÷ . |
|
|
|
|
|||||
|
è |
|
σ ø |
è |
|
σ ø |
||
При решении задач на нормальное распределение часто требуется использовать табличные значения функции Лапласа. Поскольку для функции Лапласа справедливо соотношение Ф(-х) = 1 - Ф(х), то достаточно иметь табличные значения функции Ф(х) только для положительных значений аргумента.
Для вероятности попадания на симметричный относительно математического ожидания интервал справедлива формула: P( |X - mX| < e ) = 2×Ф(e/s) - 1.
Центральные моменты нормального распределения удовлетворяют рекуррентному соотношению: mn+2 = (n+1)s2mn, n = 1, 2, ... . Отсюда следует, что все центральные моменты нечетного порядка равны нулю (так как m1 = 0).
vk.com/club152685050 | vk.com/id446425943
23. Понятие распределения χ2 и Стьюдента, и графический вид.
Распределение Стьюдента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений.
Определение:
Пусть 
— независимые стандартные нормальные случайные величины, такие что 
. Тогда распределение случайной величины 
, где
называется распределением Стьюдента с 
степенями свободы. Пишут 
. Её распределение абсолютно непрерывно и имеет плотность
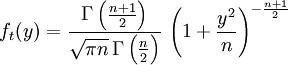, где 
— гамма-функция Эйлера.
Свойства распределения Стьюдента:
Распределение Стьюдента симметрично. В частности если 
, то 
.
Моменты:
Случайная величина 
имеет только моменты порядков 
, причём
, если 
нечётно;
, если 
чётно. В частности,
,
, если 
.
Моменты порядков 
не определены.
Связь с другими распределениями:
vk.com/club152685050 | vk.com/id446425943
Распределение Коши является частным случаем распределения Стьюдента:
.
Распределение Стьюдента сходится к стандартному нормальному при 
. Пусть дана последовательность случайных величин 
, где 
. Тогда
по распределению при 
.
Квадрат случайной величины, имеющей распределение Стьюдента, имеет распределение Фишера. Пусть t˜t(n). Тогда t2˜F(1,n).
Применение распределения Стьюдента:
Распределение Стьюдента используется в статистике для точечного оценивания, построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения. В частности, пусть 
независимые случайные величины, такие
что 
. Обозначим 
выборочное среднее этой выборки, а S2 еёвыборочную дисперсию. Тогда
.
Плотность вероятности: |
Функция распределения: |
vk.com/club152685050 | vk.com/id446425943
24. Неравенство Чебышева. Теорема Чебышева (обобщения).
.
Неравенство:
На практике сложно сказать какое конкретное значение примет случайная величина, однако, при воздействии большого числа различных факторов поведение большого числа случайных величин практически утрачивает случайный характер и становится закономерным.
Этот факт очень важен на практике, т.к. позволяет предвидеть результат опыта при воздействии большого числа случайных факторов.
Однако, это возможно только при выполнении некоторых условий, которые определяются законом больших чисел. К законам больших чисел относятся теоремы Чебышева (наиболее общий случай) и теорема Бернулли (простейший случай), которые будут рассмотрены далее.
Рассмотрим дискретную |
случайную |
величину Х (хотя |
все сказанное ниже будет справедливо и для |
||||
непрерывных случайных величин), заданную таблицей распределения: |
|||||||
|
|
|
|
|
|
|
|
|
X |
x1 |
x2 |
… |
|
xn |
|
|
|
|
|
|
|
|
|
|
p |
p1 |
p2 |
… |
|
pn |
|
|
|
|
|
|
|
|
|
Требуется определить вероятность того, что отклонение значения случайной величины от ее математического ожидания будет не больше, чем заданное число e.
Теорема. (Неравенство Чебышева) Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше чем .
Пусть случайная величина 
определена на вероятностном пространстве 
, и её математическое ожидание μ и дисперсия σ2 конечны. Тогда
, где a > 0.
Если a = kσ, где σ — стандартное отклонение и k > 0, то получаем
.
В частности, случайная величина с конечной дисперсией отклоняется от среднего больше, чем на 2 стандартных отклонения с вероятностью меньше 25%. Она отклоняется от среднего на 3 стандартных отклонения с вероятностью меньше 11,2%.
Теорема:
Если Х1, Х2, …, Хn- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное числоe, вероятность неравенства
vk.com/club152685050 | vk.com/id446425943
будет сколь угодно близка к единице, если число случайных величин достаточно велико.
Т.е. можно записать: 
(при любом 
и 
) верно при весьма общих предположениях:
Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается:
Дробь, входящая в записанное выше выражение есть не что иное как среднее арифметическое возможных значений случайной величины.
Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.
Отклоняясь от математического ожидания как в положительную так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.
Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.
vk.com/club152685050 | vk.com/id446425943
25. Следствие 1 (теорема Чебышева) и следствие 2 (теорема Бернулли) из теоремы Чебышева.
Теорема Бернулли:
Если Вероятность ρ наступления события Α в каждом испытании постоянна, то вероятность Pk,n того, что событие A наступит k раз в n независимых испытаниях, равна: 
где q = 1-p
Докаказательство:
Так как в результате n независимых испытаний, проведенных в одинаковых условиях, событие A наступает с вероятностью , следовательно противоположное ему событие с вероятностью 
.
Обозначим Ai — наступление события A в испытании с номером i. Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате n опытов событие A наступает k раз, тогда остальные n − k − раз это событие не наступает. Событие A может появиться k раз в n испытаниях в различных комбинациях, число которых равно количеству сочетаний из n элементов по k. Это количество сочетаний находится по формуле:
.
При этом вероятность каждой комбинации равна произведению вероятностей:
.
Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли: 
где q = 1-p
= Эта теорема скорее всего не так, правильные скорее всего, которые внизу!
-----------------------------------------------------------------------------------------------------------------------------------------------------------
Теорема Чебышева:
Пусть случайные величины 
последовательности (2) таковы, что:
1)Они попарно независимы.
2)Имеют конечное математическое ожидание.
3)Имеют равномерно ограниченные дисперсии 
Тогда к последовательности применим закон больших чисел.
Доказательство:
Оценим дисперсию:
vk.com/club152685050 | vk.com/id446425943
Применим неравенство (1):
Левую часть выразим через вероятность противоположного события:
Умножим обе части на (-1):
С другой стороны:
На основании двух предыдущих формул получаем формулу (3)
Теорема Бернулли:
Относительная частота события “А” в вероятностном смысле сходится к вероятности этого события:
(4)
Доказательство:
С каждым испытанием свяжем случайную величину 
.
Тогда число наступлений события “А” в “n” независимых испытаний будет равно:
vk.com/club152685050 | vk.com/id446425943
Покажем, что к этой последовательности применим закон больших чисел (равенство 3). Проверим выполнение условий теоремы Чебышева:
1) 
– попарно независимы.
2) 
3) 
Таким образом в силу теоремы Чебышева к последовательности случайных величин {
} применим закон больших чисел, выражаемый равенством (3). В данном случае среднее арифметическое:
– относительная частота.
В силу (3) получаем равенство (4).
Теорема доказана.