Теория вероятности. Билеты и ответы

vk.com/club152685050 | vk.com/id446425943

7. Случайная величина. Ее задание.

Случайной величиной называется числовая переменная величина, принимающая в зависимости от случая те или иные значения с определёнными вероятностями. Число попаданий в цель при данном числе выстрелов, скорость молекулы газа являются типичными примерами случайных величин.

Для задания случайной величины нужно знать множество всевозможных её значений и вероятности, с которыми эта случайная величина принимает свои значения. Все эти данные образуют закон распределения случайной величины или распределение вероятности.

Будем называть две случайные величины x и y взаимно независимыми, если события x = xi и y = yj являются взаимно независимыми.

Пример:

Найти закон распределения числа очков, которые выбивает стрелок на мишени, если вероятность его попадания в область 1 равна 0, вероятность попадания в область 2 равна 0,2, а в область 3 – 0,8.

Закон распределения можно представить в виде следующей таблицы:

vk.com/club152685050 | vk.com/id446425943

8. Функция распределения и ее свойства.

Рассмотрим функцию F(х), определенную на всей числовой оси следующим образом: для

каждого х значение F(х) равно вероятности того, что дискретная случайная величина примет значение, меньшее х, т. е.

Эта функция называется функцией распределения вероятностей, или кратко, функцией распределения.

Рассмотрим основные свойства функции распределения.

1) Функция распределения является неубывающей.

В самом деле, пусть <. Так как вероятность любого события неотрицательна, то . Поэтому из формулы (19) следует, что 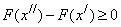, т.е. .

2) Значения функции распределения удовлетворяют неравенствам .

Это свойство вытекает из того, что F(x) определяется как вероятность. Ясно, что * 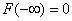и .

3) Вероятность того, что дискретная случайная величина примет одно из возможных значений xi, равна скачку функции распределения в точке xi.

Действительно, пусть xi - значение, принимаемое дискретной случайной величиной, и . Полагая , , получим: В пределе при вместо вероятности попадания случайной величины на интервал

получим вероятность того, что величина примет данное значение xi:

C другой стороны, получаем:

, т.е. предел функции F(x) справа, так как .

vk.com/club152685050 | vk.com/id446425943

9. Функция плотности распределения и ее свойства.

Функцией распределения (ФР) (или интегральным законом распределения) СВ X называется числовая функция F(x) = P{X < x}, определенная для любых x Î R.

Свойства ФР:

1.0 £ F(x) £ 1;

2.F(x1) £ F(x2), если x1 < x2, т.е. F(x) - неубывающая функция;

4. P{a £ X < b} = F(a) - F(b).

Плотностью распределения (ПР) (или дифференциальным законом распределения) СВ X называется

числовая функция f(x), равная производной от ФР, если такая производная существует: f(x) = F¢(x). Связь между ПР и ФР можно представить в интегральной форме:

b

òf (τ)×dτ =F (b)-F (a), что позволяет определить ФР:

a

x

F (x )= ò f (τ )×dτ .

- ¥

Свойства ПР:

1. f(x) ³ 0, т.к. ФР - неубывающая функция;

+∞

2. òf (τ)×dτ=1, - условие нормировки

-¥

vk.com/club152685050 | vk.com/id446425943

10. Случайная многомерная величина. Функция распределения и плотности распределения случайных многомерных величин.

Пусть имеется пространство элементарных событий U, на нем построено поле событий и для каждого события А из этого поля определена вероятность Р(А). Каждому элементарному событию gi из U сопоставим несколько чисел: ξ i1 , ξ i2 , ξ i3 , ... ξ ik или вектор ξi. Потребуем, чтобы для любых хj ( -∞ < хj <+∞ ) , j = 1, 2

... k , множество А тех g , для которых ξ j < хj ( j = 1, 2, ... k) , принадлежало полю событий, т.е. для него определена вероятность Р{ ξ 1 < x1 , ξ 2 < x2 , ... ξ k < xk } = P(A) = F( x1, x2, ... xk ). Тогда ξ называется многомерной случайной величиной, или случайным вектором, а F( x1, x2, ... xk ) ее функцией распределения.

Свойства многомерной функции распределения:

1 . F( x1, x2, ... -∞ ... xk ) = 0,2 . F( x1, x2, ... xk-1, ∞) = F( x1, x2, ... xk-1 ), т.е. если один из аргументов принимает значение ∞, то размерность случайной величины уменьшается на 1.

3 . F( x1, x2, ... xk ) не убывающая функция любого аргумента

Многомерные случайные величины могут быть непрерывными, т.е. принимать любые значения в некоторой области к-мерного пространства (например, упомянутые выше компоненты скорости молекулы). У них F( x1, x2, ... xk ) непрерывная функция всех аргументов. Для них определена к-мерная плотность распределения p( x1, x2, ... xk ), которая есть производная от функции распределения.

(7.1)

Вероятность того, что случайный вектор примет значение, лежащее в области V к-мерного пространства, равна интегралу по этой области от к-мерной плотности распределения.

Интеграл по всем переменным от - ∞ до + ∞ от к-мерной плотности распределения равен 1.

Интеграл по одной переменной от - ∞ до + ∞ от к-мерной плотности распределения равен плотности распределения (к-1)-мерной случайной величины.

Пример:

(7.2)

Многомерные случайные величины могут быть дискретными, т.е. каждая компонента случайного вектора может принимать только конечное или счетное множество определенных значений.

vk.com/club152685050 | vk.com/id446425943

11. Функция распределения системы двух случайных величин.

Функцией распределения системы двух случайных величин называется функция двух аргументов F(x, y), равная вероятности совместного выполнения двух неравенств X<x, Y<y.

Отметим следующие свойства функции распределения системы двух случайных величин:

1)Если один из аргументов стремится к плюс бесконечности, то функция распределения системы стремится к функции распределения одной случайной величины, соответствующей другому аргументу.

2)Если оба аргумента стремятся к бесконечности, то функция распределения системы стремится к единице.

3)При стремлении одного или обоих аргументов к минус бесконечности функция распределения стремится к нулю.

4)Функция распределения является неубывающей функцией по каждому аргументу.

5)Вероятность попадания случайной точки (X, Y) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по

формуле:

vk.com/club152685050 | vk.com/id446425943

12. Вероятность попадания случайных величин в прямоугольник.

Вероятность попадания случайной точки в полуполосу:

Используя функцию распределения системы случайных величин X и Y, легко найти вероятность того, что в результате испытания случайная точка попадет в полуполосу x1 < X < x2, Y < y или в полуполосу X < x и y1 < Y < y2.

Вычитая из вероятности попадания случайной точки в квадрант с вершиной (x2, y) вероятность попадания точки в квадрант с вершиной (x1, y) , получим P(x1 ≤ X < x2, Y < y) = F(x2 ,y) - F(x1 ,y).

Аналогично имеем:

P(X< x, y1 ≤ Y < y2) = F(x, y2 ) - F(x, y1).

Таким образом, вероятность попадания случайной величины в полуполосу равна приращению функции распределения по одному из аргументов.

Рассмотрим прямоугольник ABCD (A(x1,y2), B(x2,y2), C(x1,y1), D(x2,y1)) со сторонами, параллельными координатным осям. Пусть уравнения сторон:

X = x1, X = x2, Y = y1 и Y = y2 .

Найдем вероятность попадания случайной точки (X;Y) в этот прямоугольник. Искомую вероятность можно найти, например, так: из вероятности попадания случайной точки в полуполосу AB (эта вероятность равна F(x2 ,y2) - F(x1 ,y1)) вычесть вероятность попадания точки в полуполосу CD (эта вероятность равна F(x2 ,y1) - F(x1 ,y1)):

P(x1 ≤ X < x2 , y1 ≤ Y < y2) = [F(x2 ,y2) - F(x1 ,y2)] – [F(x2 ,y1) - F(x1 ,y1)].

vk.com/club152685050 | vk.com/id446425943

13. Условные законы распределения. Связь одномерной и двумерной функции плотности распределения.

Как было показано выше, зная совместный закон распределения можно легко найти законы распределения каждой случайной величины, входящей в систему.

Однако, на практике чаще стоит обратная задача – по известным законам распределения случайных величин найти их совместный закон распределения.

В общем случае эта задача является неразрешимой, т.к. закон распределения случайной величины ничего не говорит о связи этой величины с другими случайными величинами.

Кроме того, если случайные величины зависимы между собой, то закон распределения не может быть выражен через законы распределения составляющих, т.к. должен устанавливать связь между составляющими.

Все это приводит к необходимости рассмотрения условных законов распределения.

Определение. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения.

Условный закон распределения можно задавать как функцией распределения так и плотностью распределения.

Условная плотность распределения вычисляется по формулам:

Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.

Если известна плотность распределения, то функция распределения может быть легко найдена по формуле:

Двумерная плотность распределения неотрицательна и двойной интеграл с бесконечными пределами от двумерной плотности равен единице.

По известной плотности совместного распределения можно найти плотности распределения каждой из составляющих двумерной случайной величины.

vk.com/club152685050 | vk.com/id446425943

14. Числовые характеристики одномерной случайной величины.

Некоторые числовые характеристики одномерных случайных величин: начальные и центральные моменты, мода, медиана, квантиль, коэффициенты асимметрии и эксцесса. Числовые характеристики двумерных случайных величин: начальные и центральные моменты. Корреляционный момент и коэффициент корреляции. Коррелированность и зависимость случайных величин.

В частности, μ1 = M(Х – М(Х)) = 0, μ2 = M((Х – М(Х))2) = D(X).

Можно получить соотношения, связывающие начальные и центральные моменты:

иногда характеристикой положения, так как она дает представление о положении случайной величии-ны на числовой оси. Другими характеристиками положения являются мода и медиана.

Пример 1.

Если ряд распределения дискретной случайной величины Х имеет вид:

то М = 2.

Пример 2.

vk.com/club152685050 | vk.com/id446425943

Замечание 1. Если кривая распределения имеет больше одного максимума, распределение называется полимодальным, если эта кривая не имеет максимума, но имеет минимум – анти-модальным.

Замечание 2. В общем случае мода и математическое ожидание не совпадают. Но, если распре-деление является симметричным и модальным (то есть кривая распределения симметрична от-носительно прямой х = М) и имеет математическое ожидание, оно совпадает с модой.

Определение 9.4. Медианой Ме непрерывной случайной величины называют такое ее значение, для которого

Графически прямая х = Ме делит площадь фигуры, ограниченной кривой распределения, на две равные части.

Замечание. Для симметричного модального распределения медиана совпадает с математичес-ким ожиданием и модой.

Определение 9.5. Для случайной величины Х с функцией распределения F(X) квантилью порядка р (0 < p < 1) называется число Кр такое, что F(Kp) ≤ p, F(Kp + 0) ≥ p. В частности, еслиF(X) строго монотонна, Кр: F(Kp) = p.

Асимметрия и эксцесс

Если распределение не является симметричным, можно оценить асимметрию кривой распреде-ления с помощью центрального момента 3-го порядка. Действительно, для симметричного распределения все нечетные центральные моменты равны 0 ( как интегралы от нечетных функ-ций в симметричных пределах), поэтому выбран нечетный момент наименьшего порядка, не тождественно равный 0. Чтобы получить безразмерную характеристику, его делят на σ3 (так как μ3 имеет размерность куба случайной величины).

Определение 9.6. Коэффициентом асимметрии случайной величины называется

В частности, для кривой, изображенной на рис.1, Sk > 0, а на рис.2 - Sk < 0.

Для оценки поведения кривой распределения вблизи точки максимума (для определения того, насколько «крутой» будет его вершина) применяется центральный момент 4-го порядка.

vk.com/club152685050 | vk.com/id446425943

Определение 9.7. Эксцессом случайной величины называется величина

(9.5)

Замечание. Можно показать, что для нормального распределения , и, соответственно, Ех = 0. Для кривых с более острой вершиной Ех >0, в случае более плоской вершины Ех < 0.