
Теория вероятности. Билеты и ответы
.pdf
vk.com/club152685050 | vk.com/id446425943
26. Понятие выборки. Вариационный ряд. Полигон частот. Выборочная функция распределения. Гистограмма.
Понятие выборки - одно из основных в комбинаторике, теории вероятностей и математической статистике, а подсчет числа выборок исторически был одной из первых задач комбинаторики. В типичных задачах по теории вероятностей подсчитывается число различных вариантов (выборок), а через них и вероятностей событий, связанных в большинстве случаев с бросанием монеты, кубика или со случайным выбором шаров из урны. Одним из первых занялся подсчетом различных комбинаций при игре в кости итальянский математик Тарталья. Приведем здесь одну из таких задач.
Пример 1. На какую сумму очков, выпадающих при подбрасываниях двух костей, разумно сделать ставку?
Решение. Перечислим возможные суммы и способы их получения.
2 = 1 + 1; 3 = 1 + 2 = 2 + 1; 4 = 1 + 3 = 3 + 1 = 2 + 2; 5 = 1 + 4 = 4 + 1 = 2 + 3 = 3 + 2;
6 = 1 + 5 = 5 + 1 = 2 + 4 = 4 + 2 = 3 + 3; 7 = 1 + 6 = 6 + 1 = 2 + 5 = 5 + 2 = 4 + 3 = 3 + 4;
8 = 2 + 6 = 6 + 2 = 3 + 5 = 5 + 3 = 4 + 4; 9 = 3 + 6 = 6 + 3 = 4 + 5 = 5 + 4;
10 = 4 + 6 = 6 + 4 = 5 + 5; 11 = 5 + 6 = 6 + 5; 12 = 6 + 6.
Откуда видно, что целесообразно сделать ставку на выпадение в сумме 7 очков, поскольку она получается наибольшим количеством вариантов, а, следовательно, имеет больше шансов на выпадение, чем другие суммы. Первоначально комбинаторные задачи касались в основном азартных игр - определения, сколькими способами можно получить данное число очков, бросая несколько костей, как в предыдущем примере, или сколькими способами можно получить тот или иной набор карт. Размышления над анализом азартных игр явились движущей силой в развитии комбинаторики и развивавшейся одновременно с ней теорией вероятностей. Такой подход логично продолжить и для рассмотрения современных игр.
Вариационный ряд
Вариационный ряд — упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины:
равные между собой элементы выборки нумеруются в произвольном порядке; элементы вариационного ряда называются порядковыми (ранговыми) статистиками; число λm =m / n называется рангом порядковой
статистики 
Вариационный ряд используется для построения эмпирической функции распределения. Если элементы вариационного ряда независимы и имеют общую плотность распределения f, то совместная плотность распределения элементов вариационного ряда имеет вид:
Полигон частот и гистограмма

vk.com/club152685050 | vk.com/id446425943
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Полигоном частот называют ломаную линию, отрезки которой соединяют точки  . Для построения полигона частот на оси абсцисс откладывают варианты
. Для построения полигона частот на оси абсцисс откладывают варианты 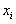 , а на оси ординат –
, а на оси ординат –
соответствующие им частоты  и соединяют точки
и соединяют точки  отрезками прямых.
отрезками прямых.
Полигон относительных частот строится аналогично, за исключением того, что на оси ординат откладываются относительные частоты  .
.
В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для
каждого частичного интервала  – сумму частот вариант, попавших в i–й интервал.
– сумму частот вариант, попавших в i–й интервал.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой
служат частичные интервалы длиною h, а высоты равны отношению  . Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси
. Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси
абсцисс на расстоянии (высоте)  . Площадь i–го прямоугольника равна
. Площадь i–го прямоугольника равна  – сумме частот вариант i–о интервала, поэтому площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
– сумме частот вариант i–о интервала, поэтому площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
В случае гистограммы относительных частот по оси ординат откладываются относительные частоты  , на оси абсцисс – частичные интервалы, над ними проводят отрезки, параллельные оси абсцисс на высоте
, на оси абсцисс – частичные интервалы, над ними проводят отрезки, параллельные оси абсцисс на высоте 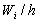 .
.
Площадь i–го прямоугольника равна относительной частоте вариант  , попавших в i–й интервал. Поэтому площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.
, попавших в i–й интервал. Поэтому площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.
Выборочная функция распределения:
Выборочная (эмпирическая) функция распределения в математической статистике - это приближение теоретической функции распределения, построенное с помощью выборки из него.
Пусть  - выборка из распределения случайной величины
- выборка из распределения случайной величины  , задаваемого функцией распределения
, задаваемого функцией распределения  . Будем считать, что
. Будем считать, что 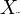 , где
, где  , -независимые случайные величины, определённые на некотором пространстве элементарных исходов Ω. Пусть
, -независимые случайные величины, определённые на некотором пространстве элементарных исходов Ω. Пусть  . Определим случайную
. Определим случайную
величину 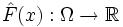 следующим образом:
следующим образом:
vk.com/club152685050 | vk.com/id446425943
 ,
,
где  - индикатор события
- индикатор события  ,
,  - функция Хевисайда. Таким образом, выборочная функция распределения в точке
- функция Хевисайда. Таким образом, выборочная функция распределения в точке  равна относительной частоте элементов выборки, не превосходящих значение
равна относительной частоте элементов выборки, не превосходящих значение 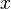 . Случайная величина
. Случайная величина  называется выборочной функцией распределения случайной величины
называется выборочной функцией распределения случайной величины 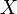 и является аппроксимацией для функции
и является аппроксимацией для функции 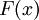 . Существует результат, показывающий, что при
. Существует результат, показывающий, что при  функция
функция  равномерно сходится к
равномерно сходится к  , и указывающий скорость сходимости.
, и указывающий скорость сходимости.

vk.com/club152685050 | vk.com/id446425943
27. Понятие оценки. Свойства оценок. Виды оценок.
Для установления качества оценки используют три основные свойства и рассматривают несмещенные оценки, состоятельные оценки и эффективные оценки.
Для того, чтобы определить эти свойства, необходимо предварительно ввести понятие статистики. Под статистикой  будем понимать функцию от выборки
будем понимать функцию от выборки  случайной величины
случайной величины  . Следует отметить, что функция
. Следует отметить, что функция 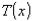 сама является случайной величиной. Если статистика
сама является случайной величиной. Если статистика  позволяет оценить
позволяет оценить
некоторую характеристику  случайной величины
случайной величины  , то говорят, что статистика
, то говорят, что статистика  оценивает
оценивает  . Например, статистика, оценивающая дисперсию случайной величины имеет вид:
. Например, статистика, оценивающая дисперсию случайной величины имеет вид:
.
Статистика  называется несмещенной оценкой параметра
называется несмещенной оценкой параметра  , если математическое ожидание оценки равняется оцениваемому параметру:
, если математическое ожидание оценки равняется оцениваемому параметру:
Статистика  называется эффективной оценкой параметра
называется эффективной оценкой параметра  , если среднеквадратическая ошибка данной оценки является наименьшей среди всех возможных оценок:
, если среднеквадратическая ошибка данной оценки является наименьшей среди всех возможных оценок:
Статистика  называется состоятельной оценкой параметра параметра
называется состоятельной оценкой параметра параметра  , если с ростом размера выборки оценка стремиться по вероятности к оцениваемому параметру:
, если с ростом размера выборки оценка стремиться по вероятности к оцениваемому параметру:
 при любом сколь угодно малом
при любом сколь угодно малом 
vk.com/club152685050 | vk.com/id446425943
28. Точечные оценки. Принцип максимального правдоподобия.
Точечная оценка в математической статистике — это число, вычисляемое на основе наблюдений, предположительно близкое к оцениваемому параметру.
Пусть  — случайная выборка из распределения, зависящего от параметра
— случайная выборка из распределения, зависящего от параметра  .
.
Тогда статистику  , принимающую значения в
, принимающую значения в  , называют точечной оценкой параметра θ
, называют точечной оценкой параметра θ
Замечание:
Формально статистика  может не иметь ничего общего с интересующим нас значением параметра θ. Её полезность для получения практически приемлемых оценок вытекает из дополнительных свойств, которыми она обладает или не обладает.
может не иметь ничего общего с интересующим нас значением параметра θ. Её полезность для получения практически приемлемых оценок вытекает из дополнительных свойств, которыми она обладает или не обладает.
Свойства точечных оценок:
- Оценка  называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности:
называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности:
 ,
,
где  обозначает математическое ожидание в предположении, что θ — истинное значение параметра (распределения выборки X).
обозначает математическое ожидание в предположении, что θ — истинное значение параметра (распределения выборки X).
-Оценка  называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.
называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.
-Оценка  называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности:
называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности:  ,
,
 по вероятности при
по вероятности при  .
.
- Оценка  называется сильно состоятельной, если
называется сильно состоятельной, если  ,
,  почти наверное при
почти наверное при  .
.
Метод максимального правдоподобия (также метод наибольшего правдоподобия) в математической статистике — это метод оценивания неизвестного параметра путём максимизации функции правдоподобия. Основан на предположении о том, что вся информация о статистической выборке содержится в функции правдоподобия. Метод максимального правдоподобия был проанализирован, рекомендован и значительно популяризирован Р. Фишером между 1912 и 1922 годами (хотя ранее он был использован Гауссом, Лапласом и другими).
Оценка максимального правдоподобия является популярным статистическим методом, который используется для создания статистической модели на основе данных, и обеспечения оценки параметров модели.

vk.com/club152685050 | vk.com/id446425943
Метод максимального правдоподобия соответствует многим известным методам оценки в области статистики. Например, предположим, что вы заинтересованы ростом жителей Украины. Предположим, у вас данные роста некоторого количества людей, а не всего населения. Кроме того предполагается, что рост является нормально распределенной величиной с неизвестной дисперсией и средним значением. Среднее значение и дисперсия роста выборки является максимально правдоподобным к среднему значению и дисперсии всего населения.
Для фиксированного набора данных и базовой вероятностной модели, используя метод максимального правдоподобия, мы получим значения параметров модели, которые делают данные «более близкими» к реальным. Оценка максимального правдоподобия дает уникальный и простой способ определить решения в случае нормального распределения.
Метод оценки максимального правдоподобия применяется для широкого круга статистических моделей, в том числе:
линейные модели и обобщенные линейные модели;
факторный анализ;
моделирования структурных уравнений;
многие ситуации, в рамках проверки гипотезы и доверительного интервала формирования;
дискретные модели выбора.
Определение:
Пусть есть выборка 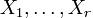 из распределения
из распределения  , где
, где  — неизвестный параметр. Пусть
— неизвестный параметр. Пусть  — функция правдоподобия, где
— функция правдоподобия, где 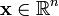 .Точечная оценка
.Точечная оценка
называется оце́нкой максима́льного правдоподо́бия параметра θ. Таким образом оценка максимального правдоподобия — это такая оценка, которая максимизирует функцию правдоподобия при фиксированной реализации выборки.
Замечание:
- Так как функция  монотонно возрастает на всей области определения, максимум любой функции f(θ) является максимумом функции lnf(θ), и наоборот. Таким образом
монотонно возрастает на всей области определения, максимум любой функции f(θ) является максимумом функции lnf(θ), и наоборот. Таким образом
 ,
,
где L — логарифмическая функция правдоподобия.
- Оценка максимального правдоподобия, вообще говоря, может быть смещённой (см. примеры).
Примеры:

vk.com/club152685050 | vk.com/id446425943
Пусть  — независимая выборка из непрерывного равномерного распределения на отрезке [0,θ], где θ > 0 — неизвестный параметр. Тогда функция правдоподобия имеет вид
— независимая выборка из непрерывного равномерного распределения на отрезке [0,θ], где θ > 0 — неизвестный параметр. Тогда функция правдоподобия имеет вид
Последнее равенство может быть переписано в виде:
где  , откуда видно, что своего максимума функция правдоподобия достигает в точке
, откуда видно, что своего максимума функция правдоподобия достигает в точке  . Таким образом
. Таким образом
.
Пусть  — независимая выборка из нормального распределения с неизвестными средним и дисперсией. Построим оценку максимального правдоподобия
— независимая выборка из нормального распределения с неизвестными средним и дисперсией. Построим оценку максимального правдоподобия 
для неизвестного вектора параметров  . Логарифмическая функция правдоподобия принимает вид:
. Логарифмическая функция правдоподобия принимает вид:
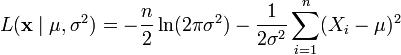 .
.
Чтобы найти её максимум, приравняем к нулю частные производные:
откуда
— выборочное среднее, а  — выборочная дисперсия.
— выборочная дисперсия.

vk.com/club152685050 | vk.com/id446425943
29. Интервальное оценивание. Интервальные оценки математического ожидания и дисперсии.
Интервальное оценивание — один из видов статистического оценивания, предполагающий построение интервала, в котором с некоторой вероятностью находится истинное значение оцениваемого параметра.
Определение:
Пусть  - неизвестный параметр генеральной совокупности. По сделанной выборке по определенным правилам находятся числа
- неизвестный параметр генеральной совокупности. По сделанной выборке по определенным правилам находятся числа  и
и  такие чтобы выполнялось неравенство:
такие чтобы выполнялось неравенство:
Интервал  является доверительным интервалом для параметра
является доверительным интервалом для параметра  , а число
, а число  - доверительной вероятностью или надежностью сделанной оценки. Обычно надежность задается заранее, причем выбираются числа близкие к 1 (0.95, 0.99 или 0.999).
- доверительной вероятностью или надежностью сделанной оценки. Обычно надежность задается заранее, причем выбираются числа близкие к 1 (0.95, 0.99 или 0.999).
Интервальная оценка математического ожидания при известной дисперсии
Итак, Х ~ N(а,σ) (случайная величина Х имеет нормальное распределение с параметрами а и σ), причем значение параметра а не известно, а значение дисперсии σ2 известно.
При  ~
~ эффективной оценкой параметра а является
эффективной оценкой параметра а является  , при этом
, при этом  ~
~ .
.
Статистика  имеет распределениеN(0; 1) независимо от значения параметра а и как функция параметра а непрерывна и строго монотонна. Следовательно, с учетом неравенства (1.12) и симметричности двусторонних критических границ распределения N(0; 1) будем иметь:
имеет распределениеN(0; 1) независимо от значения параметра а и как функция параметра а непрерывна и строго монотонна. Следовательно, с учетом неравенства (1.12) и симметричности двусторонних критических границ распределения N(0; 1) будем иметь:
Р(–uа < Z < uа) = 1 – α = γ.
Решая неравенство  относительно а, получим, что с вероятностью 1 – α выполняется неравенство:
относительно а, получим, что с вероятностью 1 – α выполняется неравенство:
, |
(1.13) |
при этом: |
|
. |
(1.14) |
Число uа находят по прил. 3 из условия Ф(uа) = γ/2.
Замечание. Если п велико, оценку (1.13) можно использовать и при отсутствии нормального распределения величины Х, так как в силу следствия из центральной предельной теоремы при случайной выборке большого объема п
 .
.
В частности, если Х = μ, где μ – случайное число успехов в большом числе п испытаний Бернулли, то
 ,
,
и с вероятностью ≈1 – α для вероятности р успеха в единичном испытании выполняется неравенство
 . (1.15)
. (1.15)

vk.com/club152685050 | vk.com/id446425943
Заменяя значения р и q = 1 – р в левой и правой частях неравенства (1.15) их оценками 
и  , что допустимо при большом п,получим приближенный доверительный интервал для вероятности р:
, что допустимо при большом п,получим приближенный доверительный интервал для вероятности р:
< p < |
. |
(1.16) |
Пример:
Фирма коммунального хозяйства желает на основе выборки оценить среднюю квартплату за квартиры определенного типа снадежностью не менее 99 % и погрешностью, меньшей 10 д. е. Предполагая, что квартплата имеет нормальное распределение со средним квадратичным отклонением, не превышающим 35 д. е., найдите минимальный объем выборки.
Решение. По условию требуется найти такое п, при котором  , где а и
, где а и  – генеральная и выборочная средние.
– генеральная и выборочная средние.
Приравняв γ = 0,99, α = 1 – γ, из прил. 3 найдем число uа, при котором Ф(uа) = γ / 2 = 0,495; и0,01 = 2,6. При ε =
10 и σ = 35 из формулы (1.14) получим  . Но так как с ростом γ и
. Но так как с ростом γ и
уменьшением ε растет п, то п ≥ 82,81 и nmin = 83 (конечно, при уменьшении верхней границы для σ будет уменьшаться и nmin).

vk.com/club152685050 | vk.com/id446425943
30. Интервальные оценки математического ожидания нормально распределенной случайной величины при неизвестной дисперсии.
Интервальная оценка математического ожидания при неизвестной диcперсии
Итак, Х ~ N(а,σ), причем числовые значения ни а, ни σ2 не известны. По случайной выборке найдем эффективную оценку параметра а:  и оценку
и оценку
параметра σ2.
Построение интервальной оценки для а основано на статистике:
 ,
,
которая при случайной выборке из генеральной совокупности Х ~ N(а,σ) имеет распределение Стьюдента с (п – 1) степенью свободы независимо от значения параметра а и как функция параметра а непрерывна и строго монотонна.
С учетом неравенства (1.12) и симметричности двусторонних критических границ распределения Стьюдента будем иметь:
 . Решая неравенство:
. Решая неравенство:
относительно а, получим, что с вероятностью 1 – α выполняется неравенство:
, |
(1.17) |
и ошибка оценки  при неизвестном значении параметра σ2
при неизвестном значении параметра σ2
, |
(1.18) |
где число  находят по прил. 4 при k = п – 1 и р = α.
находят по прил. 4 при k = п – 1 и р = α.
Замечание. При k = n – 1 > 30 случайная величина t(k) имеет распределение, близкое к N(0; 1), поэтому с вероятностью ≈γ
, |
(1.19) |
где Ф(uа) = γ/2.
Пример:
Для отрасли, включающей 1200 фирм, составлена случайная выборка из 19 фирм. По выборке оказалось, что в фирме в среднем работают 77,5 человек при среднем квадратичном отклонении s = 25 человек. Пользуясь 95%-ным доверительным интервалом, оцените среднее число работающих в фирме по всей отрасли и общее
