Теория вероятности. Билеты и ответы

vk.com/club152685050 | vk.com/id446425943

число работающих в отрасли. Предполагается, что количество работников фирмы имеет нормальное распределение.

Решение. При k = п – 1 = 18 и р = γ = 0,95, α = 0,05 найдем в прил. 4

t0,05 = 2,10. Доверительный интервал (1.17) примет вид: (65,5; 89,5). С вероятностью 95 % можно утверждать, что этот интервал накроет среднее число работающих в фирме по всей отрасли. Тогда доверительный интервал для числа работающих в отрасли в целом таков: (1200 – 65,5;1200 + 89,5) или (1134,5; 1289,5).

vk.com/club152685050 | vk.com/id446425943

31. Интервальные оценки дисперсии нормально распределенной случайной величины при известном математическом ожидании.

Пусть - независимая выборка из нормального распределения, где μ -

математическое ожидание. Определим произвольное и построим α-доверительный интервал для неизвестной дисперсии σ2.

Утверждение. Случайная величина

имеет распределение χ2(n). Пусть - α-процентиль этого распределения. Тогда имеем:

.

После подстановки выражения для H и несложных алгебраических преобразований получаем:

.

vk.com/club152685050 | vk.com/id446425943

32. Критерии согласия.

Критериями согласия называют критерии, предназначенные для проверки простой гипотезы

при сложной альтернативе . Мы рассмотрим более широкий класс основных гипотез, включающий и сложные гипотезы, а критериями согласия будем называть любые критерии, устроенные по одному и тому же принципу. А именно, пусть задана некоторая функция отклонения эмпирического распределения от теоретического, распределение которой существенно разнится в зависимости от того, верна или нет основная гипотеза. Критерии согласия принимают или отвергают основную гипотезу исходя из величины этой функции отклонения.

Итак, имеется выборка из распределения . Мы сформулируем ряд понятий для случая простой основной гипотезы, а в дальнейшем будем их корректировать по мере изменения задачи.

Проверяется простая основная гипотеза при сложной альтернативе .

K1 .

Пусть возможно задать функцию , обладающую свойствами:

а)если гипотеза верна, то , где — непрерывное распределение; б)если гипотеза неверна, то при .

K2 .

Пусть такая функция задана. Для случайной величины из распределения определим постоянную из равенства .

Построим критерий:

Мы построили критерий согласия. Он «работает» по принципу: если для данной выборки функция отклонения велика (по абсолютному значению), то это свидетельствует в пользу альтернативы, и наоборот. Убедимся в том, что этот критерий имеет (асимптотический) размер 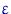и является состоятельным.

vk.com/club152685050 | vk.com/id446425943

33. Критерии согласия Пирсона.

Критерий Пирсона, или критерий χ² (Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.

Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу H0 о том, что эта

случайная величина подчиняется закону распределения F(x). Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение F *(x) исследуемой случайной величины. Сравнение эмпирического F * (x) и теоретического распределений производится с помощью специального правила — критерия согласия. Одним из таких критериев и является критерий Пирсона.

Статистика критерия:

Для проверки критерия вводится статистика:

где — предполагаемая вероятность попадания в i-й интервал, — соответствующее эмпирическое значение, ni — число элементов выборки из i-го интервала, N — полный объём выборки.

Эта величина в свою очередь является случайной (в силу случайности X) и должна подчиняться распределению χ2.

vk.com/club152685050 | vk.com/id446425943

34. Критерии согласия Колмогорова.

В статистике критерий согласия Колмогорова (также известный, как критерий согласия Колмогорова — Смирнова) используется для того, чтобы определить, подчиняются ли

два эмпирических распределения одному закону, либо определить, подчиняется ли полученное распределение предполагаемой модели.

Критерий Колмогорова — Смирнова о проверке гипотезы об однородности двух эмпирических законов распределения является одним из основных и наиболее широко используемых непараметрических методов, так как достаточно чувствителен к различиям в исследуемых выборках.

Статистика:

Эмпирическая функция распределения (ЭФР) случайной величины , построенная по выборке , имеет вид:

где указывает, попало ли наблюдение Xi в область :

Статистика критерия для эмпирической функции распределения определяется следующим образом:

Критерий:

Обозначим нулевую гипотезу , как гипотезу о том, что выборка

подчиняется распределению . Тогда по теореме Колмогорова для введённой статистики справедливо:

Учтём, что критерий имеет правостороннюю критическую область.

vk.com/club152685050 | vk.com/id446425943

35. Определение случайной функции. Законы распределения. Числовые характеристики.

Случайный процесс (случайная функция) в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим рольвремени или координаты. Другое определение:

Случайным называется процесс u(t), мгновенные значения которого являются случайными величинами.

Определение:

Пусть дано вероятностное пространство . Параметризованное семейство случайных величин

,

где T произвольное множество, называется случайной функцией.

Если , то параметр может интерпретироваться как время. Тогда случайная

функция {Xt} называется случайным процессом. Если множество T дискретно, например , то такой случайный процесс называется случа́йной после́довательностью.

Если , где , то параметр может интерпретироваться как точка в пространстве, и тогда случайную функцию называют случа́йным по́лем.

Данная классификация нестрогая. В частности, термин "случайный процесс" часто используется как безусловный синоним термина "случайная функция".

Законы распределения:

∙Биномиальный закон.

∙Закон Пуассона.

∙Геометрическое распределение.

∙Гипергеометрическое распределение.

∙Равномерный закон.

∙Показательный (экспоненциальный) закон.

∙Нормальный закон.

∙Логарифмически-нормальное распределение.

∙Функция надежности.

Числовые характеристики:

Математическое ожидание — это число, вокруг которого сосредоточены значения случайной величины.

Если x — дискретная случайная величина с распределением то ее математическим ожиданием (обозначается Mx) называется величина, вычисленная по формуле

, если число значений случайной величины конечно, и по формуле

vk.com/club152685050 | vk.com/id446425943

,если число значений случайной величины счетно. При этом, если ряд в правой части последнего равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Математическое ожидание непрерывной случайной величины с плотностью вероятностей px (x) вычисляется по формуле

.

При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Если случайная величина h является функцией случайной величины x, h = f(x ), то

.

Аналогичные формулы справедливы для функций дискретной случайной величины:

, .

При вычислении математического ожидания случайной величины полезны следующие его свойства:

∙математическое ожидание константы равно этой константе, Mc = c;

∙математическое ожидание — линейная функция случайной величины, т.е. при произвольных постоянных a и bсправедливо: M(ax +bh ) = aMx + bMh;

∙математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(xh )=Mx Mh;

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина x имеет математическое ожидание Mx, то дисперсией случайной величины x называется величина .

Легко показать, что

.

vk.com/club152685050 | vk.com/id446425943

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для

непрерывных. Величина Mx2 вычисляется по формулам , для дискретных и непрерывных случайных величин соответственно.

Еще одним параметром для определения меры разброса значений случайной величины является среднеквадратичное отклонение s x , связанное с дисперсией соотношением . Перечислим основные свойства дисперсии:

∙дисперсия любой случайной величины неотрицательна, Dx >= 0;

∙дисперсия константы равна нулю, Dc = 0;

∙для произвольной константы D(cx ) = c2Dx ;

∙дисперсия суммы двух независимых случайных величин равна сумме их дисперсий, D(x ± h ) = Dx ± Dh .

Моменты:

В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются начальные и центральные моменты.

Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x , т.е. .

Центральным моментом k-го порядка случайной величины x называется величина , определяемая формулой

.

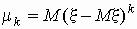Заметим, что математическое ожидание случайной величины — начальный момент первого порядка, , а дисперсия — центральный момент второго порядка, .

Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты. Одна из таких формул приведена выше: .

В дальнейшем будет использована формула

.

Нетрудно понять, что если плотность распределения вероятностей случайной величины симметрична относительно прямой x = Mx , то все ее центральные моменты нечетного порядка равны нулю.

vk.com/club152685050 | vk.com/id446425943

36. Стационарные случайные функции. Определение в «узком» и «широком» смысле. Понятие «Белого шума».

Случайный процесс (случайная функция) в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты.

Другое определение:

Случайным называется процесс u(t), мгновенные значения которого являются случайными величинами.

Определение:

Пусть дано вероятностное пространство . Параметризованное семейство случайных величин

,

где T произвольное множество, называется случайной функцией.

Терминология:

Если , то параметр может интерпретироваться как время. Тогда случайная

функция {Xt} называется случайным процессом. Если множество T дискретно, например , то такой случайный процесс называется случайной последовательностью.

Если , где , то параметр может интерпретироваться как точка в пространстве, и тогда случайную функцию называют случайным полем.

Данная классификация нестрогая. В частности, термин "случайный процесс" часто используется как безусловный синоним термина "случайная функция".

Классификация:

Случайный процесс X(t) называется процессом дискретным во времени, если система в которой он протекает, меняет свои состояния только в моменты времени t1, t2,…,tn, число которых конечно или счетно. Случайный процесс называется процессом с непрерывным временем, если переход их состояния в состояние может происходить в любой момент времени.

Случайный процесс называется процессом с непрерывными состояниями, если значением случайного процесса является непрерывная случайная величина.

Случайный процесс называется случайным процессом с дискретными состояниями, если значением случайного процесса является дискретная величина:

1.а. дискретное время, дискретное состояние, 1.б. непрерывное время, дискретное состояние, 2.а. дискретное время, непрерывное состояние, 2.б. непрерывное время, непрерывное состояние.

Случайный процесс называется стационарным, если его вероятностные закономерности неизменны во времени.

vk.com/club152685050 | vk.com/id446425943

Случайный процесс называется процессом со стационарными приращениями определенного порядка, если вероятностные закономерности такого приращения неизменны во времени. Такие процессы были рассмотрены Ягломом.

Траектория случайного процесса:

Пусть дан случайный процесс . Тогда для каждого фиксированного Xt — случайная величина. Если фиксирован элементарный исход 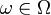, то — детерминистическая функция параметра t. Такая функция называется траекто́рией или реализа́цией случайной функции {Xt}.

Примеры:

, где называется стандартной гауссовской (нормальной) случайной последовательностью.

Пусть 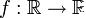, и Y — случайная величина. Тогда является случайным процессом.