1. Социальная статистика

1.1. Методические указания и решение типовых задач

Индекс реальной заработной платы исчисляется по формуле:

или (1.1)

где и – номинальная заработная плата в отчетном и базисном периодах;

– индекс потребительских цен;

– индекс номинальной заработной платы;

– индекс покупательской способности рубля.

Для оценки интенсивности изменения структуры доходов (расходов) населения, потребительских расходов домашних хозяйств по группам населения в одном из исследуемых периодов используют:

1. Линейный коэффициент структурных различий (сдвигов)

(1.2)

где и – относительные показатели структуры изучаемых совокупностей;

n – число структурных составляющих;

2. квадратический коэффициент структурных сдвигов (в том случае, если показатели измерены в процентах, )

; (1.3)

3. интегральный коэффициент К.Гатева изменяется в пределах

; (1.4)

4. индекс Салаи изменяется в пределах

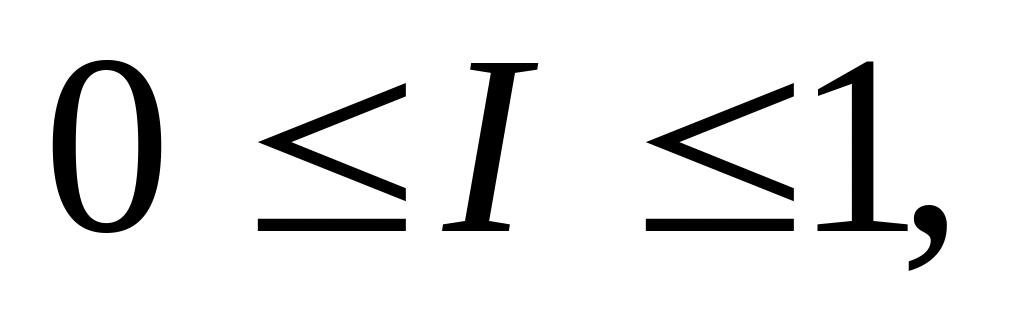
. (1.5)

Расчет агрегатного индекса физического объема потребления осуществляется по формуле

(1.6)

где , и , – количество потребленных в отчетном периоде и базисном периодах соответственно товаров и услуг.

Для изучения динамики потребления отдельных групп товаров или услуг применятся средний гармонический индекс физического объема:

, (1.7)

где – индивидуальные индексы цен на отдельные товары и услуги.

Коэффициент эластичности потребления в зависимости от изменения доходов

(1.8)

где х и y – начальные доход и потребление,

и – их приращения за некоторый период (или при переходе от одной группы к другой)

К основным доходам дифференциации доходов населения и уровня бедности относятся следующие показатели.

Коэффициент фондов

, (1.9)

где и – среднедушевой доход соответственно 10% населения с наименьшими доходами и 10% населения с самыми высокими доходами.

Можно также рассчитать по формуле

, (1.10)

где и – суммарный доход соответственно 10% самой бедной и 10% наиболее богатой частей населения.

Коэффициенты доходов и потребления населения

, (1.11)

где и соответственно девятый и первый децили.

Коэффициент концентрации доходов Джини показывает распределение всей суммы доходов населения между его отдельными группами

cum , (1.12)

где – доля населения, принадлежащая к i-й социальной группе в общей численности населения;

– доля доходов, сосредоточенная у i-й социальной группы населения;

n – число социальных групп

cum – кумулятивная доля дохода.

Коэффициент Джини можно рассчитать по кривой Лоренца как отношение площади фигуры, образуемой кривой Лоренца линией равномерного распределения к площади треугольника ниже линии равномерного распределения :

. (1.13)

Пример 1.1.1. Имеются следующие данные о распределении населения России по среднедушевому денежному доходу

Таблица 1.1

Среднедушевой денежный доход в месяц, руб	Численность населения, млн чел. f	Середина интервала		Кумулятивная частота S
1	2	3	4	5
До 100	2,9	50	145	2,9
1	2	3	4	5
100-200	18,5	150	2775	21,4
200-300	25,5	250	6375	46,9
300-400	23,4	350	8190	70,3
400-500	18,8	450	8460	89,1
500-600	14,3	550	7865	103,4
600-700	10,7	650	6955	114,1
700-800	8,0	750	6000	122,1
800-900	6,0	850	5100	128,1
900-1000	4,5	950	4275	132,6
1000-1100	3,0	1050	3150	135,6
1100-1200	3,0	1150	3450	138,6
1200-1300	1,7	1250	2125	140,3
1300-1400	1,8	1350	2430	142,1
Свыше 1400	6,1	1450	8845	148,2
Итого	148,2	–	76140	–

Определить:

1) среднедушевой месячный доход;

2) нижний и верхний децили;

3) децильный коэффициент дифференциации доходов населения.

Решение.

1. Среднедушевой месячный доход равен

2. Нижний и верхний децили исчисляют по формуле медианы. Только вместо медианного интервала используют интервалы, в которых находятся варианты, отсекающие по 10% численности частот в разных концах ряда распределения.

Нижний дециль (самые низкие доходы) определяются по формуле

. (1.14)

Для расчета первого (нижнего) дециля находим 1/10 численности частот:

По накопленным частотам видно, что вариант, соответствующий такой частоте, находится в интервале 100-200 руб., тогда

Отсюда самые низкие доходы равны:

Верхний дециль (самые высокие доходы) определяется по формуле:

. (1.15)

Для расчета девятого (верхнего) дециля находим численности частот:

.

По накопительным частотам видно, что вариант, соответствующие такой частоте и отсекающий численности частот, находится в интервале 1000-1100 руб., тогда Отсюда самые высокие доходы равны

3. Децильный коэффициент дифференциации доходов населения составляет

Децильный коэффициент дифференциации доходов населения показывает, что среднедушевой денежный доход, выше уровня которого имели доход 10% населения (высокодоходная группа), в анализируемом году превышал в 6,2 раза уровень дохода, ниже которого имели доход 10% населения (низкодоходная группа).

Пример 1.1.2. Имеются следующие данные о распределении общего объема денежных доходов населения региона по 20%-м группам, %

Таблица 1.2

Показатель	Базисный год	Отчетный год
Денежные доходы всего	100	100
в том числе по 20% группам населения
Первая (с наименьшими доходами)	9,8	6,54
Вторая	14,9	10,6
Третья	18,8	16,5
Четвертая	23,8	22,5
Пятая (с наибольшими доходами)	32,7	43,9

Для каждого года:

1) определить коэффициенты концентрации дохода Джини;

2) построить кривую Лоренца.

Решение.

1. Коэффициент Джини равен:

для базисного года

для отчетного года

Увеличение коэффициента Джини с 0,219 в базисном до 0,347 в отчетном году свидетельствуют об усилении дифференциации доходов населения региона.

Таблица 1.3

Год	Социальная группа населения	Доля населения	Доля в общем объеме денежных доходов	Расчетные показатели
				Cum
Базисный	1 2 3 4 5	0,2 0,2 0,2 0,2 0,2	0,098 0,149 0,188 0,238 0,327	0,098 0,247 0,435 0,675 1,0	0,0196 0,0298 0,0376 0,0476 0,0654	0,0196 0,0494 0,0870 0,1346 0,2000
	ИТОГО	1,0	1,0	–	0,2	0,4906
Отчетный	1 2 3 4 5	0,2 0,2 0,2 0,2 0,2	0,065 0,106 0,165 0,225 0,439	0,065 0,171 0,336 0,561 1,0	0,0130 0,0212 0,0330 0,045 0,0878	0,0130 0,0342 0,0672 0,1122 0,2000
	ИТОГО	1,0	1,0	–	0,2	0,4266

2. Строим кривую Лоренца для каждого года

Кривая Лоренца иллюстрирует усиление неравномерности в распределении общего объема денежных доходов в отчетном году по сравнению с базисным. Так, наиболее обеспеченна группа населения сконцентрировала в отчетном году 43,9% доходов против 32,7: в базисном, а доля наименее обеспеченной группы в общем доходе снизилась с 9,8 до 6,5%

Пример 1.1.3. По данным выборочного обследования бюджетов домашних хозяйств рассчитать коэффициенты эластичности потребления продуктов питания.

Таблица 1.4

Показатель	Год
	базисный	отчетный
Потребление в среднем на одного члена домохозяйства в год, кг: хлебопродуктов молока и молочных продуктов Среднедушевые доходы на домохозяйство за год в сопоставимых ценах, руб.	100 296 2400	106 274,7 2688

Решение. Рассчитаем коэффициент эластичности потребления продуктов от дохода по формуле

где Δy – изменение уровня потребления в отчетном периоде по сравнению с базисным, т.е. Δy = y₁ – y₀;

y₀,y₁ – уровни потребления соответственно в базисном и отчетном периодах;

Δx – изменение среднедушевого дохода за данный период, т.е.

Δx = x₁ – x₀;

x₀,x₁ – среднедушевой доход соответственно в базисном и отчетном периодах.

Представим расчетные показатели в следующем виде:

Таблица 1.5

Показатель	Абсолютный прирост	Темп роста, %	Темп прироста, %
Потребление в среднем на одного члена домохозяйства в год, кг:
хлебопродуктов	6	106	6
молока и молочных продуктов	-21,3	92,8	-7,2
Среднедушевые доходы на одно домохозяйство за год (в сопоставимых ценах), руб.	288	112	12

Коэффициент потребления хлебопродуктов равен эластичности

или К_эл = 6 / 12 = 0,5%.

Коэффициент эластичности потребления молока и молочных продуктов равен

или К_эл = -7,2 / 12 = -0,6%.

Следовательно, потребление хлебопродуктов составило 0,5% на 1% прироста доходов, а по молоку и молочным продуктам наблюдалось снижение потребления, равное 0,6% на 1% прироста доходов.