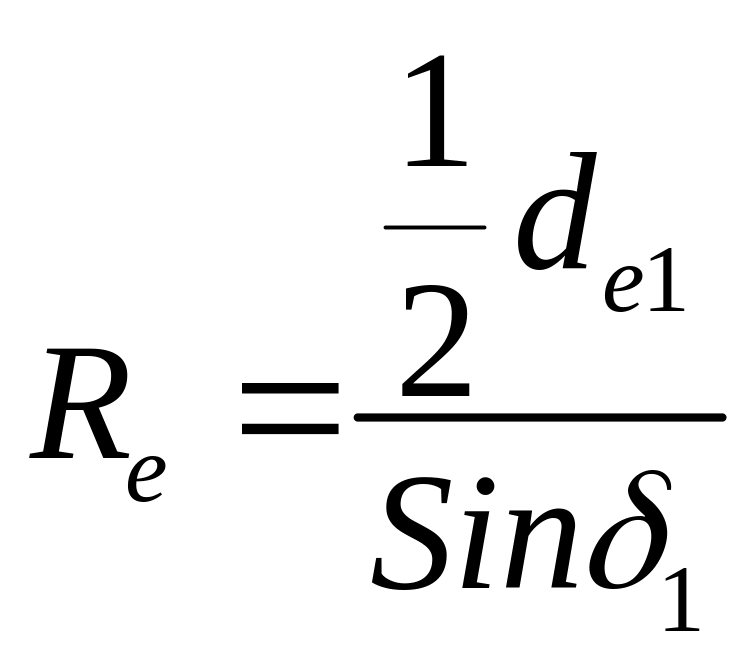2. Кинематический и силовой расчет

2.1 Определение передаточных отношений

Общее передаточное отношение привода

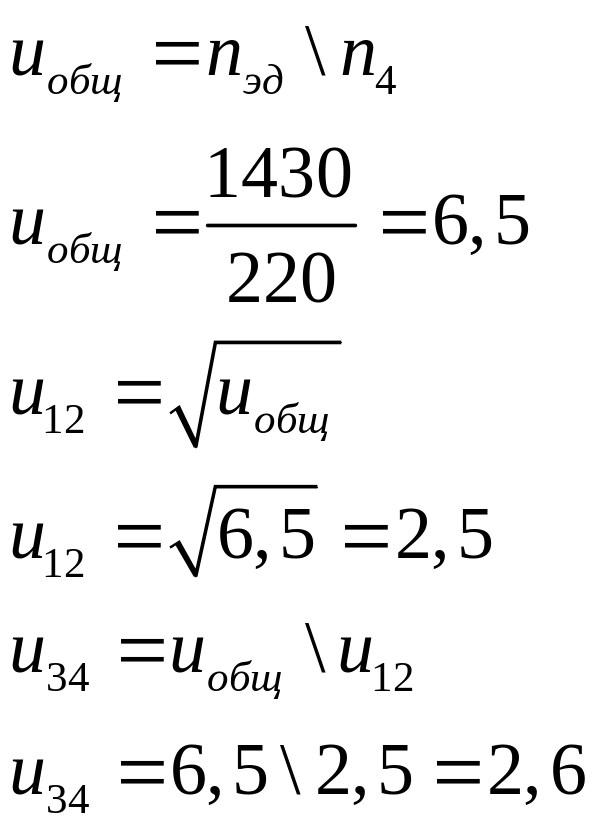
2.2 Определение частоты вращения валов

-частота вращения

2.3 Определение угловых скоростей

2.4 Мощности на валах

2.5 Моменты на валах

Таблица 2.1 Основные кинематические и силовые параметры привода

№ передачи	Передаточное отноше -ние	№ вала	Р, кВт	n,об/мин	, рад/с	Т, Н м
1-2	2,5	1	9,2	1430	149,67	61,47
		2-3	8,74	572	59,87	145,99
3-4	2,6
		4	8,22	220	23,03	356,99

3 . Расчет передачи привода

Рис 3.1 Эскиз передачи конической

3.1 Выбор материалов зубчатых колес

Так как к приводу не предъявляется особых требования по массе и габаритам, принимаем материалы со средними техническими характеристиками. С целью обеспечения равной прочности шестерни и колеса и уменьшения задира, твёрдость рабочих поверхностей зубьев шестерни должна быть примерно на 10% выше твёрдости рабочих поверхностей колеса.

Таблица 3.1 Выбор материалов, термообработки и твердости зубчатых колес

Звено	Материал	Твердость	Термообработка
Шестерня 3	Ст45	280	Улучшение
Колесо 4	Ст45	255	Улучшение

3.2 Расчёт допускаемых напряжений

3.2.1 Расчёт допускаемых контактных напряжений

_,

где S_H - коэффициент безопасности (S_H=1,1 т.к. материал с однородной структурой);

_{H lim}- предел контактной выносливости зубьев, соответствующий эквивалентному числу циклов перемены напряжений, Н/мм²;

,

где _{H lim в} - предел контактной выносливости поверхности зубьев, соответствующий базовому числу циклов перемены напряжений, Н/ мм²;

K_HL - коэффициент долговечности (K_HL = 1 , так как срок службы передачи неограниченно долгий).

I. Шестерня

.

II. Колесо

3.2.2 Определение допускаемых значений напряжений при расчёте зубьев на усталостный изгиб

_,

где _FlimB- предел выносливости при изгибе, соответствующий эквивалентному числу циклов нагружений;

S_F – коэффициент безопасности (S_F=1,7..2,2); принимаем S_F=1,75;

K_FL - коэффициент долговечности (K_FL = 1);

,

где – базовое число циклов перемены напряжений;

_,

1. Шестерня

=1,8∙ 280=504 МПа

, принимаем

1. Колесо

=1,8∙ 255=459 МПа

, принимаем

3.3 Определение коэффициентов нагрузки

3.3.1 Коэффициент концентрации нагрузки

Коэффициенты нагрузки находятся по следующим зависимостям:

- при расчёте на контактную выносливость: К_Н = К_Н К_НV;

- при расчёте на изгибную выносливость: К_F = К_FК_FV,

где К_Н,К_F - коэффициенты, учитывающие неравномерность распределения нагрузки по длине зуба при расчёте по контактным и изгибным напряжениям соответственно;

К_НV, К_FV – динамические коэффициенты при расчёте по контактным и изгибным напряжениям соответственно.

Рисунок 3.2 Схема расположения зубчатых колёс относительно опор.

Параметр выбираем по таблице 6.3 [2]. При расчете прямозубых конических колес при коэффициенте ширины зубчатого венца:

Значения динамических коэффициентов выбираем в зависимости от окружной скорости в зацеплении, точности изготовления передачи и твердости зуба.

Для вычисления приближенной окружной скорости воспользуемся формулой:

,

где - частота вращения шестерни рассчитываемой пары колёс,1/мин; - вспомогательный коэффициент.

по табл. 5.2 [2] принимаем 8-ю степень точности.

По графическим зависимостям и по заданной схеме закрепления зубчатых колёс находим значения коэффициентов:

Определяем коэффициенты К_НV и К_FV:

,

3.4 Передачи прямозубыми коническими колесами

3.4.1 Расчет передач прямозубыми коническими колесами по контактным напряжениям

Таблица 3.2 Исходные данные для расчета

Наименование	Обозначение	Величина и размерность
Крутящий момент на шестерне		145,99 Нм
Крутящий момент на колесе		356,99 Нм
Передаточное число пары		2,6
Частота вращения шестерни		572 об/мин

3.4.2 Определяем диаметр внешней делительной окружности колеса

Рисунок 3.3 Коническое зацепление

Полученное значение округляем до ближайшего большего по ГОСТ 12289-76 (таблица 2.2 [3]), создание которого объясняется достижением возможности централизованного изготовления заготовок. Таким образом, получаем .

3.4.3 Определение модуля зацепления на внешнем делительном диаметре

Необходимо знать число зубьев шестерни ( ) и колеса ( ). Зададим число зубьев шестерни .

Число зубьев колеса определяется расчётом: .

Полученное значение округляем до ближайшего целого: .

Тогда внешний окружной модуль будет равен:

3.4.4 Проверочный расчет по контактным напряжениям

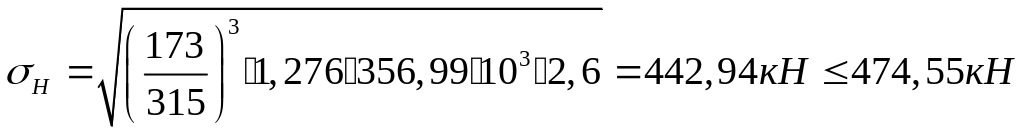
3.4.5 Определение основных размеров и сил в зацеплении

Таблица 3.3 Основные размеры и силы в зацеплении

Наименование	Формула	Подстановка и вычисление
Число зубьев шестерни		23
Число зубьев колеса		60
Модуль зацепления		5,25
Внешний делительный диаметр, мм
Углы делительных конусов
Внешнее конусное расстояние, мм
Длина зуба, мм
Среднее конусное расстояние, мм
Средний окружной модуль, мм
Средний делительный диаметр,мм
Внешняя высота головки зуба, мм
Внешняя высота ножки зуба, мм
Угол головки зуба
Угол ножки зуба
Внешний диаметр вершин, мм
Окружная сила, Н
Радиальная сила на колесе (осевая на шестерне),Н
Осевая сила на колесе (радиальная на шестерне)		Fa3=Fr4=2644,37•tg20•Cos69,04=888,98

3.4.6 Проверочный расчет по напряжениям изгиба

_,

где - коэффициент прочности зубьев, который выбирается (по таблице 6.4 [2]) в зависимости от эквивалентного числа зубьев:

Проверка проводится для шестерни и колеса отдельно.

Для колеса: Для шестерни:

;