4. Формирование маршрутов движения транспортных средств с помощью методов Свира и «ветвей и границ»

При использовании метода Свира следует учитывать, что количество пунктов включаемых в один маршрут должно быть не более пяти.

Метод Свира позволяет определить какие пункты включаются в развозочный маршрут, обслуживаемый одним автомобилем, и заключается в следующем:

- воображаемый луч, исходящий из точки, где расположен грузоотправитель, постепенно вращается по (или против) часовой стрелке, "стирая" с карты изображения грузополучателей. В тот момент, когда сумма заказов "стертых" грузополучателей достигнет вместимости транспортного средства, фиксируется сектор, обслуживаемый одним кольцевым маршрутом.

При решении студент должен определиться с маркой и моделью автотранспортных средств (одной или несколькими), которые будут использоваться на развозочных маршрутах. Выбор производиться самостоятельно в соответствии с собственным опытом, сведениями, приведенными в паспорте транспортного средства, или по данным справочной литературы, например [2].

Метод должен быть проиллюстрирован на схеме, построенной в первом задании. Обязательным является наглядное представление тех пунктов, которые будут включены в один маршрут, а так же выделение полученных секторов обслуживания.

Для полученных маршрутов требуется с использованием формулы (1) построить матрицу кратчайших расстояний между всеми пунктами.

Решение задачи коммивояжера, то есть определение оптимального порядка объезда пунктов развозочного маршрута, производиться методом «ветвей и границ», который состоит из следующих этапов:

• производится приведение матрицы кратчайших расстояний и определение нижней границы (x) для множества "все маршруты" (вершины дерева решений):

(5)

где h_i, h_j – константы приведения соответственно по строкам и столбцам.

h_i = min( l_ij), i = 1, 2, …, n; (6)

l_ij' = l_ij – h_i, i, j = 1, 2, …, n (7)

где l_ij' – элемент новой матрицы приведенной по строкам;

h_j = min (l_ij'), j = 1, 2, …, n; (8)

l_ij'' = l_ij' – h_j, I, j = 1, 2, …, n (9)

где l_ij'' – элемент новой матрицы после следующего приведения исходной матрицы по столбцам;

• определяются оценки Q_ij для клеток с нулевыми элементами l_ij = 0 в новой матрице L':

при условии: k  j; s  i; k, s = 1, 2, …, n,

где l'_ik – наименьшее значение элемента в строке i;

l''_sj – наименьшее значение элемента в столбце j.

• определяются пары (ks) с максимальной оценкой, то есть:

(10)

От начальной вершины "все решения" проводят ответвление вершин ks и с нижними границами:

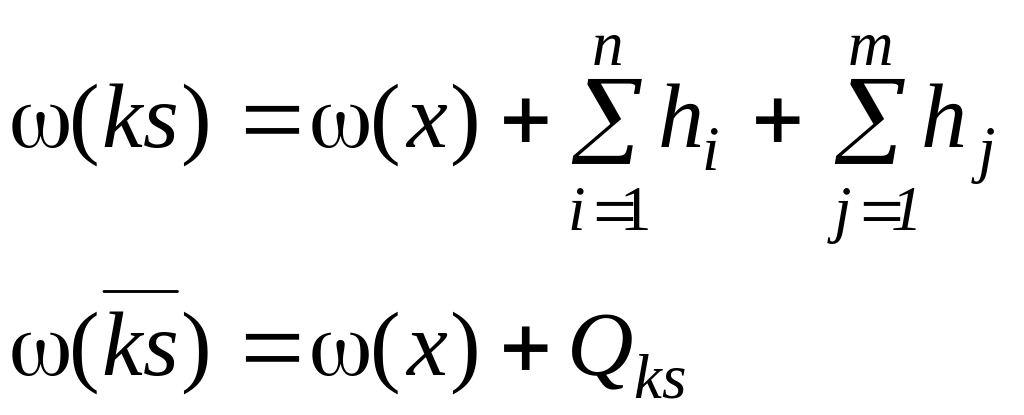(11)

где ks – маршруты подмножества, включающего пункты k и s;

- маршруты подмножества, не включающего пункты k и s.

• из матрицы исключаются строка k и столбец s. Элементу, находящемуся на пересечении строки s и столбца k, присваивается значение бесконечности ( ), то есть накладывается запрет на его включение в маршрут или блокирование.

• после блокировки операция приведения повторяется, но уже для новой матрицы L' с вычеркнутой строкой k и столбцом s и заблокированными необходимыми элементами l_ij. Для ветвления выбирают следующую вершину, имеющую наименьшую нижнюю границу, и так до получения матрицы размером два на два. В этой матрице пары, включенные в маршрут, определяются однозначно, и в результате формируется оптимальный развозочный маршрут.

Пробег с грузом (L_г), общий пробег (L_о) и транспортная работа (Р) для развозочных маршрутов определяются по следующим формулам:

(12)

(13)

(14)

где m – количество развозочных маршрутов;

t – количество пунктов на маршруте (пункт погрузки учитывается два раза);

– пробег между соседними пунктами маршрута, км;

- суммарный объем перевозок на m-ом маршруте, т;

q_s – объем груза, выгружаемый в s-ом пункте, т.

По результатам решения третьего и четвертого пунктов задания следует заполнить табл. 5, сделать количественные и качественные выводы.

Таблица 5

Сравнение технико-эксплутационных показателей

Показатель	Пробег с грузом, км	Общий пробег, км	Транспортная работа, ткм
после решения транспортной задачи
после решения задачи маршрутизации

Пример:

Предположим, что пункты закрепленные за грузоотправителем А образуют один маршрут, при этом условие о невозможности включения в один маршрут более пяти пунктов выполняется. Аналогичная ситуация наблюдается и у грузоотправителя Б. Таким образом, метод Свира предполагает использование автомобиля грузоподъемностью более 4,7 тонн на маршруте от грузоотправителя А и более 5,5 тонн – от грузоотправителя Б.

Пусть в рассматриваемом примере для обслуживания двух маршрутов привлекается одинаковый подвижной состав – ЗИЛ – 43311, грузоподъемность которого составляет 6 тонн.

Для грузоотправителя А построим матрицу кратчайших расстояний (табл. 6).

В каждой строке находим минимальный элемент h_i и выполним приведение матрицы по строкам, то есть определим значения l_ij' по формуле (7). Полученный результат представим в табл. 7.

Далее полученную в табл. 7 матрицу необходимо привести по столбцам по формулам (8) и (9). Результат приведения представлен в табл. 8.

Таблица 6

Матрица кратчайших расстояний для первого маршрута

(грузоотправитель А)

Пункты маршрута	А	2	6	8	9	10
А		8	8	7	10	10
2	8		5	1	18	1
6	8	5		5	15	6
8	7	1	5		17	3
9	10	18	15	17		19
10	10	1	6	3	19

Таблица 7

Матрица кратчайших расстояний, приведенная по строкам

Пункты маршрута	А	2	6	8	9	10	hi
А		1	1	0	3	3	7
2	7		4	0	17	0	1
6	3	0		0	10	1	5
8	6	0	4		16	2	1
9	0	8	5	7		9	10
10	9	0	5	2	18		1
Итого:							25

Таблица 8

Матрица кратчайших расстояний, приведенная по столбцам

Пункты маршрута	А	2	6	8	9	10	Итого:
А		1	0	0	0	3
2	7		3	0	14	0
6	3	0		0	7	1
8	6	0	3		13	2
9	0	8	4	7		9
10	9	0	4	2	15
hj	0	0	1	0	3	0	4

Нижняя граница, то есть минимально возможная длина маршрута, определяется по формуле (5) и равна:

= 25 + 4 = 29

Для нулевых элементов матрицы, приведенной в табл. 8, определим оценки Q_ij, которые проставим в правом нижнем углу соответствующей ячейки. Так для нулевого элемента, находящегося на пересечении строки А и столбца 6, оценка Q_А6 = 0 + 3 = 3 (минимальное значение по строке – 0, а по столбцу – 3). При этом необходимо помнить, что элемент, для которого производиться расчет, не учитывается и необходимо искать следующее наименьшее значение.

Результаты расчета оценок представлены в табл. 9.

Таблица 9

Расчет оценок для нулевых элементов

Пункты маршрута	А	2	6	8	9	10
А		1	0 3	0 0	0 7	3
2	7		3	0 0	14	0 1
6	3	0 0		0 0	7	1
8	6	0 2	3		13	2
9	0 7	8	4	7		9
10	9	0 2	4	2	15

В табл. 9 получили две максимальные оценки равные 7. Для дальнейшего решения выберем одну из них, какую не имеет принципиального значения. Пусть ветвь маршрута будет А-9. Таким образом, исключает из дальнейшего рассмотрения строку k = А и столбец s = 9. На пересечении девятой строки и столбца А ставим знак .

Проверяем условие, что бы в каждой строке и столбце усеченной матрицы были нулевые значения, оно не выполняется, поэтому операция приведения проводится заново. В строке 9 столбце А определяем h_i и h_j, вычитаем полученные значения из всех элементов строки и столбца (табл. 10).

От начальной вершины "все решения" проводят ответвление вершин ks и с нижними границами:

Графическое изображение полученного решения приведено на рис. 1.

Таблица 10

Приведение матрицы усеченной на строку А и столбец 9

Пункты маршрута	А	2	6	8	10	hi
2	4		3	0	0	0
6	0	0		0	1	0
8	3	0	3		2	0
9		4	0	3	5	4
10	6	0	4	2		0
hj	3	0	0	0	0	-

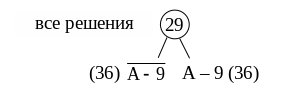
Рис. 1. Первое ветвление «дерева решений» для метода «ветвей и границ»

Далее производиться расчет оценок для нулевых значений усеченной матрицы, выбирается максимальное значение, которое покажет новое ветвление «дерева решений» (табл. 11).

Таблица 11

Определение оценок для усеченной матрицы

Пункты маршрута	А	2	6	8	10
2	4		3	0 0	0 1
6	0 3	0 0		0 0	1
8	3	0 2	3		2
9		4	0 6	3	5
10	6	0 2	4	2

В рассматриваемом случае наибольшим значением оценки является 6, которое расположено на пересечении строки девять и столбца шесть. Получаем две «ветки дерева решений» 9 – 6 и . Исключаем из дальнейшего рассмотрения указанные строку и столбец. Знак не проставляется, так как столбец девять уже был исключен при первой усечении матрицы кратчайших расстояний.

В матрице 4 х 4 в каждой строке и столбце находиться нулевой элемент, поэтому верхняя граница ветки 9 – 6 не увеличивается. Полученное ветвление отмечаем на «дереве решений» (рис. 2).

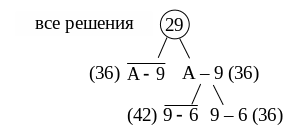
Рис. 2. Второе ветвление «дерева решений»

Следующее усечение матрицы представлено в табл. 12.

Таблица 12

Определение оценок для матрицы 4 х 4

Пункты маршрута	А	2	8	10
2	4		0 0	0 1
6	0 3	0 0	0 0	1
8	3	0 2		2
10	6	0 2	2

Наибольшее искомое значение получаем для элемента, расположенного на пересечении строки шесть и столбца А.

Однако, в данном случае выбор указанной ветки не может быть произведен, так как тогда маршрут замкнется и не будет включать все пункты, а именно второй, восьмой и десятый. Таким образом, требуется принудительно поставить знак в рассмотренную ячейку и увеличить нижнюю границу на величину оценки , а «дерево решений» дополниться новым ветвлением (рис. 3). В табл. 12 требуется пересчитать элементы, получив в столбце А нулевое значение, и далее определить новые оценки. Результат приведен в табл. 13.

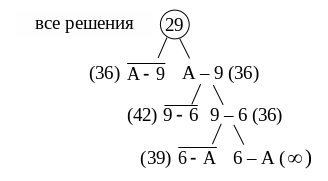
Рис. 3. «Дерево решений», не включающее ветку 6 - А

Таблица 13

Определение оценок для матрицы четыре на четыре после принудительного исключения элемента 6 - А

Пункты маршрута	А	2	8	10
2	1		0 0	0 1
6		0 0	0 0	1
8	0 1	0 0		2
10	3	0 2	2

Наибольшее значение на пересечении строки десять и столбца два. Проводя расчеты аналогичным образом, получаем матрицу 2 х 2, в которой однозначно представлены две последние «ветки» маршрута (табл. 14).

Таблица 14

Матрица 2 х 2 для метода «ветвей и границ»

Пункты маршрута	8	10
2	0
6	0 0	0

При этом «дерево решений» примет окончательный вид, который проиллюстрирован на рис. 4.

Анализируя полученные участки (ветви), имеем следующий маршрут: А 9 6 10 2 8 А, длина которого составляет 40 км.

Рис. 4. «Дерево решений» для грузоотправителя А

Проверим, правильно ли была определена нижняя граница, для чего просуммируем соответствующие расстояния между пунктами маршрута, приведенные в табл. 5: 10 + 15 + 6 + 1 + 1+ 1+ 7 = 40 км.

Проводя расчеты аналогичным образом для грузоотправителя Б, получаем маршрут: Б 1 3 7 5 4 Б, длиной 29 км.

Определяя значения технико-эксплутационных показателей по формулам (12) – (14), получаем: L_г = 52 км; L_о = 69 км; Р = 195 ткм.