§7. Ряд Фурье.
Определение:
Тригонометрический
ряд —
(1)
Числа
называются коэффициентами
тригонометрического
ряда.
Если
тригонометрический ряд сходится, то на
интервале сходимости он также является
-периодической
функцией. Если тригонометрический ряд
равномерно сходится на отрезке
,
то в силу периодичности он также сходится
на любом отрезке числовой оси, и его
сумма
является непрерывной функцией во всех
точках интервала сходимости.
ТЕОРЕМА 1. Пусть — -периодическая, непрерывная на или имеющая конечное число точек разрыва I рода функция. Тогда разложение в тригонометрический ряд существует, и его коэффициенты равны:
(2)
(3)
Определение.
Коэффициенты
и
,
которые определяются по формуле (1),
называются
коэффициентами Фурье
для функции
.
Определение. Ряд Фурье для функции — это тригонометрический ряд, коэффициенты которого являются коэффициентами Фурье для функции .
Если ряд Фурье для функции сходится к во всех точках её непрерывности, то говорят, что разлагается в ряд Фурье.
Достаточные условия разложимости в ряд фурье
Определение.
Пусть
монотонна на каждом из промежутков, на
который разбивается отрезок
,
и этих промежутков конечное число. Тогда
называется кусочно-монотонной
на
.
ТЕОРЕМА 2 (теорема Дирихле). Пусть -периодическая, кусочно-монотонная и кусочно-непрерывная на , причём имеет точки разрыва только I рода. Тогда:
1.
Ряд Фурье функции
сходится при всех значениях x,
причём в точках непрерывности его сумма
равна
,
а в точках разрыва
.
2. Ряд Фурье функции равномерно сходится на любом отрезке, лежащем внутри интервала непрерывности функции .
Определение.
называется кусочно-гладкой
на
,
если
и
непрерывны на
,
или имеют конечное число разрывов I
рода.
ТЕОРЕМА 3. Пусть -периодическая, кусочно-гладкая на . Тогда имеют место утверждения (1) и (2) предыдущей теоремы.
Разложение в ряд Фурье чётных и нечётных функций
Для
чётной
-периодической
функции
коэффициенты разложения в ряд Фурье:
(1)
,
,
Аналогично, для нечётной -периодической функции коэффициенты Фурье:
(2)
,
,
Собственно
разложение: (3)
,
— чётная,
-периодическая
функция,
из (1).
(4)
,
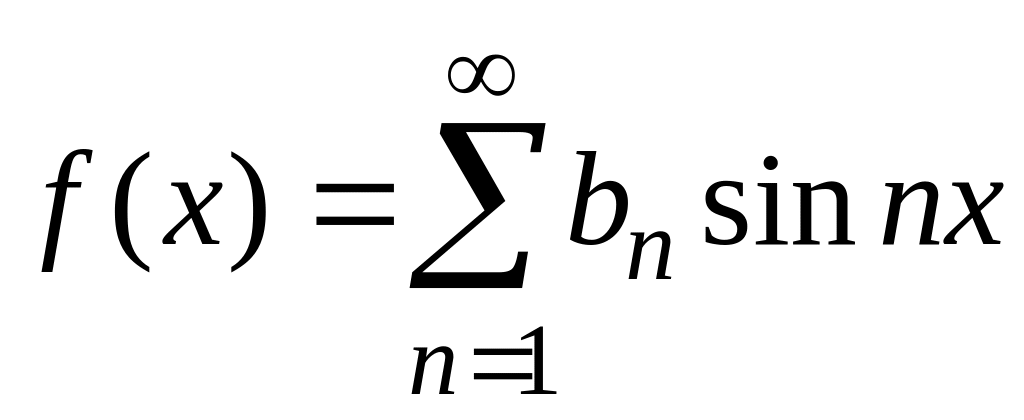— нечётная,
-периодическая
функция,
определять по (2).
Пример
1: Функция
—
-периодическая
и на
.
Разложить в ряд Фурье.
Достаточно
получить разложение на отрезке
и продолжить на всю ось как периодическую
функцию.
— нечётная, поэтому разложение находим
по формуле (4), коэффициенты найдём по
формуле (2).
Коэффициенты Фурье находятся по формуле:
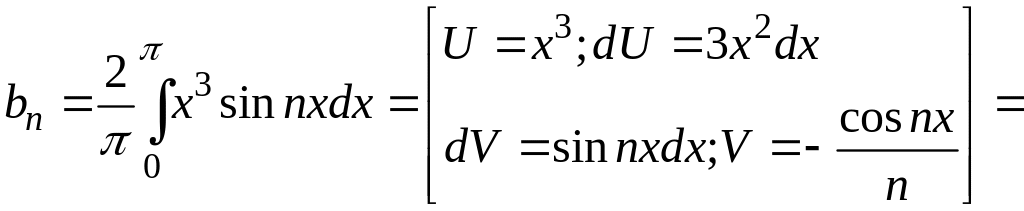
Разложение в ряд Фурье функции с произвольным периодом.
Пусть
— периодическая с периодом
,
на отрезке длины
непрерывна или имеет конечное число
точек разрыва 1-го рода.
Тогда ряд Фурье имеет вид:
;
;
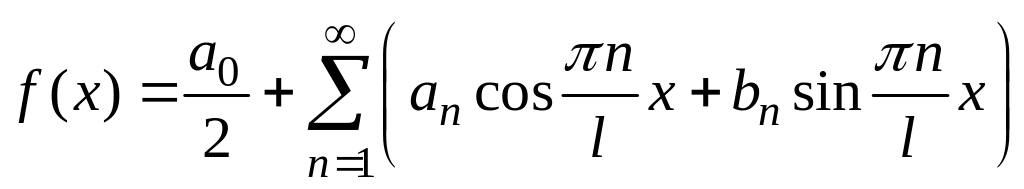
Для чётной функции произвольного периода разложение в ряд Фурье:
Для нечётной функции с периодом :
