
- •Эталонные ряды
- •§3. Знакопеременные ряды. Абсолютная и условная сходимости. Знакочередующиеся ряды. Признак Лейбница.
- •§4 Функциональные ряды.
- •§5 Степенные ряды.
- •Свойства степенных рядов.
- •Формула Тейлора.
- •3. Разложение в ряд Маклорена основных элементарных функций.
- •§7. Ряд Фурье.
- •Достаточные условия разложимости в ряд фурье
- •Разложение в ряд Фурье чётных и нечётных функций
- •Разложение в ряд Фурье функции с произвольным периодом.
- •Разложения в ряд Фурье непериодической функции.
- •Ряд Фурье по ортогональной системе функций
- •Ряд Фурье по ортогональной системе функций
Свойства степенных рядов.
Следствие 1: Сумма степенного ряда является непрерывной функцией на всём интервале его сходимости.
Замечание: на отрезке сумма степенного ряда может быть разрывной.
Пример
3: геометрический
ряд
 сходится на интервале
и его сумма
сходится на интервале
и его сумма
![]() непрерывна на этом интервал, но имеет
разрыв на правом конце
непрерывна на этом интервал, но имеет
разрыв на правом конце
Следствие 2: степенной ряд (1) можно почленно дифференцировать в интервале сходимости; при этом ряд, составленный из производных:
также является степенным;
имеет тот же радиус сходимости;
имеет сумму равную производной суммы исходного ряда (в каждой точке интервала сходимости). (без доказательства)
Следствие
3: степенной
ряд можно почленно интегрировать на
отрезке
![]() с
;
полученный ряд имеет вид
с
;
полученный ряд имеет вид
 и имеет тот же радиус сходимости.
и имеет тот же радиус сходимости.
Формула Тейлора.
Определение.
Пусть
![]() дифференцируема до порядка
дифференцируема до порядка
![]() включительно в некоторой окрестности
точки
включительно в некоторой окрестности
точки
![]() .
Тогда
многочлен Тейлора
.
Тогда
многочлен Тейлора![]() или
или
![]() определяется по формуле
определяется по формуле
 (1)
(1)
и зависит от функции , , точки .
Определение.
Величину
![]() (2) назовём
остаточным
членом
формулы Тейлора (остатком).
(2) назовём
остаточным
членом
формулы Тейлора (остатком).
Свойства
остаточного члена: 1)
![]() .
2)
.
2)
![]() ,
при
,
при
![]() .
.
3)
Пусть
![]() в окрестности точки
.
Тогда
в окрестности точки
.
Тогда
![]() .
.
ТЕОРЕМА 1 (Формула Тейлора с остаточным членом в форме Пеано).
Пусть функция имеет в точке все производные до порядка включительно.
Тогда в некоторой окрестности точки имеет место представление:
 Доказательство:
Вычислим,
последовательно применяя правило
Лопиталя:
Доказательство:
Вычислим,
последовательно применяя правило
Лопиталя:
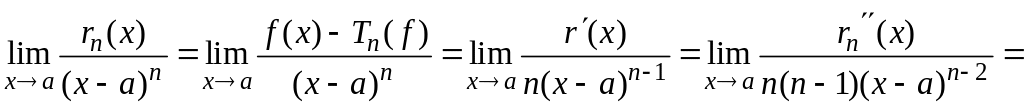
 .
.
ТЕОРЕМА 2 (Формула Тейлора с остаточным членом в форме Лагранжа):
Пусть
функция
имеет все производные до порядка
включительно на конечном отрезке
![]() .
Тогда
.
Тогда
![]() :
:

 .
(3)
.
(3)
Ряды Тейлора и Маклорена.
Пусть
степенной ряд
 (4)
имеет радиус
сходимости
.
Тогда на
ряд (4) сходится к
(сумме ряда).
(4)
имеет радиус
сходимости
.
Тогда на
ряд (4) сходится к
(сумме ряда).
 (6)
(6)
Определение: Ряд (4), где коэффициенты определяются по формуле (6) называются рядом Тейлора функции в определённой точке .
 .
.
Определение:
При
![]() ряд Тейлора называется рядом
Маклорена.
ряд Тейлора называется рядом
Маклорена.
Степенной ряд (4) является рядом Тейлора для своей суммы на интервале сходимости.
Определение:
функция
называется разложимой
в ряд Тейлора
в окрестности точки
,
если её ряд Тейлора сходится к
![]() ,
где
— радиус сходимости ряда Тейлора.
,
где
— радиус сходимости ряда Тейлора.
ТЕОРЕМА
3: (Необходимое
и достаточное условие). Функция
![]() разложима
в ряд Тейлора на множестве
разложима
в ряд Тейлора на множестве
![]() если и только если
если и только если
![]() для всех
для всех
![]() .
.
3. Разложение в ряд Маклорена основных элементарных функций.
1)
![]() (1)
(1)
2)
 (2)
(2)
3)
 (3)
(3)
4)
 (4)
(4)
5)
 (5)
(5)
6)
![]() (6)
(6)
7)
![]()
