
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
99 9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
Уп1 |
Уп2 |
II |
Уп3 |
Уп4 |
ТК Уп4 |
Уп5 |
Уп6 |
Уп7 |
Уп8 |
Уп10 |
Уп11 |
Уп12 |
Уп13 |
Уп14 |
Уп15 |
Уп16 |
Уп18 |
|
|
|
|
|
|
|
|
|
Уп9 |
II |
П |
II |
IV |
IV |
IV |
Уп17 |
Уп19 |
Рт, 1 курс, 2011/12 уч. год, Пушкарева Надежда Борисовна
Лабораторные работы:
Лаб. II № 4,7, 8,9 (можно 10 вместо 7)
Лаб. IV № 16, 18(а, б), 28
Программа
Валишев М.Г., Повзнер А.А., Курс общей физики
Дополнительный учебник: Трофимова Т.И « Курс физики»
Чертов А.Г., Воробьев А.А., Задачник по физике, 1988
Упр 1. Элементы кинематики материальной точки и вращательного движения абсолютно твердого тела.
Определения
кинематики: система отсчета, радиус-вектор
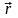 ,
скорость
,
скорость
 ,
ускорение
,
ускорение
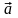 и его составляющие тангенциальное
и его составляющие тангенциальное
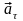 и
нормальное
и
нормальное
 ускорение при криволинейном движении
материальной точки. Связь нормального
ускорения со скоростью и радиусом
кривизны траектории.
ускорение при криволинейном движении
материальной точки. Связь нормального
ускорения со скоростью и радиусом
кривизны траектории.
Кинематика
вращения твердого тела вокруг неподвижной
оси. Угловая скорость
 и угловое ускорение
и угловое ускорение
 .
Связь между угловыми и линейными
кинематическими величинами.
.
Связь между угловыми и линейными
кинематическими величинами.
Задачи (Чертов) В классе 1. 3, 6,16 ,18, 21, 29, 36, 48, 53
Дома 1.5, 9,10, 14, 22, 34, 49, 54 - 57
Упр 2. Динамика материальной точки и поступательного движения твердого тела
Первый закон Ньютона, масса, сила. Второй закон Ньютона (уравнение движения). Силы в механике: сила упругости, сила трения, гравитационная сила и её составляющая сила тяжести. Третий закон Ньютона. Закон сохранения импульса для системы материальных точек как следствие законов Ньютона.
Задачи: В классе 2.3, 7, 12, 18, 36, 38, 44, 47
Дома 2.5, 10, 19, 22, 37,39, 46, 50
Упр 3. Работа и энергия. Определение элементарной и полной работы. Кинетическая энергия. Потенциальная энергия поднятого и упруго деформированного тела. Консервативные силы и системы, связь консервативной силы с потенциальной энергией. Закон сохранения механической энергии как следствие законов Ньютона. Графическое представление энергии, потенциальные кривые (потенциальная яма и потенциальный барьер). Задачи об абсолютно упругом и неупругом ударах.
Задачи: 2.58, 72, 73, 76, 78, 83, 86
Дома 2. 62, 75, 77, 79, 84, 87, 91
Упр 4. Механика твердого тела (динамика вращения твердого тела вокруг неподвижной оси)
Момент силы. Момент импульса. Закон сохранения момента импульса в замкнутой системе. Момент инерции. Моменты инерции кольца (полого цилиндра), диска (сплошного цилиндра), шара, стержня. Теорема Штейнера. Основное уравнение динамики вращательного движения (второй закон динамики). Работа сил, вращающих тело. Кинетическая энергия вращающегося и катящегося тел.
Задачи: 3.2, 12, 22, 27, 33, 35, 40, 41, 44, 51
Дома 3. 3, 15, 23, 26, 34, 36 , 45, 49, 50, 52
Упр 5. Теоретический коллоквиум по теме «Физические основы механики» (по материалам Упр.1 - Упр. 4) два теор. Вопроса + задача. При сдаче на 4 и 5 материал снимается с экзамена. или 1 теор+2 задачи
Упр 6. Теория относительности. Пространство и время в классической физике. Преобразования Галилея. Постулаты частной теории относительности. Событие. Относительность понятий одноместности и одновременности событий. Преобразования Лоренца. Следствие преобразований Лоренца: сокращение длин, замедление времени, релятивистская формула сложения скоростей. Парадокс мюона. Динамика частной теории относительности: масса, импульс, закон движения, кинетическая энергия, полная энергия (E = mc2 ). Связь энергии и импульса. Инварианты теории относительности.
В классе: 1)два стержня одинаковой собственной длины l0 движутся в продольном направлении навстречу друг другу параллельно общей оси с одной и той же скоростью v относительно лабораторной СО. Чему равна длина каждого стержня в Со, связанной с другим стержнем?
Задачи: 5.1, 5, 8, 15, 26,29, 31, 32, Дома 5.3, 7, 17, 24 , тест «СТО»-выполняется письменно, дома
Упр.7 Распределение Максвелла и Больцмана
Функция распределения. Распределение молекул по модулю скорости теплового движения в равновесном состоянии (функция Максвелла). Наиболее вероятная, среднеарифметическая и среднеквадратическая скорости молекул. Распределение молекул в поле силы тяжести (барометрическая формула). Распределение Больцмана. Степени свободы газовых молекул и принцип равнораспределения энергии теплового движения по степеням свободы. Энергия теплового движения в газе одно-, двух- и многоатомных молекул.
Задача 1. Определить температуру газообразного азота, при которой скоростям молекул 300 м/с и 600 м/с соответствуют одинаковые функции распределения.
Задача 2. Найти скорость газообразного азота. При которой значение f(v) для температуры Т0 будет такой же , как и для температуры в n раз большей.
Задачи:В классе 9. 28, 10.17, 19, 26, 4, 9
Дома 10. 4, 16, 18, 20, 28, 40, 5-7
Упр.8 Первое начало термодинамики
Количество теплоты и работа как величины, характеризующие процесс обмена энергией между системой и окружением. Внутренняя энергия. Первое начало термодинамики. Теплоемкость газов. Процессы в газах – изохорический, изобарический, изотермический и адиабатический (уравнение, работа, запись первого начала, характерные графики, теплоемкость).
Задачи: В классе 11. 4, 16, 32, 35, 48, 57
Дома 11. 6(см пример 1), 17, 33, 36, 50, 56, 58
Упр. 9 Второе начало термодинамики. Энтропия. Тепловые машины
Равновесные и неравновесные самопроизвольные процессы. Микро и макро распределение. Термодинамическая вероятность. Энтропия и её свойства. Энтропия и информация. Связь изменения энтропии с количеством подведенной теплоты. Изменение энтропии в изопроцессах. Второе начало термодинамики. КПД идеальной тепловой машины.
Задачи: 11.70 - 75, 61, 63, 64, 65.
Электромагнетизм
Упр. 10. Закон Кулона. Теорема Гаусса. Расчет полей. Закон Кулона. Электростатическое поле. Напряженность. Поток вектора напряженности. Теорема Гаусса. Применение теоремы Гаусса для расчета поля равномерно заряженной плоскости, непроводящего шара, равномерно заряженных нити, цилиндра, пластины.
В классе 13.2; 14.9, 7, 11, 14, 23, 28
Дома 13. 3, 4, 8, 13, 18, 20; 14. 3, 4, 10, 12, 16, 15, 25, 29, 36 или 38, 43
Тонкое проводящее кольцо радиуса R заряжено с линейной плотностью = 0cos,
где 0 = const, - азимутальный угол. Найти модуль напряженности электрического поля в центре кольца.
Упр. 11. Потенциал. Связь Е и потенциала. Работа по перемещению заряда
Потенциал. Связь напряженности и потенциала. Потенциальный характер электростатического поля, теорема о циркуляции вектора напряженности.
В классе 15. 5, 15, 22, 23, 31, 47, 56 Дома 15. 6, 14, 16, 24, 28, 45, 49, 58, 61
Упр. 12. Электроемкость. Конденсаторы. Энергия электрического поля
Проводники в электрическом поле. Напряженность поля вблизи поверхности заряженного проводника. Электроемкость. Конденсаторы. Электроемкость плоского, цилиндрического и сферического конденсаторов. Энергия заряженного конденсатора. Плотность энергии электростатического поля.
В классе: 17. 4, 5, 12, 16 18. 4, 5., 16, 18 Напомнить: раздвигают пластины конденсатора, как меняются q, U , C , если конденсатор отключен или подключен к источнику ; две заряженные сферы соединяют проволочкой, найти заряды и потенциал после соединения (см. абитурский задачник)
Упр.13 Постоянный ток. Законы Кирхгофа
В классе 19.3, 13, 15, 19, 30, 34, 36
Дома 19.14, 16, 20, 28, 29, 35
Упр. 14. Контрольная «Электростатика+постоянный ток» или Тест “Электростатика-2» (6 вопросов) на 45 мин + «Применение теоремы Гаусса к расчету полей…» и законы Кирхгофа
Упр.15 Расчет МП , Закон Био – Саварра – Лапласа. Теорема о циркуляции В
Задачи: В классе 21. 18, 22, 26, 27, 31 (а, б, в), обсудить индукцию «толстого» проводника с током (см. пример на лекции)
Дома 21. 6, 8, 10, 14, 19, 20, 21, 24, 31 (г, д, е)
Выдать на дом ИДЗ « Расчет магнитных полей» . Срок выполнения – 1 неделя
х
а


 В
классе 24. 9; 25. 13, 18, 11, 22(можно устно) , 17,
23,
В
классе 24. 9; 25. 13, 18, 11, 22(можно устно) , 17,
23,
I
26. 3
Дома: 24.10, 22. 3, 25; 25. 22, 29, 30, 31,36, 37,38,
40, 46, 43- 45, 22 26.4
v
прямой проводник с током I находятся в одной
I
с постоянной скоростью v. Найти Э.Д.С. индукции в
рамке как функцию расстояния х.
Ответ: Е=(μ0/2π)Ia2v/x(x+a)
Задача 2. П-образный проводник находится в перпендикулярном магнитном поле, меняющемся по закону В=0.1t . Вдоль параллельных сторон этого проводника перемещают проводник-перемычку с ускорением а=0.1 м/ с2. Длина перемычки b=0.2 м. Найти ЭДС индукции в контуре через 0.2 с после начала движения, если в начальный момент площадь контура и индукция магнитного поля были равны нулю. Индуктивностью контура пренебречь.
а
I
провода и квадратной рамки со стороной а. Расстояние
 между
рамкой и проводом равно а.
между
рамкой и проводом равно а.
Упр. 16.А (если будет время): (Сила Ампера и Лоренца):
Дома 22. 6, 9, 17, 27 ; 23. 8, 11, 16, 22(или 23, или 24), 30, 36, 39
25.7, 16, 18, 22, 24 :
Упр. 17 Уравнения Максвелла. Ток смещения. Бетатрон.
Задача 1. Чертов 25. 47
Задача 2. Найти отношение амплитудных значений плотности тока смещения и проводимости в диэлектрике, у которого удельное сопротивление ρ=1012 Ом*м, ε=10. Колебания электрического поля в диэлектрике происходят по закону Е=Еm cos(ωt), где ω=107 рад/ с.
Задача 3. Две заряженные проводящие плоскости радиусом R имеют поверхностные плотности |σ1|=| σ2|. Их замкнули накоротко. Считая, что в первый момент времени разрядный ток будет постоянным (Iпр=const), найти индукцию магнитного поля В, возникающую в первые моменты.
Задача 4. Площадь пластин конденсатора S=60 см2, первоначальное расстояние между ними d0=10 мм. Пластины конденсатора стали раздвигать со скоростью v=3 мм/ мин. Начальный заряд конденсатора q0=1 нКл. Определить модуль плотности тока смещения через 20 с после начала раздвижения, если:
1. Конденсатор отключен от источника напряжения;
2. Разность потенциалов между обкладками остается постоянной.
Задача 5. Плотность тока смещения в некоторой точке диэлектрика с диэлектрической проницаемостью ε меняется со временем по закону j cм =0.002 cos(104t) А/м2. По какому закону меняется напряженность электрического поля Е(t) .
Задача 6. (ИР. 3.366) Длинный прямой соленоид имеет n витков на единицу длины. По нему течет переменный ток I=Im sin(ωt). Найти плотность тока смещения как функцию расстояния r от оси соленоида. Радиус сечения соленоида R,
Задача 7. (ИР.3.365) Пространство между обкладками плоского конденсатора, имеющего форму круглых дисков, заполнено однородной слабо проводящей средой с удельной проводимостью σ и диэлектрической проницаемостью ε. Расстояние между обкладками d. Пренебрегая краевыми эффектами, найти напряженность магнитного поля между обкладками на расстоянии r от их оси, если на конденсатор подано переменное напряжение U=Um cos(ωt).
Дома 25. 48, 49
