8. Властивості параболи.

1. Парабола має вісь симетрії.

Змінна у входить у рівняння тільки у другому степені. Тому, якщо координати точки задовольняють рівняння параболи, то й координати точки задовольнятимуть його. Точка симетрична точці відносно осі Ох. Отже, вісь Ох є симетрією параболи. Вісь симетрії параболи називається віссю параболи. Точка перетину параболи з віссю називається вершиною параболи. Вершина параболи знаходиться в початку координат.

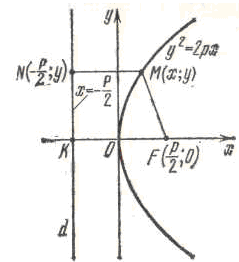
2. Парабола розміщена у півплощині х≥0.

Оскільки, параметр р додатний, то рівняння параболи можуть задовольняти тільки точки з невід’ємними абсцисами, тобто точки півплощини х≥0.

3. Парабола є об’єднанням графіків функцій .

9. Паралельний перенос параболи.

Використавши формули перетворення прямокутних координат при паралельному переносі отримаємо рівняння параболи зі зміщеною вершиною, .