5. Построение отклика системы на заданные входные воздействия
Заданы следующие входные воздействия и начальные условия:
U(t) = sin(t) t <= 6
U(t) = 0 t > 6
Y(0)=1
Y’(0)=0,1
Y’’(0)=0,2
Y’’’(0)=0
Следовательно, U(s) = 1/(1 + s2).
При нулевых начальных условиях:
-17s^2 -17s -17
y(s) = ——————————————————
( 0,1s^4 +15,1s^3 +8,4s^2 +104s +23)(s^2 +1)
При ненулевых начальных условиях отклик
системы порядка n
на непрерывное, дифференцируемое
входное воздействие u(t):
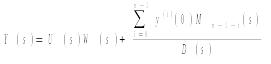
содержит
второе слагаемое, которое учитывает
продолжение движения в системе, имевшее
место при
т.е. до подачи
.
Здесь обозначено:
- полином степени
переменной
с коэффициентами
из набора коэффициентов характеристического
полинома
-ой
степени системы
;
,
D(s) = 0,1s^4 +15,1s^3 +8,4s^2 +104s +23
Следовательно,
Получили:
0,1s^5 +15,11s^4 +10,03s^3 +106s^2 -7,07s +90,86
Y(s) = —————————————————————
(s^2 +1)( 0,1s^4 +15,1s^3 +8,4s^2 +104s +23)
Входное воздействие U(s) является кусочно-непрерывным. Следовательно, представим отклик системы в виде:
Построим график y(t) на этих двух участках.
1.
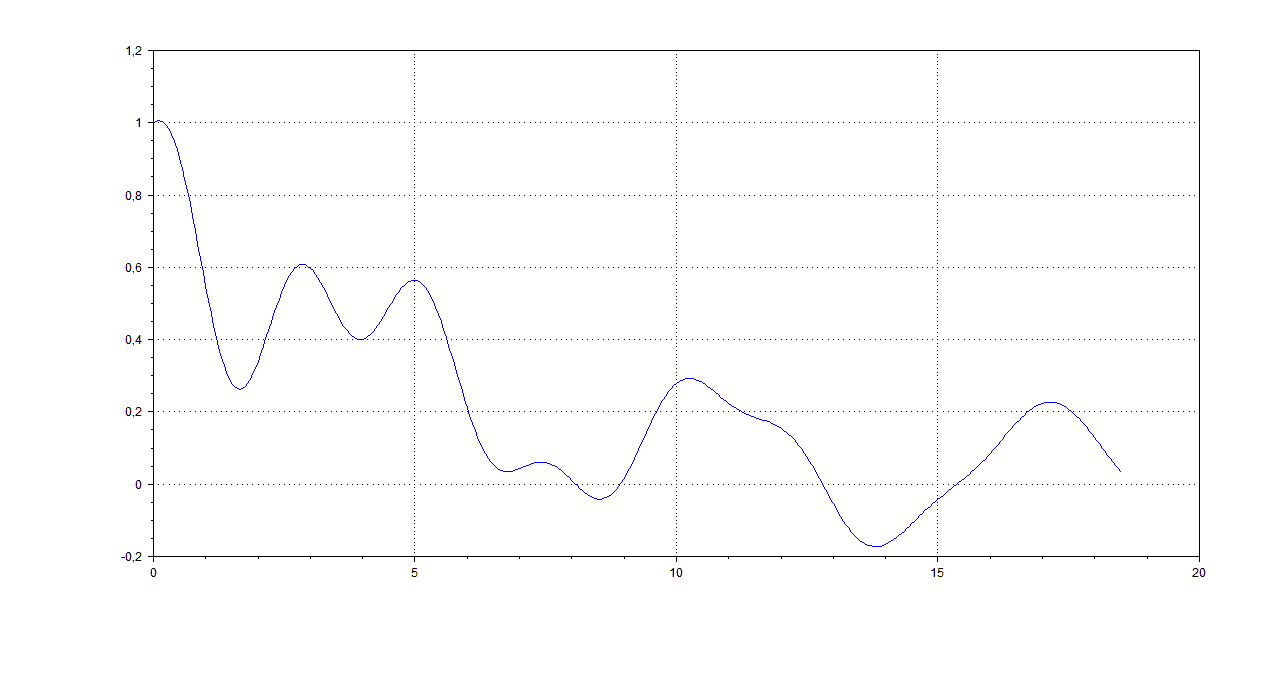
2.
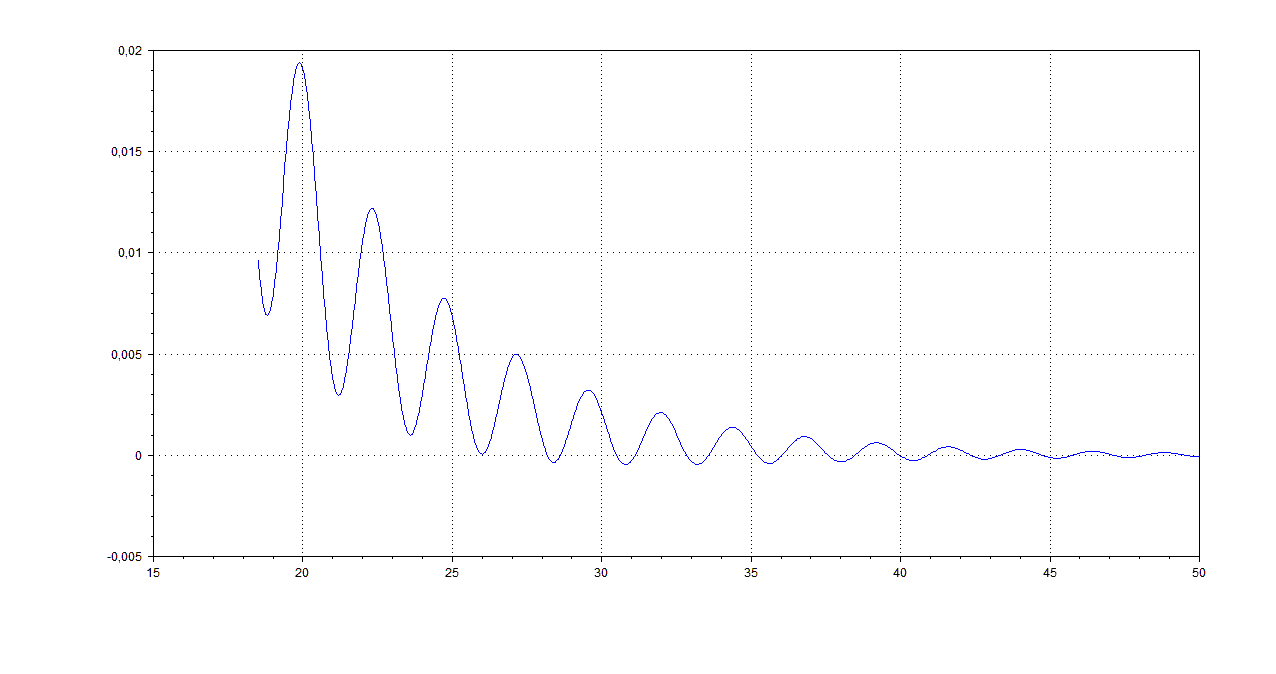
Выводы
В результате выполнения работы был построен корневой годограф системы и подобрано такое значение параметра par1, при котором выполняется. Аналогичный результат был достигнут введением в систему отрицательной обратной связи с первого выхода на первый вход. При этом порядок системы, а также свойство физической реализуемости, сохранились.
Далее, для следящей системы были установлены типовые ошибки, возникающие в ответ на типовые входные воздействия. Система оказалась статической первого порядка.
Далее в ходе работы путем варьирования параметров системы удалось свести к минимуму время переходного процесса. При этом, перерегулирование в системе отсутствовало.
И, наконец, были построены отклики стабилизированной системы на заданные входные воздействия.