
- •Основные понятия теории игр
- •Классификация игр
- •Описание игры в развернутой форме
- •Бескоалиционные игры
- •Приемлемые ситуации и ситуации равновесия в игре
- •Стратегическая эквивалентность игр
- •Антагонистические игры. Общие сведения
- •Чистые и смешанные стратегии
- •Верхняя и нижняя цены игры при использовании смешанных стратегий
- •Основная теорема антагонистических игр.
- •Верхние и нижние цены в s-игре
- •Теорема о минимаксе
- •Геометрическая интерпретация минимакса
- •Решение антагонистических игр. Доминирующие и полезные стратегии
- •Игры с частными случаями платежных матриц
- •Решение матричных игр
- •Линейное программирование для решения матричных игр
- •Графическое решение игр 2*n и m*2
- •Бесконечные антагонистические игры
- •Строго выпуклые игры на единичном квадрате
- •Неантагонистические игры
- •Бескоалиционные игры
Геометрическая интерпретация минимакса
Покажем, что точка , определяющая минимаксную стратегию второго игрока, является граничной точкой области , причем такой, в которой область T касается области .
![]() ,
причем
,
причем
![]() .
С другой стороны
.
С другой стороны
![]() ,
если
,
если
![]() ,
это множество m-мерных
векторов, каждая из координат которых
не превышает верхней цены игры.
,
это множество m-мерных
векторов, каждая из координат которых
не превышает верхней цены игры.
Рассмотрим точку
![]() ,
которая связана с точкой
следующим образом:
,
которая связана с точкой
следующим образом:
![]() ,
,
![]() ,
,
![]() ,
.
,
.
Очевидно, что
![]() ,
поэтому
,
поэтому
![]() ,
.
Значит,
,
.
Значит,
![]() .
Но
.
Но
![]() .
.
Из этого следует два вывода:
точка — граничная точка области ;
— точка, в которой область T касается области .
Эти свойства
позволяют легко находить геометрически
минимаксную стратегию
для случая, когда первый игрок имеет
две чистые стратегии, т.е. когда
эквивалентная S-игра
изображается множеством точек плоскости.
Для построения области T,
касательной к области
,
удобно провести вспомогательную прямую
из начала координат под углом
![]() к оси абсцисс, на которой лежит вершина
прямоугольного клина, образующего
область T.
к оси абсцисс, на которой лежит вершина
прямоугольного клина, образующего
область T.
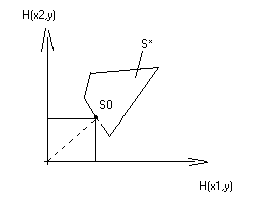
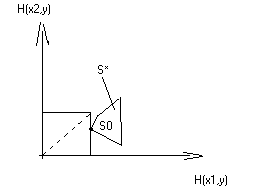
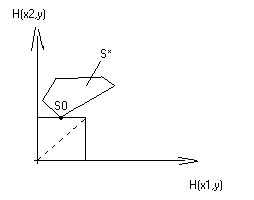
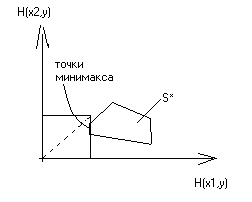
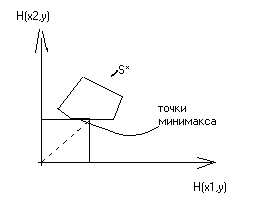
На рисунке приведены различные случаи взаимного расположения областей и T и отмечены точки, определяющие минимаксную стратегию второго игрока , и множества минимаксных стратегий второго игрока.
Решение антагонистических игр. Доминирующие и полезные стратегии
Для упрощения исследования игр стараются исключить из анализа игры те стратегии, которые при разумном подходе вряд ли могут быть использованы в какой-либо из партий игры. Те стратегии игроков, которые используются или могут быть использованы в какой-либо из партий игры, называются рабочими.
Упрощение заключается в выявлении рабочих стратегий из всех возможных. Так как нас интересуют смешанные стратегии, то рабочие стратегии выбираются с вероятностью, отличной от 0, а не рабочие с вероятностью 0. Для выявления рабочих стратегий используется отношение доминирования (преобладания).
Рассмотрим два
вектора стратегий второго игрока:![]() и
и
![]() .
Величина проигрыша второго игрока
определяется соответственно
.
Величина проигрыша второго игрока
определяется соответственно
![]() и
и
![]() ,
.
Возможны следующие ситуации:
,
.
Возможны следующие ситуации:
Если
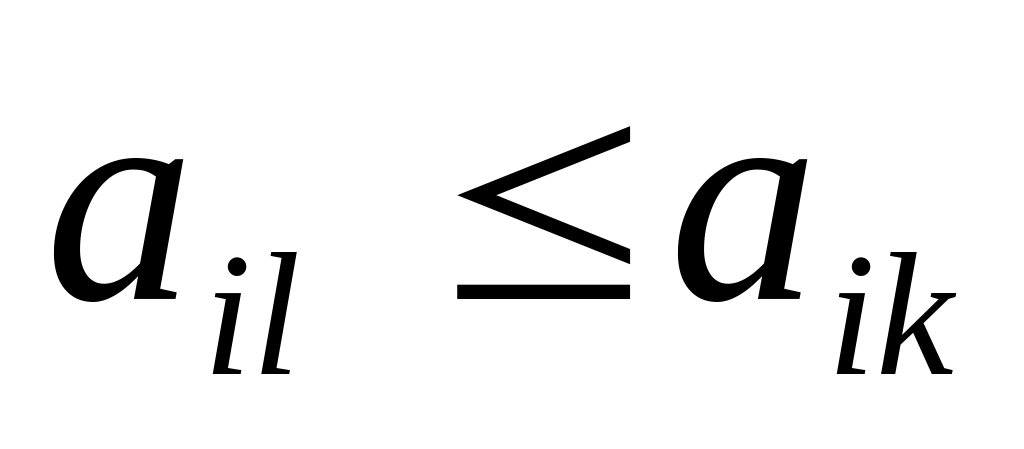 и среди
найдется такое j,
что
и среди
найдется такое j,
что
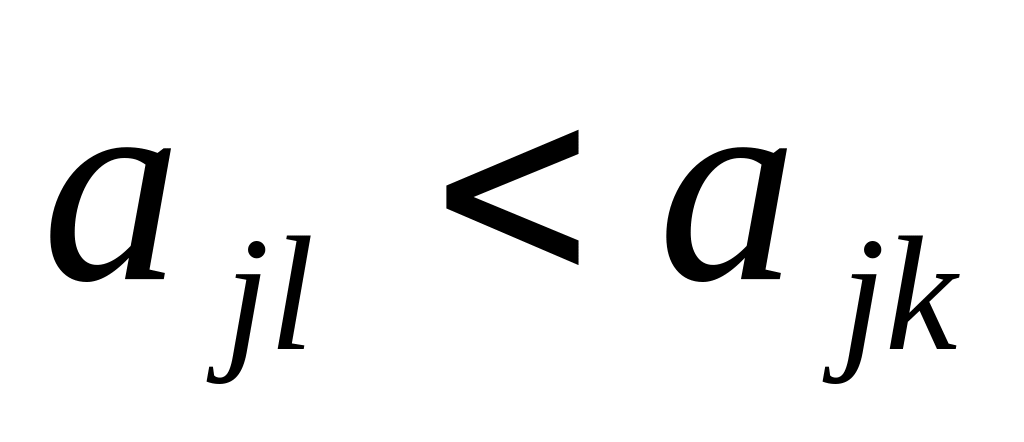 ,
т.е. в матрице игры потери в столбце l
не превосходят соответствующих потерь
в столбце k,
то говорят, что стратегия
доминирует над стратегией
,
т.е. получаем доминирование по столбцам
,
т.е. в матрице игры потери в столбце l
не превосходят соответствующих потерь
в столбце k,
то говорят, что стратегия
доминирует над стратегией
,
т.е. получаем доминирование по столбцам
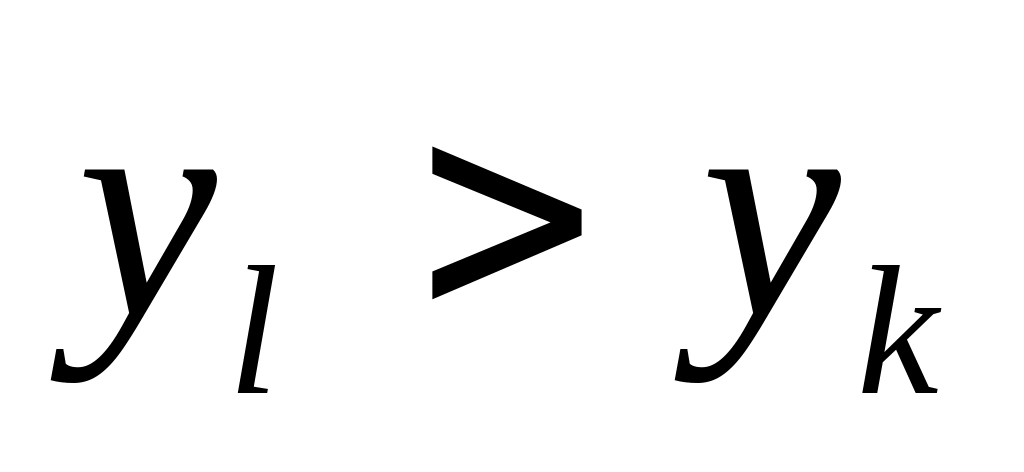 .
В этом случае стратегия
должна быть отброшена, т.е. вычеркнута
из матрицы игры;
.
В этом случае стратегия
должна быть отброшена, т.е. вычеркнута
из матрицы игры;Если же
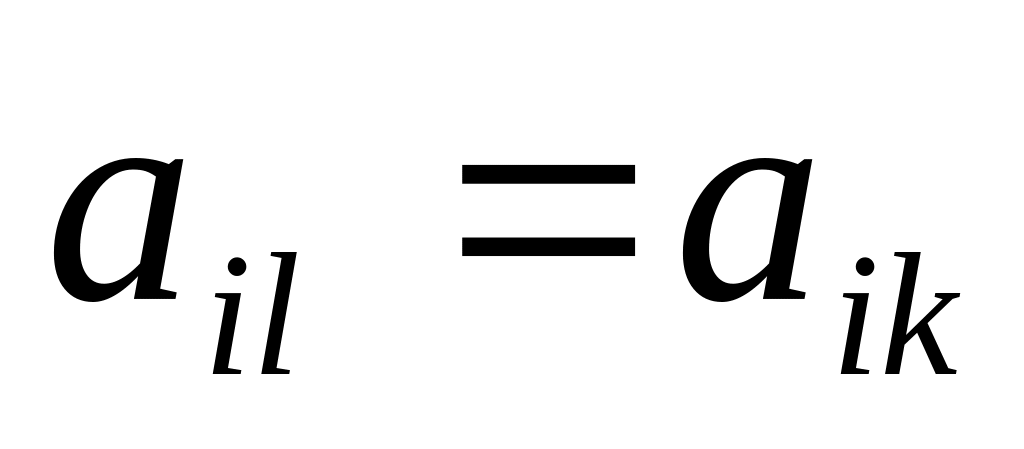 ,
,
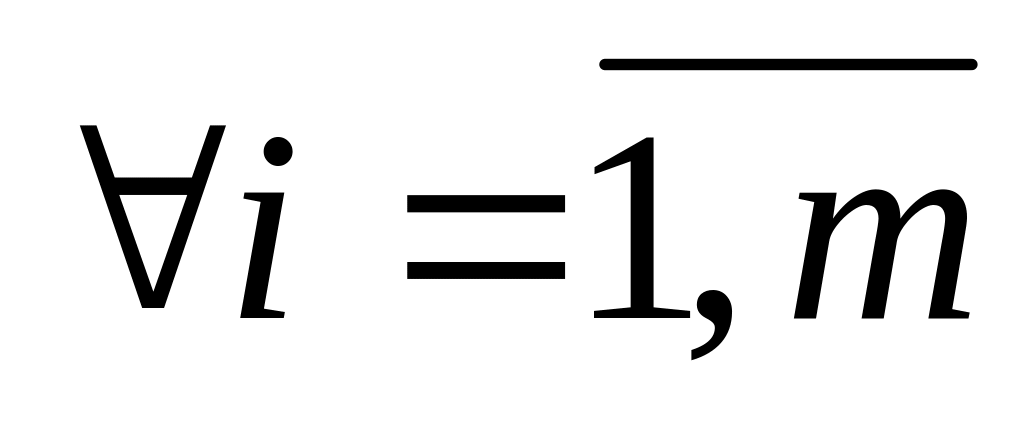 ,
то эти стратегии дублируют друг друга.
,
то эти стратегии дублируют друг друга.
В любом из этих случаев стратегию можно удалять из матрицы без изменения оптимальной стратегии второго игрока.
Доминирующие
стратегии второго игрока имеют наглядную
геометрическую иллюстрацию при переходе
к эквивалентной S-игре
на плоскости. В этом случае
![]() и
и
![]() ,
,
![]() .
.
Н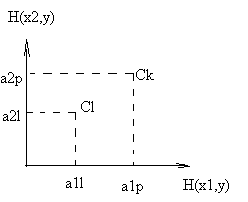 а
рисунке приведены два случая расположения
точек
а
рисунке приведены два случая расположения
точек
![]() и
и
![]() ,
соответствующие чистым стратегиям
и
второго игрока. Легко видеть, что на
рисунке (а)
стратегия
доминирует над стратегией
,
а на рисунке (б)
ни одна из стратегий не является
доминирующей. Для того, чтобы стратегия
доминировала над стратегией
,
точка
должна лежать левее и ниже точки
.
,
соответствующие чистым стратегиям
и
второго игрока. Легко видеть, что на
рисунке (а)
стратегия
доминирует над стратегией
,
а на рисунке (б)
ни одна из стратегий не является
доминирующей. Для того, чтобы стратегия
доминировала над стратегией
,
точка
должна лежать левее и ниже точки
.
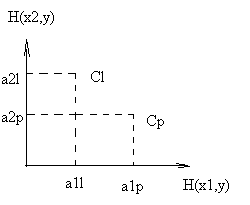
(а) (б)
Аналогичным образом
определяют доминирующие стратегии
первого игрока. Стратегия
![]() доминирует над стратегией
доминирует над стратегией
![]() ,
если выигрыш первого игрока при стратегии
больше выигрышей при стратегии
при любой стратегии y:
,
если выигрыш первого игрока при стратегии
больше выигрышей при стратегии
при любой стратегии y:
![]() ,
,
т.е. если в матрице игры выигрыши в строке больше соответствующих выигрышей строки .
Пример. Предположим, что есть игра
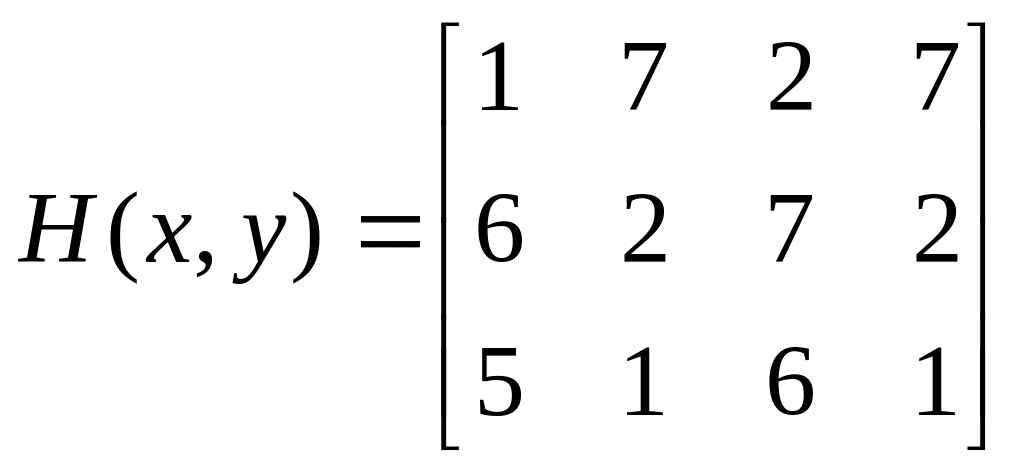 .
.
Воспользуемся отношением доминирования для упрощения игры:
2 и 4 столбцы одинаковые, поэтому получаем игру
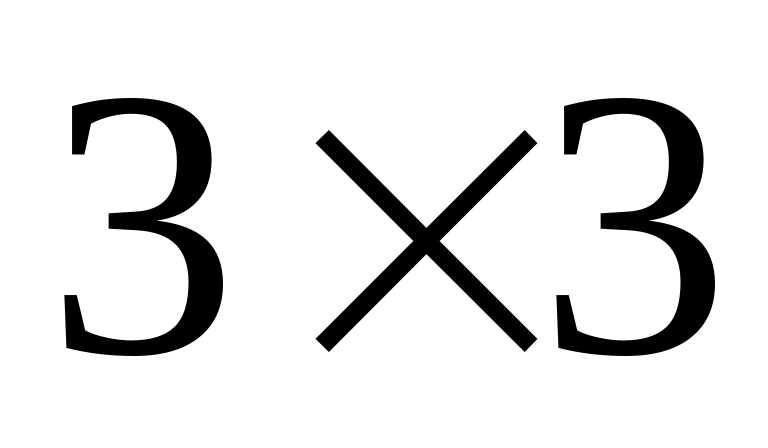 ;
;Сравниваем 2 и 3 строки. Элементы во второй строке превосходят элементы в первой, поэтому первый игрок никогда не будет выбирать 3 стратегию, т.к. вторая принесет ему большую прибыль, значит получаем игру
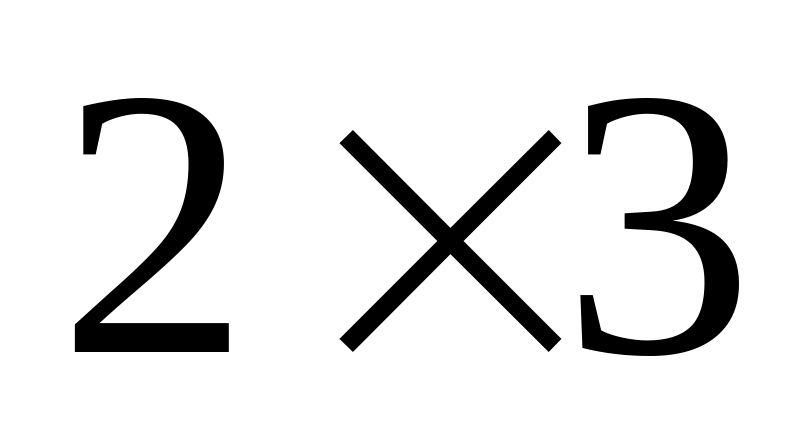 ;
;Сравниваем 1 и 3 столбец,
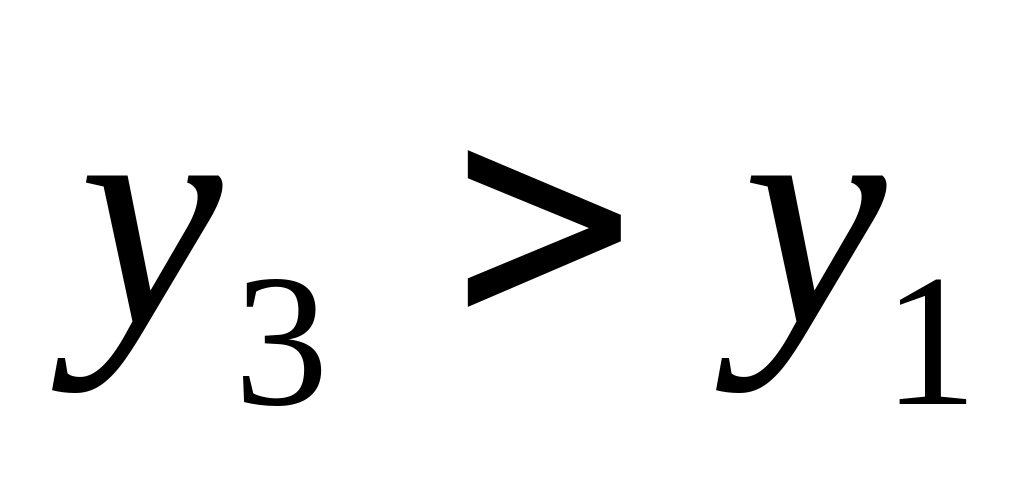 ,
значит получаем игру
:
,
значит получаем игру
:
![]() .
.
Таким образом,
отношение доминирования по строкам
заключается в том, что все
![]() и
и
![]() из
такое, что
из
такое, что
![]() ,
то
,
то
![]() .
.
