
- •Основные понятия теории игр
- •Классификация игр
- •Описание игры в развернутой форме
- •Бескоалиционные игры
- •Приемлемые ситуации и ситуации равновесия в игре
- •Стратегическая эквивалентность игр
- •Антагонистические игры. Общие сведения
- •Чистые и смешанные стратегии
- •Верхняя и нижняя цены игры при использовании смешанных стратегий
- •Основная теорема антагонистических игр.
- •Верхние и нижние цены в s-игре
- •Теорема о минимаксе
- •Геометрическая интерпретация минимакса
- •Решение антагонистических игр. Доминирующие и полезные стратегии
- •Игры с частными случаями платежных матриц
- •Решение матричных игр
- •Линейное программирование для решения матричных игр
- •Графическое решение игр 2*n и m*2
- •Бесконечные антагонистические игры
- •Строго выпуклые игры на единичном квадрате
- •Неантагонистические игры
- •Бескоалиционные игры
Верхние и нижние цены в s-игре
Дальше будем
обозначать S-игру
через
![]() .
Для перехода от игры
к S-игре
вместо пространства смешанных стратегий
второго игрока
.
Для перехода от игры
к S-игре
вместо пространства смешанных стратегий
второго игрока
![]() необходимо использовать пространство
S-стратегий,
т.е. выпуклую оболочку
.
Обозначим потери второго игрока в S-игре
через
необходимо использовать пространство
S-стратегий,
т.е. выпуклую оболочку
.
Обозначим потери второго игрока в S-игре
через
![]() ,
тогда S
— игра зависит от P,
и
,
причем потери
должны быть найдены на скалярном
произведении
,
тогда S
— игра зависит от P,
и
,
причем потери
должны быть найдены на скалярном
произведении
![]() .
Таким образом выражение
.
Таким образом выражение
![]() определяет S-игру.
Функция потерь определяется выражением:
определяет S-игру.
Функция потерь определяется выражением:
![]() .
.
Рассмотрим процедуру оценки верхних и нижних цен в S-игре. Если первый игрок применяет смешанную стратегию , то значение его гарантированного выигрыша
![]() .
.
Обозначим через
![]() такую стратегию первого игрока, при
которой
такую стратегию первого игрока, при
которой
![]() достигает максимума:
достигает максимума:
![]() (эта нижняя цена
игры совпадает с ценой игры в обычной
форме в силу эквивалентности S-игры
с обычной игрой). Стратегию
(эта нижняя цена
игры совпадает с ценой игры в обычной
форме в силу эквивалентности S-игры
с обычной игрой). Стратегию
![]() называют максиминной
стратегией первого игрока.
называют максиминной
стратегией первого игрока.
Предположим теперь,
что второй игрок применяет некоторую
стратегию
.
При этом значение его проигрыша
![]() .
Тогда второго игрока будет интересовать
стратегия:
.
Тогда второго игрока будет интересовать
стратегия:
![]() .
Стратегию
.
Стратегию
![]() называют минимаксной
стратегией второго игрока.
называют минимаксной
стратегией второго игрока.
Таким образом, максиминная стратегия первого игрока определяет нижнюю цену в S-игре:
![]() .
.
Аналогично стратегия
![]() определяет верхнюю
цену в S-игре:
определяет верхнюю
цену в S-игре:
![]() .
.
Выражения для
![]() и
и
![]() можно представить в более удобном виде,
если воспользоваться теоремой.
можно представить в более удобном виде,
если воспользоваться теоремой.
Теорема.
Если S
— произвольная точка m-мерного
пространства и
![]() — многомерная переменная, то имеет
место соотношение
— многомерная переменная, то имеет
место соотношение
![]() .
.
Доказательство.
Пусть
![]() .
Рассмотрим частное значение p,
соответствующее случаю
.
Рассмотрим частное значение p,
соответствующее случаю
![]() при
при
![]() и
и
![]() при
при
![]() .
В этом случае
.
В этом случае
![]() .
Таким образом,
.
Таким образом,
![]() является частным значением скалярного
произведения
,
а значит, подмножеством множества
значений
,
получающихся при всевозможных значениях
p.
На основании теоремы о верхней границе
подмножества находим
является частным значением скалярного
произведения
,
а значит, подмножеством множества
значений
,
получающихся при всевозможных значениях
p.
На основании теоремы о верхней границе
подмножества находим
![]() .
.
С другой стороны,
заменяя в выражении для
значения
![]() на максимальное значение
,
получаем
на максимальное значение
,
получаем
![]() .
.
Это выражение справедливо при любом p. Сопоставляя два последних выражения приходим к соотношению:
. Теорема доказана.
Если воспользоваться доказанной теоремой, то выражение для B(S) можно переписать в виде
![]() .
.
Из этого равенства вытекают два следствия:
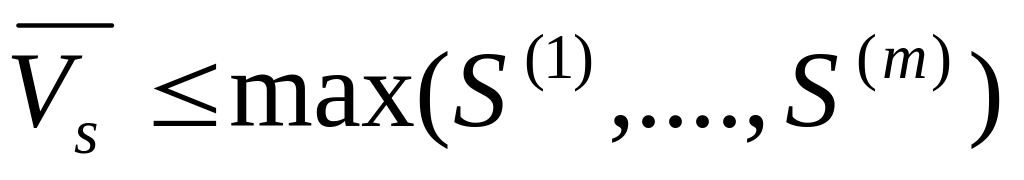 ,
т.е. любая точка
имеет по крайней мере одну координату,
не меньшую, чем верхняя цена игры;
,
т.е. любая точка
имеет по крайней мере одну координату,
не меньшую, чем верхняя цена игры;Если в качестве S взять
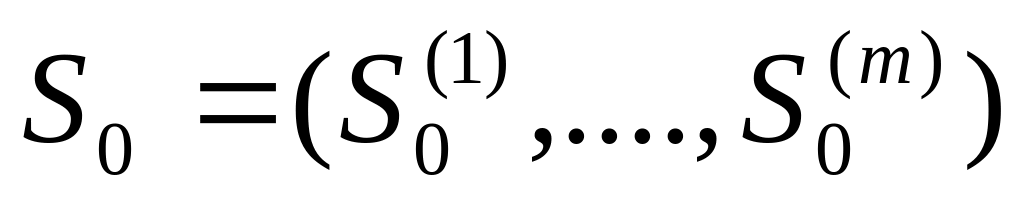 ,
то получим:
,
то получим:
![]() .
Верхняя цена игры равна максимальной
из координат точки
,
определяющей минимаксную стратегию
второго игрока.
.
Верхняя цена игры равна максимальной
из координат точки
,
определяющей минимаксную стратегию
второго игрока.
Теорема о минимаксе
Возможность нахождения каждым игроком своей наилучшей стратегии основывается на следующей теореме, которая может рассматриваться как доказательство существования решения для конечных игр.
Теорема. Всякая конечная антагонистическая игра имеет цену, и у каждого игрока существует по меньшей мере одна оптимальная стратегия.
Исходные предпосылки. Пусть — конечная игра, а — смешанное расширение этой игры. При доказательстве теоремы удобно вести рассуждения в терминах S-игры, поэтому через обозначим эквивалентную S-игру.
Нижняя и верхняя
цены S-игры
будут равны
![]() и
соответственно, независимо от того,
рассматривают игру G
или эквивалентную ей S-игру
,
причем
и
соответственно, независимо от того,
рассматривают игру G
или эквивалентную ей S-игру
,
причем
![]() .
.
Для того, чтобы
доказать теорему, достаточно показать,
что
![]() ,
так как из сравнения с предыдущим
неравенством будет следовать
,
так как из сравнения с предыдущим
неравенством будет следовать
![]() ,
т.е. что игра имеет цену.
,
т.е. что игра имеет цену.
Для доказательства этого неравенства достаточно найти такую смешанную стратегию первого игрока, при которой для всех имеет место
![]() .
(1)
.
(1)
Действительно, если (1) имеет место, то
![]() .
Таким образом, доказательство теоремы
будет сводиться к доказательству
неравенства (1). Доказательство теоремы
опущено (см. напр. Коршунов Ю.М.
Математические основы кибернетики).
.
Таким образом, доказательство теоремы
будет сводиться к доказательству
неравенства (1). Доказательство теоремы
опущено (см. напр. Коршунов Ю.М.
Математические основы кибернетики).
