
- •Основные понятия теории игр
- •Классификация игр
- •Описание игры в развернутой форме
- •Бескоалиционные игры
- •Приемлемые ситуации и ситуации равновесия в игре
- •Стратегическая эквивалентность игр
- •Антагонистические игры. Общие сведения
- •Чистые и смешанные стратегии
- •Верхняя и нижняя цены игры при использовании смешанных стратегий
- •Основная теорема антагонистических игр.
- •Верхние и нижние цены в s-игре
- •Теорема о минимаксе
- •Геометрическая интерпретация минимакса
- •Решение антагонистических игр. Доминирующие и полезные стратегии
- •Игры с частными случаями платежных матриц
- •Решение матричных игр
- •Линейное программирование для решения матричных игр
- •Графическое решение игр 2*n и m*2
- •Бесконечные антагонистические игры
- •Строго выпуклые игры на единичном квадрате
- •Неантагонистические игры
- •Бескоалиционные игры
Чистые и смешанные стратегии
Если игра не имеет седловой точки, то возникают затруднения в определении цены игры и оптимальных стратегий игроков. Рассмотрим, например, игру:
![]()
![]()
B(y)
![]()
В этой игре
![]() и
и
![]() .
Следовательно, первый игрок может
гарантировать себе выигрыш, равный 4, а
второй может ограничить свой проигрыш
5. Область между
.
Следовательно, первый игрок может
гарантировать себе выигрыш, равный 4, а
второй может ограничить свой проигрыш
5. Область между
![]() и
и
![]() является как бы ничейной и каждый игрок
может попытаться улучшить свой результат
за счет этой области. Каковы же должны
быть в этом случае оптимальные стратегии
игроков?
является как бы ничейной и каждый игрок
может попытаться улучшить свой результат
за счет этой области. Каковы же должны
быть в этом случае оптимальные стратегии
игроков?
Если каждый из
игроков применяет отмеченную звездочкой
стратегию (![]() и
и
![]() ),
то выигрыш первого игрока и проигрыш
второго будут равны 5. Это невыгодно
второму игроку, так как первый выигрывает
больше, чем оно может себе гарантировать.
Однако если второй игрок каким-либо
образом раскроет замысел первого о
намерении использовать стратегию
,
то он может применить стратегию
),
то выигрыш первого игрока и проигрыш
второго будут равны 5. Это невыгодно
второму игроку, так как первый выигрывает
больше, чем оно может себе гарантировать.
Однако если второй игрок каким-либо
образом раскроет замысел первого о
намерении использовать стратегию
,
то он может применить стратегию
![]() и уменьшить выигрыш первого до 4. Правда,
если первый игрок раскроет замысел
второго применить стратегию
,
то, используя стратегию
,
он увеличит свой выигрыш до 6. Таким
образом, возникает ситуация, когда
каждый игрок должен хранить в секрете
ту стратегию, которую он собирается
использовать. Однако, как это сделать?
Ведь если партия играется многократно
и второй игрок применяет все время
стратегию
,
то первый игрок скоро разгадает замысел
второго и, применив стратегию
,
будет иметь добавочный выигрыш. Очевидно,
что второй игрок должен менять стратегию
в каждой новой партии, но делать это он
должен так, чтобы первый не догадался,
какую стратегию применит он в каждом
случае.
и уменьшить выигрыш первого до 4. Правда,
если первый игрок раскроет замысел
второго применить стратегию
,
то, используя стратегию
,
он увеличит свой выигрыш до 6. Таким
образом, возникает ситуация, когда
каждый игрок должен хранить в секрете
ту стратегию, которую он собирается
использовать. Однако, как это сделать?
Ведь если партия играется многократно
и второй игрок применяет все время
стратегию
,
то первый игрок скоро разгадает замысел
второго и, применив стратегию
,
будет иметь добавочный выигрыш. Очевидно,
что второй игрок должен менять стратегию
в каждой новой партии, но делать это он
должен так, чтобы первый не догадался,
какую стратегию применит он в каждом
случае.
Секретность можно сохранить, если каждый раз выбирать стратегию случайным образом, используя для этого какой-либо механизм случайного выбора.
Для механизма случайного выбора выигрыши и проигрыши игроков будут случайными величинами. Результат игры в этом случае можно оценить средней величиной проигрыша второго игрока. Вернемся к примеру. Так, если второй игрок использует стратегию и случайным образом с вероятностями 0.5; 0.5, то при стратегии первого игрока среднее значение его проигрыша будет:
![]() ,
,
а при стратегии первого игрока
![]() .
.
Следовательно, второй игрок может ограничить свой средний проигрыш значением 4,5 независимо от стратегии, применяемой первым игроком.
Таким образом, в ряде случаев оказывается целесообразным не намечать заранее стратегию, а выбирать ту или иную случайным образом, используя какой-либо механизм случайного выбора. Стратегию, основанную на случайном выборе, называют смешанной стратегией, в отличие от намеченных стратегий, которые называются чистыми стратегиями.
Дадим более строгое определение чистых и смешанных стратегий.
Пусть имеется игра без седловой точки:
![]() .
Обозначим частоту использования чистой
стратегии
.
Обозначим частоту использования чистой
стратегии
![]() первого игрока через
первого игрока через
![]() ,
,
![]() (вероятность использования i-ой
стратегии). Аналогично обозначим частоту
использования чистой стратегии
(вероятность использования i-ой
стратегии). Аналогично обозначим частоту
использования чистой стратегии
![]() второго игрока через
второго игрока через
![]() ,
,
![]() (вероятность использования j-ой
стратегии). Для игры с седловой точкой
существует решение в чистых стратегиях
(вероятность использования j-ой
стратегии). Для игры с седловой точкой
существует решение в чистых стратегиях
![]() .
Для игры без седловой точки существует
решение в смешанных стратегиях, то есть
когда выбор стратегии осуществляется
на основании вероятностей. Тогда
.
Для игры без седловой точки существует
решение в смешанных стратегиях, то есть
когда выбор стратегии осуществляется
на основании вероятностей. Тогда
— множество чистых стратегий 1-го игрока;
![]() — множество
смешанных стратегий 1-го игрока;
— множество
смешанных стратегий 1-го игрока;
— множество чистых стратегий 2-го игрока;
![]() — множество
смешанных стратегий 2-го игрока.
— множество
смешанных стратегий 2-го игрока.
Рассмотрим пример:
пусть имеется игра
![]()
![]()
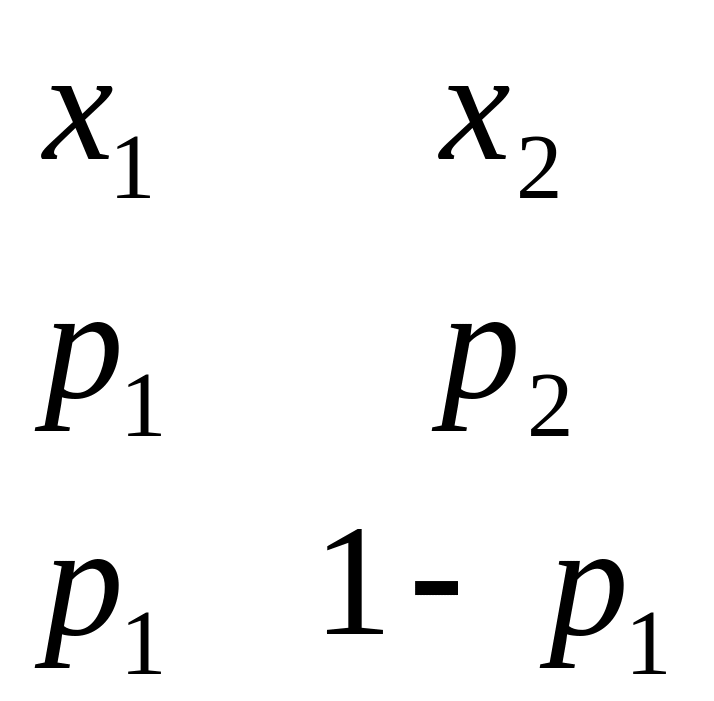
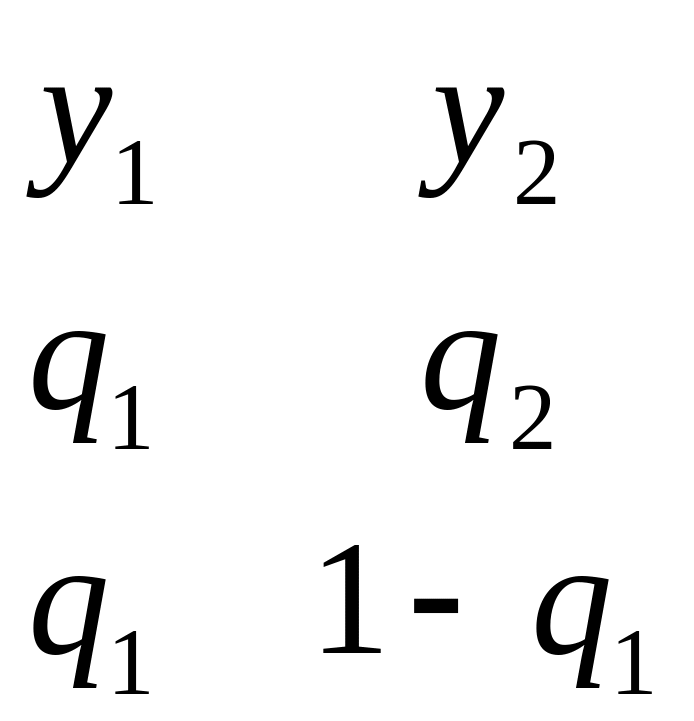
Второй игрок
выбирает вероятность
![]() .
Оценим средний проигрыш второго игрока
при применении им стратегий
и
соответственно:
.
Оценим средний проигрыш второго игрока
при применении им стратегий
и
соответственно:
![]()
![]() .
.
Если первый
применяет свою стратегию
![]() ,
а второй будет применять свою стратегию
,
то
,
а второй будет применять свою стратегию
,
то
![]() будет
определять средний выигрыш первого
игрока:
будет
определять средний выигрыш первого
игрока:
![]() ,
,
![]() .
.
В общем случае
игры
![]() выигрыш первого игрока и проигрыш
второго будет определен:
выигрыш первого игрока и проигрыш
второго будет определен:
![]() ,
,
![]() ,
,
,
,
![]() ,
.
,
.
Опр.:
Игра
![]() называется смешанным расширением игры
.
называется смешанным расширением игры
.
Выигрыш первого игрока в смешанном расширении игры равен проигрышу второго игрока.
