Антагонистические игры. Общие сведения

Опр.: Игра называется антагонистической, если выполняются условия и .

Другими словами, антагонистическая игра — это игра двух лиц с нулевой суммой.

Обозначив множество стратегий первого игрока через X , а множество стратегий второго игрока через Y , антагонистическую игру можно описать следующим образом:

, где — выигрыш первого игрока или проигрыш второго.

Как отмечалось выше, целью исследования является нахождение ситуации равновесия (равновесия в прямом конфликте). Поэтому поведение игроков диктуется:

1-ый игрок старается за счет выбора стратегии максимизировать свой выигрыш ( );

2-ой игрок за счет выбора стратегии старается минимизировать проигрыш ( ).

Суть этого конфликта состоит в том, что каждый из игроков обладает возможностью менять только свою стратегию. Преодоление этой трудности, другими словами определение наиболее рационального способа поведения игроков в этой игре, это и есть игровая модель принятия решений.

Если в антагонистической игре двух лиц множества X и Y конечны, то игра называется матричной. Название объясняется тем, что игру можно представить таким образом: элементы множеств X и Y занумеровываются, например:

и .

Ситуацией в этом случае является пара , , . Выигрыш первого игрока рассматривается как элемент матрицы А размером Эта матрица называется матрицей игры. Игра протекает следующим образом: игроки одновременно и независимо друг от друга называют номер строки (первый игрок) и номер столбца (второй игрок). Элемент матрицы, расположенный на пересечении выбранных строки и столбца, и есть выигрыш первого игрока и соответственно проигрыш второго.

Рассмотрим матричную антагонистическую игру с матрицей выигрышей:

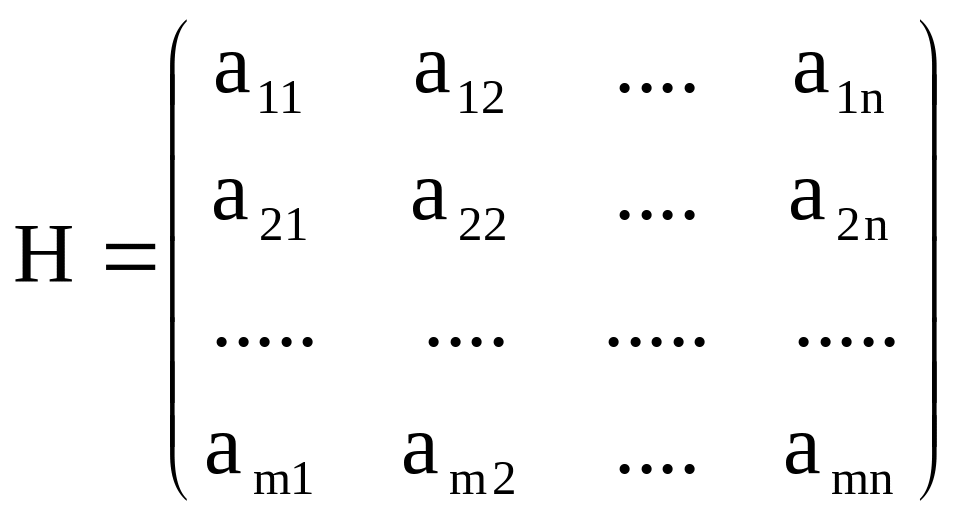
Первый (максимизирующий) игрок выбирает строку. Второй (минимизирующий) игрок выбирает столбец, на их пересечении записан выигрыш первого игрока. Каждый игрок стремится к увеличению своего выигрыша. Но его выигрыш зависит не только от его выбора, но и от того, какая стратегия будет выбрана противником. Поэтому, стремясь получить максимальный выигрыш, каждый игрок должен учитывать поведение противника. В теории игр выбор оптимальной стратегии предлагается осуществлять, основываясь на принципе минимакса (максимина), который иногда называют «принципом осторожной игры против умного партнера».

Вот рассуждения первого игрока, основанные на указанном принципе. «Пусть я выбрал i-ую строку. Тогда самое меньшее, на что я могу рассчитывать, будет . Поэтому естественно выбрать такую строку, чтобы этот минимальный выигрыш был наибольшим: . Таким образом, я могу гарантировать, что меньше, чем , мой выигрыш быть не может».

Эта величина называется нижним значением игры и обозначается:

.

Номер строки i, который выбрал первый игрок, называется максиминной стратегией первого игрока.

Рассуждения второго игрока, основанные на принципе минимакса. «Пусть я выбрал j-ый столбец. Тогда самое большее, что я могу проиграть — это . Поэтому естественно выбрать такой столбец, чтобы этот максимальный проигрыш был наименьшим, т.е. чтобы . Таким образом, я мог бы гарантировать, что меньше, чем , мой выигрыш быть не может».

Величина называется верхним значением игры и обозначается:

.

Значение j называется минимаксной стратегией 2-ого игрока.

Теорема: Если - антагонистическая игра, то для любого , имеет место:

Доказательство:

Так как по определению , то, очевидно, . Так как , то . Эти неравенства очевидны для любых x, y и для тех, которые обеспечивают верхнюю и нижнюю цены игры:

.

Таким образом, . Теорема доказана.

Пример. Имеется следующая платежная матрица

A(x)

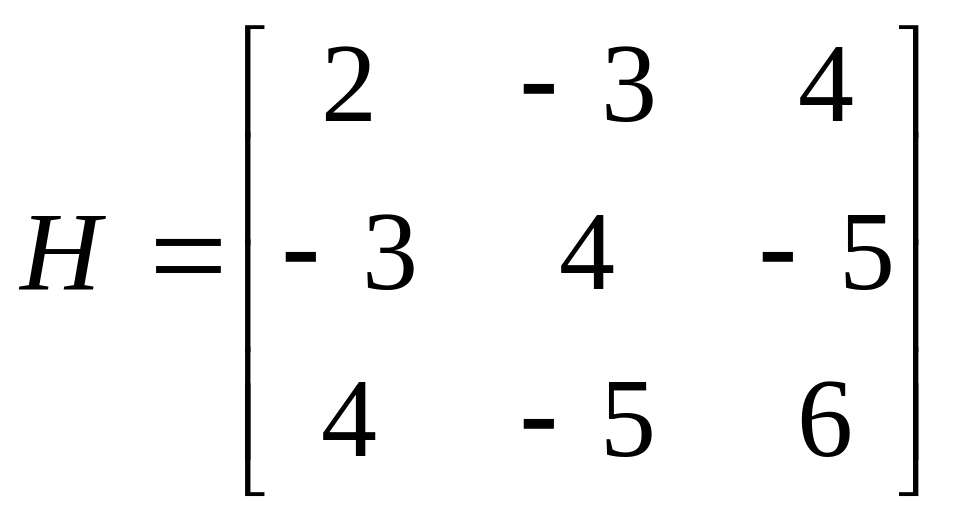
B(y)

Нижняя цена игры равна -3, верхняя цена игры равна 4, максиминная стратегия первого игрока есть , минимаксная стратегия второго игрока есть .

Если нижняя цена игры равна верхней цене игры, то игра называется игрой с cедловой точкой. Пусть , тогда величину с называют ценой игры, а стратегии игроков, обеспечивающие результат с, — оптимальными стратегиями. Клетку матрицы, определяющую величину с, называют седловой точкой, так как значение с является одновременно минимальным элементом строки и максимальным элементом столбца, на пересечении которых стоит эта величина.

Любая седловая точка является искомой точкой равновесия в игре, так как любое отклонение игроков от оптимальной стратегии приведет к уменьшению выигрыша первого, либо к увеличению проигрыша второго.

— цена игры. Если , то игра является несправедливой, т.к один игрок точно проигрывает. Если , то игра справедливая. Для того чтобы сделать несправедливую игру справедливой, первый игрок должен уплатить второму игроку величину с перед началом каждой новой партии.