2.2.2. Мультипликативные байесовские алгоритмы и их частичная

ПАРАМЕТРИЗАЦИЯ

Случайные реализации выборок сводятся в ряде случаев к совокупностям подвыборок у_v, v = с независимыми случайными флюктуациями. Это имеет место при сочетании узкополосного зондирования с широкополосным или многочастотным, при многопозиционной работе и т.д. В соответствии с правилом перемножения вероятностей алгоритмы (2.6) можно привести к мультипликативной форме:

(2.7)

(2.8)

Вариант алгоритма (2.8) следует из варианта (2.7) после деления оптими­зируемого выражения на произведение не зависящих от i и не влияющих, следовательно, на оптимизацию условных плотностей вероятности .

Частичная параметризация алгоритмов (2.7) - (2.8) связана с тем, что часть подреализаций , используют обычно для измерения па­раметров цели как признаков ее распознавания. Если известны априорные плотности вероятности распределений параметра для каждого i-го класса объектов, то входящие в (2.7) функции правдоподобия решений о классах можно связать с функциями правдоподобия значений парамет­ра , так что

(2 .9)

Функция же правдоподобия значений параметра связана с послеопытной плотностью вероятности его значений Эта связь

(2.10)

вытекает из формулы умножения вероятностей при совмещении событий y_v и .

Входящую в (2.10) величину С_v поcле приема реализации y_v при изме­рении по максимуму правдоподобия можно считать фиксированной вели­чиной. Действительно, значение p(y_v) после приема реализации y_v фиксиро­вано. В условиях же измерения по максимуму правдоподобия (безотносительно к гипотезам о значениях i) допустимо принять .

Если ввести плотность вероятности f(ε) ошибок измерения , то входящую в (2.9) послеопытную плотность вероятности значений парамет­ра можно представить в виде

В силу (2.9) - (2.10) функции правдоподобия решений о классе можно придать вид

(2.11)

Согласно (2.11) она пропорциональна значению для априорной плотности вероятности оценок параметра с учетом ошибок измерения: Значение определяется интегралом свертки

В нем – априорная плотность вероятности значений параметра. При идеально точном измерении где - дельта-функция. Тогда = и

Алгоритмы распознавания (2.7) – (2.8) заменяются в результате пол­ученных соотношений (2.9) – (2.11) единым мультипликативным алгорит­мом:

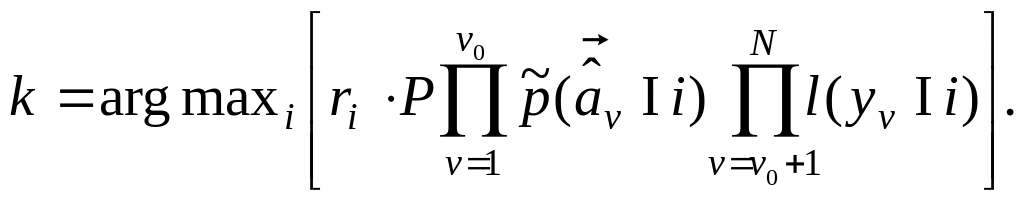(2.12)

Из него исключены, как и ранее, не зависящие от i множители заключен­ного в квадратные скобки выражения. Знаки "тильда" при априорных плотностях вероятности параметров (признаков распознавания) учитывают, как и в (2.11), конечную точность оценок .

Обычно векторный признак , оцениваемый по некоторой реализации y_v, разбивается на несколько скалярных и векторных признаков с неза­висимыми их флюктуациями и флюктуациями их оценок. Сомножители первого из произведений (2.12) сами становятся тогда произведениями нескольких аналогичных сомножителей. Чтобы не усложнять формулу (2.12), условимся сохранять ее вид и в этом случае, условно сводя увеличение общего числа признаков к увеличению числа независимых подреализаций v₀ и N.