Invitation to a Contemporary Physics (2004)

rarely occur in our sensible world and hence an object only of mathematical curiosity. This notion is, however, erroneous. Chaos is a robust phenomenon that persists over a wide range of values of the control parameters. The sensitive dependence on initial conditions does not wash easily. Chaos is, therefore, not rare. Indeed, the contrapositive is true. Nature is full of it. Almost any real dynamical system, driven hard enough, turns chaotic. Looking for a chaotic system is like looking for a non-elephant animal! Most animals are non-elephant.

The most celebrated example of chaos is, of course, fluid dynamical turbulence — the last unsolved problem of classical physics. Great physicists of the 20th century have bemoaned, ‘Why turbulence’? We see turbulence in jets and wakes, in water flowing through pipes and past obstacles. As the flow rate (the control parameter) increases beyond a critical value, and this is the meaning of the phrase ‘driven hard enough,’ the smooth laminar flow becomes unstable. It develops waviness and quickly turns into a complex, almost random pattern of flow, live with swirling eddies of all sizes as we move downstream. The flow pattern is aperiodic — it never repeats itself. This is fully developed turbulence. We can demonstrate this easily by injecting a marker dye in the flow tube, that makes the flow pattern visible to the eye (See Fig. 7.1a).

At the onset of turbulence the otherwise fine and straight thread of marker dye undulates wildly and quickly disrupts into a complex ramified pattern, down to

(a)

(b)

(c)

Figure 7.1: Examples of instabilities leading to chaos: (a) turbulence in pipe flow marked by a dye; (b) convective instability showing cylindrical rolls and their wobbling; and (c) rising smoke column developing whorls.

length scales too fine for the eye to discern, making the water appear uniformly colored as we move downstream — as if through thorough mixing. The threshold condition for the onset of this instability can be conveniently expressed in terms of a dimensionless control parameter called the Reynolds number (R), after the great fluid dynamicist Osborne Reynolds. The Reynolds number R = ULρ/η, where U is the typical flow velocity (or rather variation of velocity), L the tube diameter (or length scale over which the velocity variation takes place), ρ the fluid density and η the fluid viscosity (treacliness). Turbulence sets in for R greater than a critical value Rc, which is about 2000 for water, but can be as high as 105 if the flow is increased very gently and the pipe is very smooth. (This is something like the superheating of water beyond its boiling point.) It is clear that the critical Reynolds number Rc is not a universal number. It depends on the geometry of the problem, whether the tube cross-section is circular or elliptical, for instance. But importantly, the sequence of flow patterns, or the route to turbulence turns out to be universal — within a class. (This is very reminiscent of the universality class of a second order phase transition. Thus, di erent ferromagnets have di erent Curie (critical) temperatures. But the behavior of magnetization near the critical point is universal within a wide class. These are deep problems.)

Another example of chaos that has played a decisive role in the experimental and theoretical study of turbulence-as-chaos is the Couette–Taylor instability problem. Here, the fluid is contained in the annular space between two long co-axial circular cylinders, one of which, usually the inner one, is made to spin. At low spin rates the fluid is dragged viscously around by the inner cylinder and there is a time independent laminar flow in the form of rotating circular cylindrical sheets. Beyond a critical spin rate, however, this laminar flow becomes unstable (the Couette–Taylor instability) and the circular cylindrical flow sheets develop undulations in the form of a stack of doughnuts or tori. A single independent frequency of oscillation appears. At a still higher spin rate another independent frequency appears making the system doubly periodic. As the spin rate is increased still further, the pattern suddenly jumps to a chaotic one. Again the threshold condition is non-universal but the route to chaos, the sequence of patterns, defines a universality class. This seems di erent from that of the pipe flow discussed above. We should note that the Couette flow is a closed one: the flow feeds back on itself. In contrast to this, the flow in a jet or wake is an open flow where the turbulence develops as we move downstream. It does not close on itself.

Yet another example of chaos is provided by the convective flow of a fluid mass which is heated from below. In fact this was the example that E. N. Lorenz studied so intensively as a model of his ‘toy weather’ that he had simulated on his computer, a Royal McBee, at MIT way back in 1963. His paper entitled ‘Deterministic Non-periodic Flow’ (published in the Journal of Atmospheric Sciences, Vol. 20, pp. 130–41, in 1963 ), laid the foundation of the modern science of chaos. It was here that he had observed the sensitive dependence on initial conditions that makes

long-range weather forecast impossible. The great French mathematician Henri Poincar´e had hinted at such a sensitive dependence in 1903! (It is a sobering thought that Lorenz did all his simulations on a Royal McBee, a vacuum-tube based computer capable of doing just about 60 multiplications a second — a snail’s speed compared to the modern Cybers and Crays capable of hundreds of millions of floating point operations a second.)

Returning now to our convection cell, nothing much happens if the temperature di erence is small enough. Heat is simply conducted to the cooler top surface through molecular di usion. At a higher critical temperature di erence, this steady state becomes unstable (the Rayleigh–B´enard instability) and cylindrical rolls of convection develop in our cell, assumed to be rectangular for convenience (see Fig. 7.1b). This happens when the forces of buoyancy overcome the damping e ects of viscous dissipation and thermal di usion. Heated fluid at the bottom expands, and thus made lighter, ascends along the center to the cooler top layers, delivers heat there and then moves out and down the sides, completing the roll. On further heating beyond a threshold, this pattern becomes unstable and the rolling cylinders begin to wobble along the length. More complex flow patterns appear successively, cascading to a point of accumulation at which the flow becomes turbulent. The route to chaos (turbulence) is the so-called period-doubling bifurcation that we will discuss later. Incidentally, the control parameter in this case is the dimensionless Rayleigh number Ra = gραh3∆T/ηκ, where g = acceleration due to gravity, κ = thermal conductivity, α = coe cient of thermal expansion, h = height of cell, and ∆T the temperature di erence. The first instability sets in when Ra exceeds a critical number that depends on the geometry, e.g., the aspect ratio of the cell. Convectional instability is common in Nature. On a hot summer’s day one cannot fail to observe the pattern of clouds imprinted on the sky by the rising convectional currents.

There is an amusing example of turbulence that you can readily observe if you are a smoker, or have a smoker friend willing to oblige. The column of smoke rises from the lighted tip straight up to a height and then suddenly disrupts into irregular whorls (see Fig. 7.1c). Here again the hot smoke rises faster and faster through the cooler and so denser air until it exceeds the critical Reynolds number and turns turbulent. It is really no di erent from an open jet.

The examples of chaos cited above are all from fluid dynamics — turbulence. But chaos occurs in the most unexpected places. It is revealed in the ECG traces of patients with arrhythmiac hearts and the EEG traces of patients with epileptic seizures. It is suspected in the apparently random recurrence of certain epidemics like measles. It lurks in the macroeconomic fluctuations of commodity and stock prices. It is seen in chemical reactions and in the populations of species competing for limited resources in a given region. The irregular pattern of reversals of Earth’s magnetic field is suspected to be due to the chaotic geodynamo. Chaos is, of course, well known in nonlinear electrical oscillators — the classic Van der Pol oscillator

and lasers, where chaos masquerades as noise. Chaos is implicated in the orbits of stars around the galactic center. The list is endless. But most of these examples suggest that chaos requires an interplay of a large number of degrees of freedom. Is this really so?

7.1.3Can Small be Chaotic?

Small here means smallness of the number of degrees of freedom that the dynamical system may have. A number as small as three, say. Can such a small system exhibit the apparent randomness that we associate with chaos? Chaos, as we have seen in the case of turbulence, means on aperiodic flow with a long-range unpredictability about it. The flow pattern must not repeat itself at the very least. Can a system with a small, indeed finite, number of degrees of freedom be so ‘infinitely inventive’ of the flow patterns as to go on surprising us forever without exhausting its stock of possibilities and without having to repeat itself? That is the question. And the answer that has emerged slowly but surely over the last three decades or so is that it can, provided there is nonlinearity in it. This is a necessary condition. Dissipation will help — it is there in all real systems anyway. This view disagrees sharply with the ideas about turbulence that have prevailed since the time of the great Soviet physicist L. D. Landau. Landau’s paradigm for turbulence visualized a sequence of an infinite number of competing oscillations with incommensurate frequencies, emerging one at a time as the control parameter crossed the successive thresholds of instabilities. So it is ‘infinite’ versus ‘finite.’ To appreciate this fully let us examine some of the examples of chaos mentioned above more carefully.

The examples of chaos we have described so far are mostly about turbulence in fluids. It is clear that the fluid flow is described completely by Newton’s laws of motion. Of course, they have to specialize, to the case of the fluid continuum where they take on the form of the macroscopic equations of fluid dynamics — the Navier–Stokes equations. This equation simply expresses the law that mass times acceleration of an element of fluid equals the net force acting on it due to the di erence of pressures fore and aft, and the viscous drag on the sides. (Viscosity of course, implies dissipation of energy that will cause the motion to die down, unless kept alive by an external driving agency, the rotating inner cylinder in the Couette flow for instance.) How can such a deterministic system exhibit the apparent randomness of turbulence. The idea that goes back to Landau is this. The fluid has infinitely many degrees of freedom. How? Well, at each point of space the fluid can move up and down, right and left and forward and backward. That is three degrees of freedom. There are infinitely many points in any finite volume and that adds up to an infinite number of degrees of freedom.

It is often convenient to combine these local point-wise degrees of freedom distributed in space into extended oscillations or waves, called modes, of di erent wavelengths and talk in terms of these infinite number of modes instead. It is just

as a wave on the surface of water is made up of movements of the elements of water all over the surface. Conversely, the movement of the fluid at any given point can be re-constituted from the superposition of these waves. The two descriptions are completely equivalent and are related by what mathematicians call the (spatial) Fourier Transform. Likewise, a flow at a point fluctuating in time can be regarded as a superposition of periodic oscillations of di erent frequencies through a temporal Fourier transform — giving a frequency spectrum. The strength of the di erent Fourier components gives the power spectrum of the flow.

This then is the infinite number of oscillations or modes of the fluid that Landau invoked to describe turbulence. As the frequencies are incommensurate, the flow is only quasiperiodic, never quite repeating itself. Two frequencies are said to be incommensurate if their ratio is irrational, i.e., it cannot be expressed as a ratio of two whole numbers. A fully developed turbulence has infinitely many such frequencies making the flow aperiodic for all practical purposes. The power spectrum is then a continuous one with no dominant sharp frequencies in it. This is what chaos is. This aperiodicity can be roughly appreciated with the help of a simple example. Imagine a system with a large number, 26 say, of simple pendulums of periods 0.5, 0.6, 0.7, . . ., 2.8, 2.9, 3.0 seconds and let them go simultaneously from the right of their equilibrium positions. Some thought and arithmetic will show that it will take 7385 years before the system repeats its initial state! And that when the frequencies (or the periods) are still commensurate, and finite in number. Incommensurate frequencies will push this recurrence time to eternity. (This is much like the problem of finding the recurrence time for a planetary alignment in the solar system — the syzygy problem of finding the lowest common multiple, of course).

This scenario for turbulence, and for chaos in general, seems eminently appealing but has really never been put to the test. No-one has seen this route to turbulence via the successive emergence of these infinite number of mode frequencies. Perhaps it applies to open flows — jets and wakes. On the contrary, there are known examples of turbulence that refute it. The Couette flow as discussed above is a case in point. So is the case with the convective flow which was modelled by Edward Lorenz by a finite number, in fact three, of interacting macroscopic degrees of freedom. It showed chaos in no uncertain terms. And the route to this convective chaos was studied experimentally in an ingenious experiment on a liquid helium cell by Albert Libchaber, and was found to be of the period-doubling kind, quite di erent from that of Landau, as we shall see later. In any case there are a number of computer models with small numbers of degrees of freedom that show chaos. The question is what makes them chaotic. The answer lies in nonlinearity. The Navier–Stokes equations are nonlinear.

Nonlinearity is a mathematical way of saying that the di erent dynamical degrees of freedom act on each other and on themselves so that a given degree of freedom evolves not in a fixed environment but in an environment that itself

changes with time. It is as if the rules of the game keep changing depending on the present state of the system. A simple example will illustrate what we mean. Take y = ax, a linear relation. Changes in y are proportional to those in x, the constant of proportionality being ‘a.’ In this game the e ect is proportional to the cause, and the controlling parameter ‘a’ is fixed. Now consider y = ax2. Here the e ect is proportional to the square of the cause. We may rewrite this in the old form as y = (ax)x and say that the parameter controlling the game, namely (ax) itself depends on x. This is nonlinearity, or nonlinear feedback if you like. In point of fact, interactions that are linear in the state variables are no interactions at all. One can re-define new state variables as linear combinations of the old ones such that these new state variables do not interact at all. This is called normal mode analysis. It is the nonlinearity that makes for the complex behavior — in particular it can generate the sensitive dependence on the initial conditions. It can amplify small changes. One does not need an infinite number of degrees of freedom.

But you may turn around and say that the fluid dynamical system does have an infinite number of degrees of freedom anyway. Well, this is where dissipation (friction) comes in handy. It turns out that all but a few of these get damped out rather quickly by this friction, and the system settles down to the few remaining, macroscopic degrees of freedom that really define its state space. As we will see later, we need a minimum of three to have chaos in a continuous flow.

A final worry now. A dynamical system with a small number of degrees of freedom will have a low dimensional state space. Moreover, the degrees of freedom are expected to have a finite range — we don’t expect the velocities to be infinite for example. Thus the phase point will be confined to a finite region of the low dimensional state space. This raises a geometrical question of packing. How does the phase trajectory, confined to a finite region of the low dimensional state space, wind around forever without intersecting itself or closing on itself? There is an ingenious geometrical construction that illustrates how this is accomplished. We know that two trajectories from neighboring points diverge, stretching the line joining them exponentially. But this cannot go on indefinitely because of the finiteness of the range. The trajectories must fold back, and may approach each other only to diverge again (Fig. 7.2).

This will go on repeating. This process of stretching and folding is analogous to a baker’s transformation. He rolls the dough to stretch it out and then folds it, and then repeats the process again and again. We can drop a blob of ink on the dough to simulate a dust of phase points. The process of stretching and folding will generate a highly interleaved structure. In fact after a mere two dozens or so iterations we will have a 224 layers and thus a fine structure down to atomic scales. The inky spot would have spread out throughout the dough coloring it apparently uniformly, suggesting thorough mixing. Yet, actually it is finely structured. The neighboring points on the inky spot would have diverged out and become totally uncorrelated after a few rounds of the baker’s transformation. Indeed, stretching with folding is a highly nonlinear process that generates the above sensitivity. The

2

1

(a)

2 1

(b)

Figure 7.2: Sensitive dependence on initial conditions: (a) divergence and, (b) divergence-cum- folding-back of neighboring trajectories.

baker’s transformation seems to be a general algorithm for chaotic evolution.

Our discussion so far has centered on some deep philosophical questions about and a general qualitative understanding of chaos. We will now turn to a simple but real, in fact household experiment with chaos that should be refreshing.

We are going to experiment with a leaking faucet! We will be following here the idea of Robert Shaw of the University of California, Santa Cruz.

7.2 Lesson of the Leaking Faucet

Leaky faucets are known universally. They are perhaps best known as a very e ective form of torture as many an insomniac waits attentively for the next drop to fall. It is, however, less well known that there is a universality to their pattern of dripping as the flow rate is turned on gradually and su ciently. There is some pretty physics involving this. It also happens to be rather easy to experiment with. All you need is a leaky faucet, preferably one without a wire mesh, and a timing device to monitor the time intervals between successive drops as the flow rate (our control parameter) is gradually increased. Unfortunately, the time intervals can get rather short, of the order of a fraction of a second, down to milliseconds and even

242 Chaos: Chance Out of Necessity

Time

Figure 7.3: Leaking faucet dripping with single period T0 at low flow rate.

microseconds, just when interesting things begin to happen. We will, therefore, have to employ detectors other than our unaided eyes and ears. We could, for instance, use a microphone to pick up the sound signals of the falling drops, or better still, arrange to have the falling drop interrupt a beam of laser (or ordinary) light and detected by a photodiode. The data can then be acquired by and stored on a PC, which has now become part of the science kit in most high schools. At low enough rate of flow, the faucet leaks with a monotonous periodicity — drip, drip, drip, . . . .

The successive drops fall at equal intervals, T0 say (Fig. 7.3).

This dripping pattern persists up to a fairly high threshold flow rate. The time interval T0, of course, gets shorter and shorter. At and beyond this threshold, however, this pattern becomes unstable and a new pattern emerges — pitter-patter- pitter-patter · · · (Fig. 7.4). The intervals between successive drops become unequal now. We have a short interval T1 alternating with a long interval T2, generating thereby a sequence T1, T2, T1, T2, . . . . We say that the period has doubled. The original single period T0 has bifurcated into a pair of unequal periods T1, T2. The repeat ‘motif’ now consists of a pair of two successive periods, one long and the other short. Note that the period-doubling refers to this two-ness, and not to the absolute value of the time interval, which, if anything, only gets shorter as the flow is turned up progressively. This new pattern in turn persists up to a still higher threshold, and then becomes unstable. There is a period doubling again: Each of the intervals T1 and T2 bifurcates into two unequal intervals, leading to the pattern T3, T4, T5, T6, T3, T4, T5, T6, . . . . Let us summarize our findings so far. We

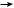
T1 T2 T1 T2 T1

Signal

Time

Figure 7.4: Leaking faucet dripping with doubled period (T1, T2) at a higher flow rate.

started with period 1 (= 20), which bifurcated to period 2 (= 21) and which in turn bifurcated to period 4 (= 22). The trend continues. At the nth bifurcation, we get the period 2n. It turns out that the successive bifurcations come on faster and faster in terms of the control parameter (the flow rate) and they pile up at a point of accumulation as n → ∞ (infinity). This is the critical value of our control parameter. At this point, the period becomes 2∞, which is infinite. The dripping pattern never repeats itself. It has become aperiodic. It is as if the drops fall to the beats of an infinitely inventive drummer. This is chaos. We have just discovered a period-doubling route to chaos!

The chaos is robust and it has a universality about it that we will discuss later. Thus, you can change the faucet; you can replace water with beer if you like; you can add some surfactants to reduce its surface tension or whatever. The perioddoubling sequence will still be there, and many numbers characterizing the approach to chaos will remain unchanged. This is reminiscent of the universality familiar from the critical behavior of second-order phase transitions.

What happens if we push our control parameter beyond this critical value. Well, the aperiodic chaos persists but there are now finer structures such as the appearance of narrow windows of periodicities, that we cannot pause to discuss here.

It is amazing that a simple-looking system such as a leaking faucet should reveal such complexity, or conversely, that chaos should hide such simplicity. We will now turn to a more quantitative description of chaos.

7.3 A Model for Chaos

Now that we have experimented with chaos, let us make a simple model of it that we can play around with, and hopefully solve it in the process. Solving here requires no more than elementary operations of addition, multiplication and raising to power (exponentiation), done repeatedly (that is iteratively), all of which can be entered easily on a hand-held calculator. In fact this is precisely what was done by Mitchell J. Feigenbaum of the Los Alamos National Laboratory in the early seventies using his HP-65 hand-held calculator. And that made the study of chaos such a refreshing exercise with numbers, and, of course, led to many a breakthrough.

7.3.1 The Logistic Map

The model we are going to study is the so-called logistic map or equation: Xn+1 = bXn(1 − Xn). It is an algorithm, that is, a rule for the growth of a quantity ‘X’ controlled by a growth factor ‘b.’ Given the value Xn of this quantity at the nth instant, or go-round, all you have to do is to substitute this value in the right-hand side expression, evaluate it and voila! You have the value of X at the (n + 1)th go-round, namely Xn+1. You can iterate this process and thus generate the value of X at any future instant, starting from an initial value X0, called the seed. This