1. Уравнения Гиббса–—–Гельмгольца:
U = F – T(¶F/¶T)V ; H = Ф – T(¶Ф/¶T)p. (4.1)
Для их получения следует записать U = F + TS, H = Ф + TS и подставить соответствующие выражения для энтропии. Кроме того‚ можно написать‚ например‚
(4.2)
2. Соотношение между коэффициентами термического уравнения состояния. Напомним‚ что уравнение‚ выражающее внутреннюю энергию как функцию внешних переменных и температуры‚ называется калорическим уравнением состояния‚ а уравнения состояния‚ выражающие таким же образом термодинамические силы‚ называются термическими. В нашем случае это единственное уравнение p = p(V,T).
Правило (4) непосредственно записано для этого уравнения‚ и из него немедленно следует:
p’T = a /bT = a KT. (4.3)
Mодуль объемной упругости и сжимаемость‚ конечно‚ связаны правилом (2): bT = 1/KT (и аналогично bS = 1/KS ). Эти две взаимно обратные величины включены в таблицу потому‚ что на практике часто используют и ту‚ и другую.
Для идеального газа KT = p‚ a =1/Т‚ p’T = p/Т.
3. Соотношения взаимности (Максвелла). Эти соотношения получаются применением правила (6) к дифференцированию каждого потенциала по его естественным независимым переменным с последующим учетом уравнений состояния для сопряженных с ними переменным (приведены в таблице). Имеем
(¶T/¶V)S ={(6) для U}= – (¶p/¶S)V, (4.4)
(¶S/¶V)T ={(6) для F}= (¶p/¶T)V , (4.5)
(¶T/¶p)S ={(6) для H}= (¶V/¶S)p, (4.6)
(¶S/¶p)T ={(6) для Ф}= – (¶V/¶T)р , (4.7)
4. Разность между изобарной и изохорной теплоемкостями. Задачу можно также сформулировать иначе: выразить Ср через CV. Удобно начать с выражения nCp = Т(¶S/¶T)p. Дальнейший путь сначала очевиден:
ѕ®
Первое из подчеркнутых выражений равно nCV/T, второе–—–Va . Для оставшейся производной можно испробовать преобразование
(¶S/¶V)T ={(6) для F}= (¶p/¶T)V = p’T.
Оно оказалось успешным. Итак‚
ѕ®
.
Здесь второе и третье выражения “опрятнее” первого в том смысле‚ что все коэффициенты во втором члене относятся к одному и тому же набору независимых переменных. Окончательно имеем
или
. (4.8)
K этому результату можно также придти‚ исходя из определений nCp = (¶H/¶T)p, nCV = (¶U/¶T)V, но преобразования будут более громоздкими.
Убедитесь, что для идеального газа (4.8) ведет к соотноше-нию Майера ––Cp–=–CV + R.
Молярные теплоемкости в (4.8) можно заменить на удельные‚ тогда и молярный объем V/n заменится на удельный V/m .
4а. Отношение главных теплоемкостей. Из (4.8) немедленно следует
. (4.9)
5. Соотношение между адиабатическим и изотермическим модулями объемной упругости (или сжимаемостями). В этом случае легче всего получить полезное соотношение для KS/KT
{(3)
в числ.
и знам.}
={(4)
слева и
справа}
‚
откуда
или
. (4.10)
Здесь применен необычный прием–—–вместо поисков пути “улучшения” записанного выражения оно заведомо ухудшено‚ но зато дальше появляется возможность упрощения.
Более естественный путь аналогичен выводу (4.8):
ѕ®
Первое из подчеркнутых выражений равно – (1/V)KT , второе есть p’T. Преобразова-ние последнего множителя по правилу (6) не ведет к немедленному улучшению‚ но
(¶T/¶V)S = {(4)} = – (¶T/¶S)V(¶S/¶V)T = – (T/CV) (¶S/¶V)T
и теперь
(¶S/¶V)T = {(6) для F} = (¶p/¶T)V = p’T . Итак‚
ѕ®
.
Вычисляя отсюда KS/KT и сравнивая с (4.9)‚ получаем (4.10).
6. Изотермическая производная от энергии по объему. Поскольку температура не является естественной независимой переменной для энергии как потенциала‚ следует заменить параметр:
.
Подчеркнутые производные равны соответственно – p и T. Далее‚
(¶S/¶V)T ={(6) для F}= (¶p/¶T)V = Tp’T .
Итак‚
(¶U/¶V)T = – p + Tp’T . (4.11)
Другой метод получения (4.11)–—–выразить U через потeнциал‚ для которого V и T–—– естественные независимые переменные:
U=F+TS;
(¶U/¶V)T = (¶F/¶V)T + T(¶S/¶V)T =
= {(6) для F}= – p+Т(¶p/¶T)V = – p + Tp’T . (4.11а)
Можно также непосредственно использовать основное термодинамическое тождество:
dU= TdS – pdV.
Разделив на dV и наложив условие T = const, имеем
(¶U/¶V)T=T(¶S/¶V)T –p = {(6) для F} = – p +Т(¶p/¶T)V – p є Tp’T – p. (4.11б)
4.7. Внутренняя энергия идеального газа и газа Ван-дер-Ваальса. Важное следствие из (4.11)–—–закон Джоуля: внутренняя энергия идеального газа зависит только от температуры (не зависит от объема): подставляя в (4.11) уравнение состояния‚ находим:
(¶U/¶V)T идеальн. газ = 0. (4.12)
Для газа Ван-дер-Ваальса (p = RT/ (V/n – b) – a/(V/n)2) получаем точно так же:
(¶U/¶V)TВ.-д.-В. = an2/V2, (4.13)
откуда
UВ.-д.-В.=Uидеальн. газ + 
= Uидеальн. газ – an2/V
(4.14)
(поскольку при V ® Ґ газ становится идеальным).
Формула (4.14) позволяет легко получить молекулярное выражение для поправки а в уравнении Ван-дер-Ваальса. Для этого надо учесть‚ что средняя кинетическая энергия всех молекул в любой классической (не квантовой) системе равна внутренней энергии идеального газа. Что касается средней потенциальной энергии‚ то для одной молекулы она равна
,
(4.15)
где r–—–расстояние до соседней молекулы‚ j(r)–—–потенциальная энергия парного взаимодействия‚ n0 = nNAв/V–—–числовая плотность‚ s–—–диаметр жесткого ядра молекулы. Выражение в квадратных скобках имеет смысл полного числа молекул в сферическом слое радиуса r и толщины dr. (В рамках приближений‚ которые принимаются при выводе уравнения Ван-дер-Ваальса‚ нет необходимости учитывать влияние измеменения n0 за счет влияния собственного объема молекул и отклонение средней плотности вблизи молекулы от n0‚ а также отличие s от нуля.) Потенциальная энергия взаимодействия всех молекул найдется умножением (4.15) на nNAв и делением на 2 (чтобы не учитывать дважды каждую пару молекул). Сравнение с (4.14) дает:
a
= (NAв2/2)
. (4.16)
8. Производная изохорной теплоемкости по объему. CV газа Ван-дер-Ваальса. Используя (4.11)‚ получаем
n(¶СV/¶V)T = ¶2U/¶V¶T ={(6)}= ¶2U/¶T¶V=
= (¶(¶U/¶V)T /¶T)V = T(¶2p/¶T2)V . (4.17)
Эту формулу можно получить и без использования (4.11):
n(¶CV/¶V)T = T(¶2S/¶V¶T) ={(6)}= T(¶2S/¶T¶V) (4.17а)
и‚ используя для (¶S/¶V)T правило {(6) для F}, получим (4.17).
Для газа Ван-дер-Ваальса (как и для идеального) подстановка уравнения состояния в (4.17) дает (¶СV/¶V)T = 0 и‚ следовательно‚
СV
= СV
идеальн.
газ
+
=
СV
идеальн.
газ. (4.18)
Для реальных газов этот результат приближенно справедлив только при достаточно больших разрежениях‚ когда уравнениe Ван-дер-Ваальса может служить не только качественной моделью‚ но и количественно удовлетворительным приближением (см.[4]‚ § 4).
9. Дросселирование газа. Измерение теплоемкости разре-женных газов. Эффект Джоуля–—–Томсона. При рассмотрении этих вопросов нам понадобится‚ прежде всего‚ выражение для изотермической производной от энтальпии по давлению:
(¶H/¶p)T = V – Т(¶V/¶T)p = V– TVa. (4.19)
Вывод этой формулы в точности повторяет вывод формулы (4.11) для (¶U/¶V)T с заменой U ® H, V ® p, F ® Ф.
Используя в (4.19) уравнение Клапейрона–—–Менделеева‚ найдем‚ что в идеальном газе энтальпия при постоянной температуре не зависит от давления:
(¶H/¶p)T идеальн. газ = 0 и (¶Cp/¶p)T идеальн. газ = 0. (4.20)
Этот результат следует также из закона Джоуля. Следует учесть‚ что в идеальном газе
(¶U/¶p)T ={(2)}= (¶U/¶V)T(¶V/¶p)T = 0 и (¶[pV]/¶p)T = 0. (4.21)
Дросселированием называется процесс‚ при котором газ перетекает под действием разности давлений p1–––p2 между двумя сосудами (1 и 2) через дроссель — узкое отверстие‚ пористую перегородку или длинную трубку‚ — обеспечивающий достаточно малую скорость течения‚ чтобы состояние газа в сосудах 1 и 2 можно было считать равновесным. Если переместился один моль газа‚ то работа внешних сил по его перемещению равна p1V1–––p2V2‚ где V1–и V2 — значения молярного объема при соответствующих давлениях‚ а приращение его энергии будет
U2–– U1 = p1V1–––p2V2 + Q,
где Q–—–тепло‚ полученное в процессе течения через стенки трубки (ср. 1 ‚§§ 19‚ 24). Отсюда
H2–––H1 = Q. (4.22)
Когда давления p1 и p2 достаточно малы‚ так что газ может cчитаться идеальным по обе стороны дросселя‚ то‚ согласно (4.20)‚ получим
Cp(T2–––T1) = Q . (4.23)
Если соединительная трубка (обычно змеевик) помещена в калориметр‚ то тепло Q можно измерить и‚ таким образом‚ определить Cp. Давления p1 и p2 при этом могут различаться в несколько раз!
В случае неидеального газа представляет интерес изменение температуры при дросселировании в условиях теплоизоляции (эффект Джоуля–—–Томсона). Теперь Q = 0‚ —H2 = H1. При—малом перепаде давлений‚ p2–––p1 = dp (dp < 0), изменение температуры dT = T2–––T1–=–(¶T/¶p)Hdp‚ где
(¶T/¶p)H ={(4)}= – (¶H/¶p)T /(¶H/¶T)p.
Подчеркнутая производная есть Ср. Используя также (4.19)‚ имеем
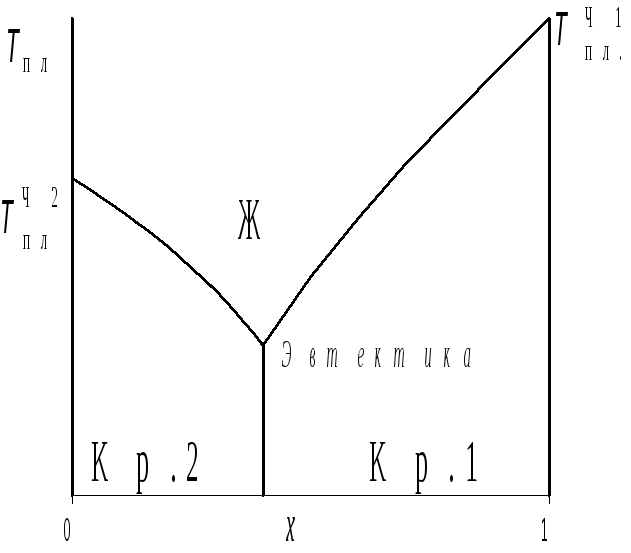={(4)}=
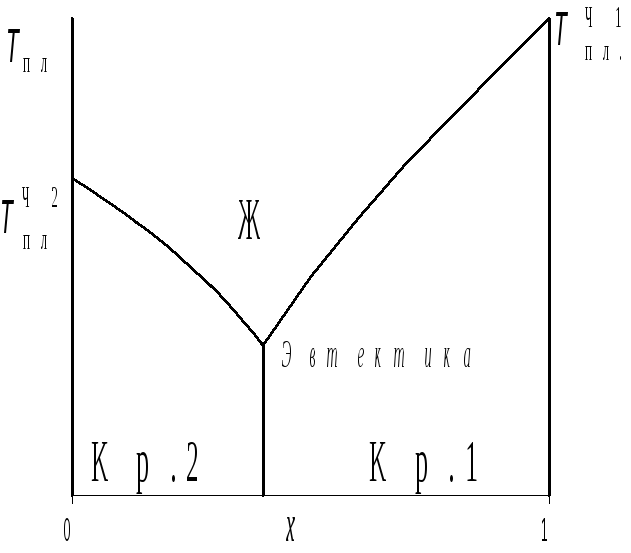. (4.24)
Последняя форма удобна для использования уравнения состояния в форме –p = p(V‚T).– Для идеального газа‚ как легко видеть‚ (¶T/¶p)H = 0.