Глава 8

Тепловые напряжения и тепловых деформации в машинах

Повышенные температуры наблюдаются не только в тепловых машинах, у которых нагрев является следствием рабочих процессов. В «холодных» машинах нагреваются механизмы, работающие при высоких скоростях и больших нагрузках (зубчатые передачи, подшипники, кулачковые механизмы и т. д.). Детали, подверженные циклическим нагрузкам, греются в результате упругого гистерезиса при многократно повторных циклах нагружения-разгружения, а также за счёт выделения тепла в узлах трения (подшипниковые узлы, червячные передачи, …). Повышение температуры сопровождается изменением линейных размеров деталей и может вызвать высокие напряжения.

Если материал при колебаниях температуры лишен возможности свободно расширяться или сжиматься, то в нем возникают тепловые напряжения.

Различают торможение тепловых деформаций детали сопряженными деталями (торможение смежности), которое зачастую возникает при выборке зазоров в узлах и торможение деформаций волокон детали смежными волокнами (торможение формы), которое возникает в самой детали при невозможности изменить геометрические размеры при нагревании или охлаждении.[36]

Торможение смежности. Одним из примеров торможения смежности является соединение деталей, имеющих при работе различную температуру или выполненных из материалов с неодинаковыми коэффициентами линейного расширения.

П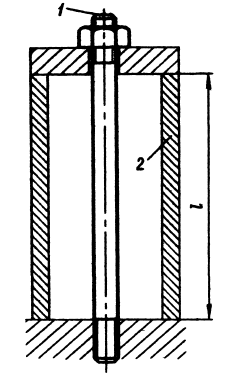 усть болт 1 и втулка 2 (рис. 8.1) изготовлены из материала с коэффициентами линейного расширения а₁ и а₂ и их температуры равны соответственно t₁ и t₂. При нагреве от исходной температуры t₀ болт и втулка в свободном состоянии удлинились бы на величины соответственно la₁∆t₁ и la₂∆t ₂ , где ∆t₁ = t₁ — t₀; ∆t ₂ = t₂ — t₀; l — длина соединения. В стянутой системе образуется температурный натяг

f₁ = la₂∆t ₂ - la₁∆t_1, (8.1)

или в относительных единицах

e₁ = a₂∆t ₂ - a₁∆t_{1 .} (8.2)

В соединении возникает термическая сила Р_T вы­зывающая по закону Гука относительное удлинение болта e₁ = и укорочение втулки , где

и - коэффициенты жесткости соответственно болта и втулки (F₁ и F₂ — сечения болта и втулки). Сумма относительных деформаций . Откуда

. (8.3)

Рис. 8.1. Схема торможения смежности

Примем, что температура стягивающей и стягиваемой деталей оди­накова (как это обычно и бывает в машинах при установившемся тепло­вом режиме). Полагая t_t — t₂ — t, получаем из формул (8.2) и (8.3) . (8.4)

Возможны три случая:

1. а₂ > а₁ (стяжка деталей из алюминиевых, магниевых и медных сплавов стальными болтами и болтами из титановых сплавов). При нагреве в таких соединениях возникает натяг, пропорцио­нальный фактору t (а₂ — а₁). При охлаждении до минусовых температур этот фактор становится отрицательным. Следовательно, первоначальный сборочный натяг уменьшается, т. е. соединение ухудшается.

2. а₁ > а₂ (стяжка стальных и чугунных деталей болтами из аустенитных сталей; стяжка деталей из титановых сплавов стальными болтами). При нагреве фактор t(а₂—а₁) отрицателен, т. е. соединение ухудшается, а при охлаждении до минусовых температур положителен, т. е. перво­начальный натяг увеличивается.

3. а₁ = а₂ (стяжка стальных и чугунных деталей стальными болтами; стяжка деталей из титановых сплавов титановыми болтами). В этом случае

t (а₂ — а₁) = 0, т. е. первоначальный натяг при нагреве и охлаждении не меняется.

Иллюстрация этих закономерностей приведена на рис. 8.2, изобража­ющем изменение температурного натяга t (a₂ — а₁) при стяжке корпусов из различных материалов стальными (8.2, а) и титановыми (8.2, б) бол­тами. Значения а₂ и а₁ взяты из рис. 8.3.

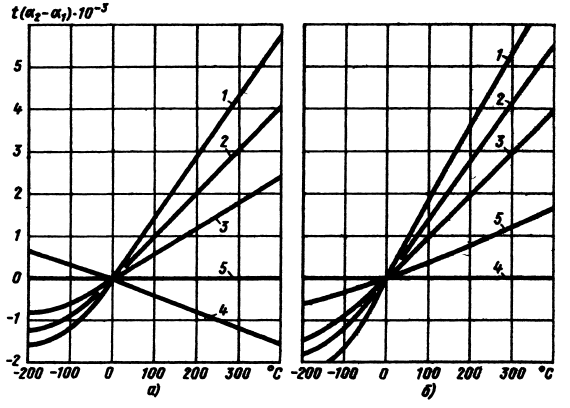
Рис. 8.2

Термический натяг при стяжке корпусов стальными (а) болтами и титановыми (б) болтами.

Материалы корпусов:

1- сплавы Mq,

2- сплавы Аl,

3 – бронзы,

4- сталь и чугун

Согласно формуле (8.3) напряжение растяжения в болте

. (8.5)

Напряжение сжатия во втулке . (8.6)

Отношение . (8.7)

не зависит от модулей упругости материалов шпильки и втулки и опре­деляется только соотношением сечений последних.

На рис. 8.4 приведены подсчитанные по формулам (8.5) и (8.6) напряжения и в функции для стальных шпилек и корпусов из различных материалов (принято е_Т = 1; Е₁ = 1; величины Е₂ выражены в долях от Е₁).

Термические напряжения в шпильках резко падают с увеличением (жесткие шпильки, упругие корпуса). Напряжения в корпусах наоборот возрастают, но при обычных значениях < 1 и для обычных литейных материалов (чугун, легкие сплавы) имеют значительно меньшую величину, чем в шпильках.

На основании графика и формул (8.5), (8.6) можно сделать следующие выводы:

д ля уменьшения термических напряжений в шпильках корпус сле­дует делать упругим, а шпильки - жесткими;

для уменьшения термических напряжений в корпусе шпильки следует выполнять упругими, а корпус - жестким.

Рис. 8.3.

Коэффициент линейного расширения в функции температуры:

1 — сплавы Ti;

2 — стали мартенситного класса;

3 — стали перлитного класса и чугуны;

4 - стали аустенитного класса;

5 - бронзы;

6 - латуни;

7 - сплавы А1;

8 - сплавы Mg

Прочность корпуса обычно не является определяющей для прочности стяжных соединений, поэтому для термически нагруженных соединений целесообразно придерживаться правила: упругий корпус — жесткие шпильки.

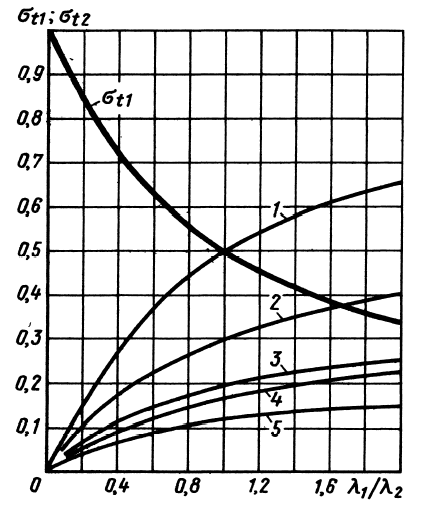
Рис. 8.4.

Относительные термические напряжения (жирная линия)

и (тонкие линии)

в функции .

Материалы корпусов:

1 — сталь;

2 — сплавы Ti;

3 — чугуны;

4 — сплавы А1;

5 - сплавы Mg

Прочность стяжных соединений помимо термических напряжений в значительной степени зависит от силы предварительной затяжки соеди­нения и рабочих сил, действующих на соединение.

Из уравнения (8.3) следует, что возможны следующие способы умень­шения термической силы:

- уменьшение разности температур сопряженных деталей (например, охлаждением стягиваемой детали или увеличением температуры стягива­ющей детали);

- уменьшение разницы в величинах коэффициентов линейного расшире­ния (соответствующим подбором материалов сопряженных деталей).

Если материалы стягивающей и стягиваемой деталей заданы, то тер­мическую силу можно уменьшить введением между стягивающей и стягиваемой деталями промежуточных втулок 1 (рис. 8.5, а), выполненных из материалов с малым коэффициентом линейного расширения, например инвара.

Инвар (36Н) представляет собой железоникелевый сплав (36% Ni, остальное Fe). Коэф­фициент линейного расширения в интервале температур от 0 до 100°С равен

(0 - 1,5) 10 ^-61/°С, резко повышается при t > 200°С . Еще более низким коэффициентом линейного расширения [а= (0 -0,5)*10 ^-6 1/°С в интервале 0-100°С] обладает суперинвар Н30К4Д 32% Ni, 4% Со, 0,7% Си, остальное Fe).

В этом случае температурный натяг f₁ = l₂ a₂ t₂ + l₃ a₃ t₃ – l₁ a₁ t₁, (8.8)

где а₂, а₃, а₁ - коэффициенты линейного расширения соответственно стягиваемых деталей, втулки и шпильки; t₂, t₃, t₁ и l₂, l₃, l₁ — соответственно их температуры и длины.

Вводя l₃ = l₁ – l₂ полагая t₂ = t₃ = t₁ и приравнивая выражение (8.8) нулю, получаем условие отсутствия температурного натяга:

. (8.9)

Подставляя a₂ = 22*10^-6 (алюминиевый сплав), a₃= 1.5*10^-6 (инвар при

20-150 ⁰C) и a₁ = 11 * 10^-6(сталь), находим l₃= 1.15l₂ (8.10)

т. е. для полной ликвидации температурного натяга длина инварной втулки должна превышать на 15% длину стягиваемых деталей. Конструк­тивно это трудно выполнимо.

Е сть материалы, коэффициент линейного расширения которых близок к нулю в широком интервале температур (например, кварц а = 0,55 * 10^-6) и даже имеет отрицательную величину (т. е. размеры детали с нагревом уменьшаются). К таким материалам относятся некоторые ситаллы (а = - 5 * 10 ^-6). Расчет по формуле (8.9) дает в этом случае l₃ = 0,7l₂. Даже при таких условиях промежуточная втулка должна иметь значи­тельную длину.

Для уменьшения термических напряжений стяжные болты иногда выполняют из материалов с высоким коэффициентом линейного расши­рения, например из хромоникелевых аустенитных сталей, для которых a = (14 - 18) * 10 ^-61/°С.

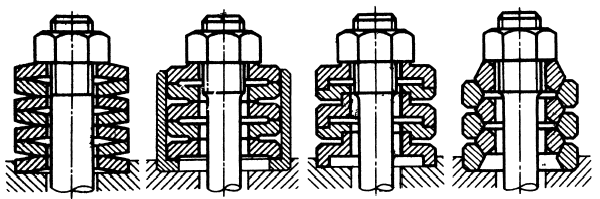
Рис. 8.5. Уменьшение термических напряжений в стяжных соединениях

Действенным средством уменьшения термических напряжений является установка пружинных элементов на корпусах или, что конструктивно удобнее, на болтах (см. рис. 8.5, б). Согласно формуле (8.3) установка пружинных элементов на болтах снижает термическую силу в отношении

, (8.11)

где и — коэффициенты жесткости соответственно болта и стягивае­мых деталей; — коэффициент жесткости болта с упругим элементом

, (8.12)

где — коэффициент жесткости упругого элемента; l_э и l — длины соответственно упругого элемента и болта.

Из формулы (8.11) следует, что термическая сила снижается тем больше, чем выше упругость элемента (чем меньше ).

Если, например, = 0,1 и / = 0,5, то ,

т.е. термическая сила уменьшается в 7 раз. При достаточно большой упругости элемента термические силы могут быть практически полностью погашены.

При ограниченных осевых размерах болт устанавливают в концентрич­ных втулках 2, 3 (см. рис. 8.3, в), из которых первая при затяжке болта работает на сжатие, а вторая — на растяжение. Если сечения болта и втулок равны

(d₂ = ; d₃ = ), то упругость системы повышается приблизительно в 3 раза по сравнению с упругостью собственно болта. Упругие элементы часто применяют для поглощения термических деформаций при установке на валу нескольких деталей, выполненных из сплавов с повышенным коэффициентом линейного расширения (например, роторов многоступенчатых аксиальных компрессоров). Для фиксации и затяжки таких деталей требуется значительная осевая сила. Поэтому упругие элементы в данном случае выполняют в виде набора много­численных прочных и относительно жестких элементов (рис. 8.6), в сумме дающих необходимую упругость.

Рис. 8.6. Упругие элементы в системах силовой затяжки