Глава 7

Контактная прочность

При контактном нагружении сила действует на малом участке поверхности и, как следствие, на поверхностном слое металла возникают высокие локальные напряжения. Этот вид нагружения встре­чается при соприкосновении сферических и цилиндрических тел с плоскими, сферическими или цилиндрическими поверхностями.

При теоретическом решении задачи о напряженном состоянии в зоне контакта упругих тел (Герц, Беляев) предполагают, что нагрузка статическая, материалы тел изотропны, площадка контакта мала по сравнению с поверхностями и действующие усиления направлены нор­мально к этой площадке.

Однозначного решения по точному определению контактных напряжений на настоящее время не существует. Приведем решение, данное Н.М. Беляевым [8] без учёта сил трения на площадке контакта, т.е. для статического нагружения.

Поверхность контакта для случаев, приведенных в табл. 7.2, ограничивается эллипсом, уравнение которого Ax² +By² =C = const; (7.1)

Здесь А и В – величины, зависящие от главных радиусов кривизны каждого из соприкасающихся тел, а С – величина сближения соприкасающихся тел, вызванная упругой деформацией по площадке касания.

Напряжения по площадке соприкасания распределяются по закону эллип­соида и могут быть найдены из уравнения:

, или . (7.2)

Здесь Р— величина давления при касании, — объём полуэл­липсоида напряжений, имеющего в основании эллипс с полуосями а и b, величина которых зависит от отношения A/B.

Величина наибольших напряжений в центре эллипса касания может быть выражена формулой , (7.3)

где а — коэффициент, зависящий от отношения А/В . Значения коэффициента а в функции А/В даны в табл. 7.1.

Таблица 7.1. Значения коэффициента, а в формуле (7.3)

А/В	1,0	0,9	0,8		0,7		0,6		0,5		0,4	0,3
а	0,388	0,400	0,420		0,440		0,468		0.490		0,536	0,600
А/В	0,2	0,15		0,10		0,05		0,02		0,01		0,007
а	0,716	0,800		0,970		1,280		1,800		2,271		3,202

Эллипс контакта обращается в круг при касании двух шаровых поверхностей или шара с плоскостью и в прямоугольник шириной 2b, если перво­начальное касание происходит не в точке, а по прямой (например, при каса­нии цилиндрических катков с параллельными осями).

Таблица 7.2. Формулы определения коэффициентов А, В, и

Продолжение таблицы 7.2.

Материал соприкасающихся тел в центре площадки касания находится в усло­виях объёмного напряжённого состояния и поэтому может работать при очень больших сжимающих напряжениях. Углеродистая сталь, например, может безопасно выдержать напряжения порядка 3500-4000МПа.

Чтобы проверить прочность материала при объёмном напряжённом состоянии, нужно знать величину главных напряжений в опасной точке и составить условие прочности. Можно показать , что опасная точка лежит на некоторой глубине кон­тактирующих тел, и по соответствующим формулам найти главные напря­жения.

Оказывается, что расчётное напряжение в опасной точке внутри мате­риала по энергетической теории прочности . На поверхности соприкасания расчётные напряжения по той же теории прочности соответ­ственно равны:

в центре эллипса касания ,

на конце большой полуоси .

Коэффициенты n₁ и n₂ в функции А/В даны на рис. 7.1

Таким образом, для определения расчётных напряжений, которые сле­дует сравнивать с допускаемыми нормальными напряжениями при про­стом сжатии, надлежит:

1 ) вычислить А и В, принимая за А меньшую из этих двух величин по формулам таблицы 7.2;

2. по отношению А/В найти а (таблица 7.1);

3. вычислить по формуле таблицы 7.2 величину ;

4. для проверки прочности в точках площадки соприкасания умножить на величину коэффициента n (рис. 7.1);

Рисунок 7.1

5) для проверки же прочности в наиболее опасной точке умножить

на 0,60. Величины расчётных напряжений надлежит сравнить с допускае­мыми напряжениями при простом растяжении или с пределом текучести (упру­гости).

Заметим, что на вид фор­мул для контактных напря­жений существенно отли­чается от обычных формул для напряжений при про­стом растяжении или сжа­тии. Раньше, во всех слу­чаях, мы получали вели­чину напряжений прямо пропорциональной величи­не силы и не зависящей от упругих постоянных ма­териала. Из приведённых в табл. 7.2 формул, мы видим, что контактные напряжения зависят от модуля упругости материала и растут медленнее силы .

Пример. Подсчитаем напряжения, возникающие в рельсе с радиу­сом головки г = 300 мм в месте соприкасания с ним переднего колеса тепловоза радиусом R = 470 мм; нагрузка на рельс Р=73000 Н; модуль упругости стали Е=2 * 10⁵ МПа.

Имеем (по таблицам 7.1 и 7.2): ; ; и

Таким образом, ,

расчётное напряжение внутри рельса равно .

На поверхности соприкасания расчётное напряжение равно =0,24*1080=260 МПа.

Здесь п = 0,24 взято по графику (рис. 7.1) средним между значениями п₁ и п₂. На поверхности соприкасания расчётные напряжения близки к пределу текучести, внутри же превышают его; это показывает, что остаточные дефор­мации, правда захватывающие небольшой объём материала, неизбежны в го­ловке рельса.

П.И. Орлов [36] дал решение указанной задачи с учётом сил трения и деформации металла контактирующих тел. Начальный подход в решении задачи одинаков. В зоне соприкосновения образуется площадка, размеры которой зависят от упругости материалов и формы сжимаемых тел. При сжатии сфер (рис. 7.2, а) площадка имеет вид окружности диаметром ,

где Р - нагрузка, Н; Е= - приведенный модуль упругости мa­териалов

сфер, МПа; V = - приведенный диаметр сфер, мм (знак минус относится к случаю соприкосновения выпуклой поверхности с вогну­той поверхностью диаметром D).

При сжатии цилиндров (рис. 7.2, б) площадка имеет вид прямоуголь­ника шириной

Давление максимально в центре площадки в 1,5 раза больше сред­него давления: .

При сжатии цилиндров (рис. 7.3,б) площадка имеет вид прямоугольника

шириной , где V — приведенный диаметр цилиндров, мм; q — нагрузка на единицу длины цилиндров, Н/мм.

Давление максимально по средней линии площадки и в 1,27 раз превышает среднее давление p_max =1.27 q/b.

Волокна материала в зоне действия максимальных давлений находятся в состоянии всестороннего сжатия; в них возникают взаимно перпендикулярные напряжения сжатия и направленные к ним под углом 45° октаэдрические напряжения сдвига 0,5 ( — ); 0,5 ( — ); 0,5 ( — ). Распределение этих напряжений (в долях максимального давления р _max на площадке контакта) по глубине поверхностного слоя (в долях ширины b площадки контакта) показано на рис. 7.3. Нормальные напряжения имеют наибольшую величину ( = = 0,5p_max ; =0,5p_max) на поверхности; касательные напряжения — на расстоянии (0,25 - 0,4) b от поверхности.

В условиях всестороннего сжатия предел текучести закаленных сталей высокой прочности достигает 3000 — 5000 МПа, что примерно в 4 — 5 раз больше предела текучести при одноосном напряжении сжатия. Допускаемые напряжения 1000 — 2500 МПа.

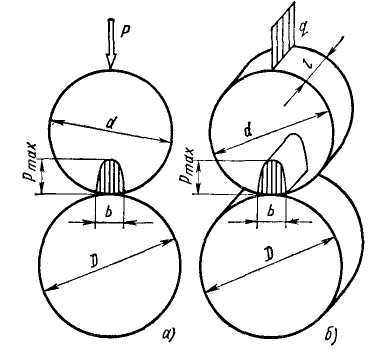
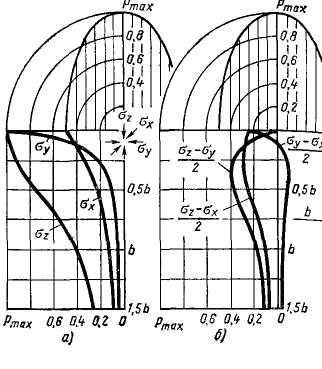Рис. 7.2 Рис. 7.3

В машиностроительных конструкциях нагрузка, как правило, бывает циклической вследствие периодического изменения величины действующей силы, а также вследствие относительного движения соприкасающихся тел.

Основные схемы работы сочленений при контактном нагружении представлены в табл. 7.3 (в скобках приведены конструктивные аналоги)

В схемах 5 — 12 нагружение имеет циклический характер, даже если действующая сила статическая, так как нагружению подвергаются последовательно различные точки поверхностей. Относительное движение кон­тактных тел нарушает распределение напряжений в зоне контакта по Герцу. Поверхностный слой в зоне контакта подвергается сжатию и растяжению в тангенциальном направлении. Расположение зон сжатия и растяжения зависит от кинематики движения. При чистом качении (схемы 7—9) зоны сжатия на обеих сопрягающихся поверхностях (зачерненные участки) рас­положены по одну сторону от центра контакта (встречно движению), по другую сторону материал подвергается растяжению.

При скольжении (схема 10) и качении со скольжением (схемы 11, 12) участок сжатия на опережающей поверхности (рис. 7.4, а) расположен перед центром контакта (встречно движению), а на отстающей поверх­ности — наоборот; на противоположных участках материал подвергается растяжению (рис.7.4, б).

В зоне сжатия опережающей поверхности (рис. 7.4, в) происходит сближение и сдвиг волокон материала в направлении, указанном стрел­ками. В зоне растяжения волокна, упруго расправляясь, перемещаются в том же направлении. На отстающей поверхности волокна перемещаются в обратном направлении. В результате на поверхности контакта возникают силы трения, отклоняющие действующие силы от нормали к площадке контакта.

Таблица 7.3. Основные виды контактного нагружения

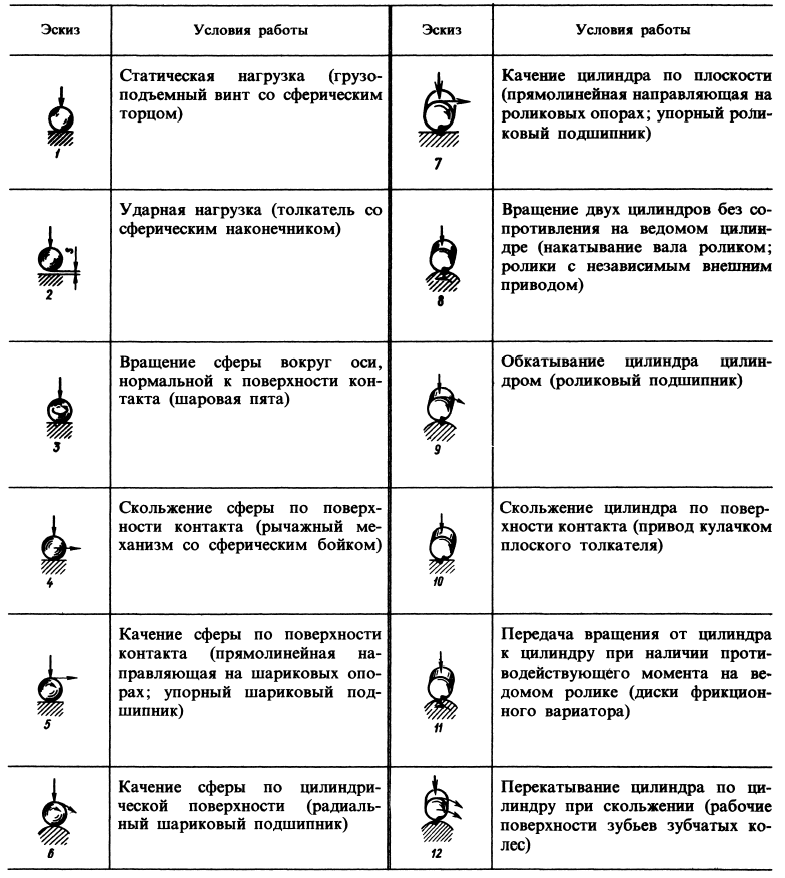
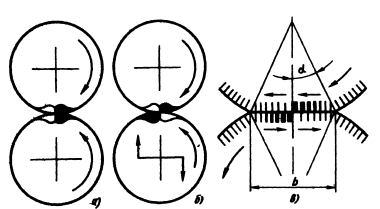
Рис. 7.4

Сжатие и растяжение в зоне контакта.

Периодическое сжатие и растяжение волокон вызывает, кроме того, систематическое отставание ведомого тела. Длина поверхности ведущего тела на угле контакта а равна 0,5b -∆b, где ∆b — упругое укорочение поверхности. Длина поверхности ведомого тела на том же участке равна 0,5b + ∆b', где ∆b' — упругое удлинение поверхности. Следовательно, ско­рость вращения ведомого тела меньше скорости ведущего тела в отно­шении

i=(0,5b -∆b):( 0,5b + ∆b') =(1-2∆b/b):(1+2∆b/b).

Практически i = 0,99 0,995.

Из предыдущего ясно, что действительные условия в зоне контакта гораздо сложнее, чем при статическом нагружении, вследствие чего фор­мулы, выведенные для случая статического нагружения, применимы только как первое приближение.

Долговечность циклически нагруженных соединений определяется уста­лостной прочностью материала. Кривые усталостной прочности при статическом нагружении, вследствие чего фор­мулы, выведенные для случая статического нагружения, применимы только как первое приближение.

Д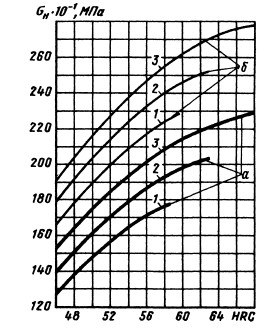 олговечность циклически нагруженных соединений определяется уста­лостной прочностью материала. Кривые усталостной прочности при контактном нагружении в общем близки к кривым усталости для случаев одноосного напряженного состояния (растя­жения, сжатия) с тем различием, что числен­ные значения разрушающих напряжений го­раздо выше и кривые не имеют отчетливо выраженного горизонтального участка пре­дела выносливости.

Главное значение для усталостной прочно­сти в условиях контактного нагружения имеет твердость поверхностного слоя (рис. 7.5).

Рис. 7.5

Циклическая контактная прочность

в функции НRC:

1 - сталь 45ХН (обработка ТВЧ);

2 - сталь 20Х2Н4А (цементация);

3 - сталь ШХ15 (закалка и низкий отпуск):

а) - предельные напряжения при N = 10⁷ циклов;

б) -при N = 10⁸ циклов

Про­цесс усталостного разрушения при контактном нагружении протекает по-особому. Первичные трещины зарождаются в зоне действия максимальных касательных напряжений на глубине, равной 0,3-0,4 размера площадки контакта. Постепенно развиваясь, они выходят на поверхность, образуя характерную точечную сыпь. На даль­нейшем этапе точечные дефекты разрастаются и сливаются в цепочки; на участках между цепочками отслаиваются и выкрашиваются крупные частицы металла. Это явление называется питтингом. В результате питтинга сочленение, как правило, выходит из строя.

Повышение скорости относительного движения (качение с проскальзы­ванием) оказывает до известной степени благоприятное влияние. Повреж­денный слой в процессе износа постепенно удаляется, вследствие чего выкрашивание не возникает. Долговечность сочленения здесь зависит от интенсивности абразивного износа, изменяющего с течением времени первоначальную форму контактных поверхностей.

Типичным примером контактного усталостного разрушения является питтинг рабочих поверхностей зубьев колес. Питтинг сосредоточивается на участках зуба, близких к начальной окружности. Это объясняется тем, что при обычных значениях коэффициента перекрытия ( = 1,2 -1,8) на этих участках нагрузку несет один зуб, а на участках, близких к головке и ножке, — два. Кроме того, на средних участках профиля происходит перекатывание без скольжения, тогда как на участках у головки и корня имеет место также проскальзывание. Эти участки подвергаются шлифу­ющему действию сопряженных поверхностей, удаляющему поверхностные повреждения, но со временем приводящему к искажению эвольвентного профиля.

Присутствие смазки действует двояко. При умеренных давлениях в зоне контакта масляная пленка способствует более равномерному рас­пределению давлений и увеличению фактической поверхности контакта. Перекатывание поверхностей создает определенный гидродинамический эффект: в пленке, вытесняемой из зазора, возникают повышенные давления, способствующие разделению металлических поверхностей, тем более, что при давлениях, существующих в зоне контакта, увеличивается вязкость масла. В результате нагрузка воспри­нимается отчасти упругой деформацией выступающих металлических поверхностей, отчасти давлением в масляной пленке (эластогидродинамическое трение).

Еще резче выражен гидродинамический эффект при скольжении. Масло, увлекаемое движущейся поверхностью, непрерывно поступает в сужива­ющуюся часть зазора, разделяя металлические поверхности. При благо­приятных соотношениях (большие скорости скольжения, малые давления, повышенная вязкость масла) в сочленении наступает жидкостное трение.

При высоких давлениях в зоне контакта масло оказывает отрицатель­ное влияние. Под действием набегающей поверхности, а также вследствие капиллярности, масло внедряется в рыхлоты и микротрещины и расши­ряет их, вызывая ускоренное выкрашивание металла. Особенно резко это явление выражено в случае, если одна из поверхностей в зоне повышен­ного давления подвергается растяжению (см. рис. 7.4, в), способствую­щему раскрытию микротрещин.

Задача повышения прочности контактных сочленений заключается прежде всего в снижении величины давлений на площадке контакта путем придания рациональной формы сопрягающимся поверхностям.