Поведение модели - групповой образ жизни хищников и их жертв радикально меняет поведение модели, придает ей повышенную устойчивость.

Обоснование: при групповом образе жизни снижается частота случайных встреч хищников с потенциальными жертвами, что подтверждается наблюдениями за динамикой численности львов и антилоп гну в парке Серенгети.

5

Постановка задачи:

допустим у нас есть закрытый ареал, существа которого не иммигрируют и не эмигрируют. Также допустим, что еды для травоядных животных у нас имеется с избытком. Тогда уравнение изменения количества жертв примет вид:

где:

•  — это коэффициент рождаемости жертв

•  — это величина популяции жертв

•  — это скорость прироста популяции жертв.

Так как хищники стабильным питанием не обеспечены, то они вымирают. Следовательно уравнение для хищников примет вид:

где:

•  — это коэффициент убыли хищников

•  — это величина популяции хищников

•  — это скорость прироста популяции хищников.

Встречи хищников и жертв (которые ), убивают жертв с коэффициентом и рождают новых хищников с коэффициентом . С учётом этого, получаем систему уравнений:

6

Решение задачи:

Нахождение стационарной позиции системы.

Найдем стационарную точку , , вокруг которой происходят колебания. Для стационарной позиции изменение популяции равно нулю. Следовательно:

Из чего следует, что:

Задание отклонения системе:

теперь нам надо ввести в нашу систему колебания и . Из-за малой величины квадратами, кубами и т.д. можно пренебречь. Теперь популяция и будет равняться:

Далее расписываем предыдущее уравнение:

Похожий ответ получаем относительно хищников:

После чего дифференцируем одно уравнение и подставляем в него другое:

7

— является уравнением гармонического осциллятора с периодом

Рассмотрим модель взаимодействия хищников и их добычи, когда между особями одного вида нет соперничества. Пусть x₁ и x₂ — число жертв и хищников соответственно. Предположим, что относительный прирост жертв x₁'/x₁ равен a-bx₂, a>0, b>0, где a — скорость размножения жертв в отсутствие хищников, -bx₂ — потери от хищников. Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи ( x₁=0 ) относительная скорость изменения популяции хищников равна , c>0 , наличие пищи компенсирует убывание, и при x1>0 имеем , d>0. Таким образом, система Вольтерра—Лотка имеет вид:

где a, b, c, d>0

Рассмотренная модель может описывать поведение конкурирующих фирм,рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и пр. Рассмотрим фазовый портрет системы Вольтерра—Лотка для a=4, b=2.5, c=2, d=1 и графики ее решения с начальным условием x₁(0)=3, x₂(0)=1, построенные программой ОДУ.

 

 

8

Видно, что процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов 3: 1 , обе популяции сначала растут. Когда число хищников достигает величины b=2.5 , популяция жертв не успевает восстанавливаться и число жертв начинает убывать. Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников и когда число жертв достигает величины x₁=c/d =2 (в этой точке x₂'=0), число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор,

9

пока число хищников не достигнет величины x₂=a/b =1.6 (в этой точке x₁'=0).С этого момента начинает расти популяция жертв, через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и процесс повторяется снова и снова. На графике четко виден периодический характер процесса. Количество жертв и хищников колеблется возле величин x₁=2, x₂=1.6 соответственно (дробные числа здесь не означают “половину волка”, величины могут измеряться в сотнях, тысячах и т.п.). Периодичность процесса явственно видна на фазовой плоскости— (x₁(t), x₂(t)) — замкнутая линия. Самая левая точка, этой кривой, - это точка, в которой число жертв достигает наименьшего значения. Самая правая точка x₁=4, x₂=1.6 , — точка пика популяции жертв. Между этими точками количество хищников сначала убывает, до нижней точки фазовой кривой,x₁=2 , где достигает наименьшего значения, а затем растет до верхней точки фазовой кривой (x₁=2, x₂=2.5). Фазовая кривая охватывает точку x₁=2, x₂=1.6. На языке дифференциальных уравнений это означает, что система имеет стационарное состояние x₁' =0, x₂' =0, которое достигается в точке x₁=2, x₂=1.6. Если в начальный момент система находилась в стационарной точке, то решения x₁(t), x₂(t) не будут изменяться во времени, останутся постоянными. Всякое же другое начальное состояние приводит к периодическому колебанию решений. Неэллиптичность формы траектории, охватывающей центр, отражает негармонический характер колебаний.

Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и т.п.

 

10

Пример 1. Динамика популяций.

  Уравнения Вольтерра-Лотка с логистической поправкой.

Рассмотрим модель конкурирующих видов с “логистической поправкой”:

В этом случае поведение решений в окрестности стационарной точки меняется в зависимости от величины и знака параметра a. Рассмотрим фазовый портрет системы Вольтерра—Лотка для  a =0.1, a=4, b=2.5, c=2, d=1 и графики ее решения с начальным условием x₁(0)=3, x₂(0)=1, построенные программой ОДУ.

 

 

11 

Видно, что в этом случае стационарная точка превращается в устойчивый фокус, а решения — в затухающие колебания. При любом начальном условии состояние системы через некоторое время становится близким к стационарному и стремится к нему при .

Графики решений и фазовая кривая при отрицательном значении параметра a, a =-0.1, приведены ниже.

 

 

 Как видно, в этом случае стационарная точка является неустойчивым фокусом и амплитуда колебаний численности видов растет. В этом случае как бы близко ни было начальное состояние к стационарному, с течением времени состояние системы будет сильно отличаться от стационарного.

12

Пример1

Определим номер первой компоненты вектора равным 1 (а не 0, как положено по умолчанию)

Построим график решения и соответствующую фазовую кривую. Для этого решим задачу Коши методом Рунге-Кутты, воспользуемся функцией rkfixed

Определим правую часть системы D(t,Y)

Для того чтобы ввести правые части системы в векторной форме, щелкните по символу матрицы в панели Matrix, определите в окне размерности число строк (2) и число столбцов (1), а затем введите в помеченных позициях выражения для вычисления правых частей.

Вычислим приближенное решение, выполнив методом Рунге-Кутты 4-го порядка 100 одинаковых шагов; обозначим приближенное решение Y

В первом столбце матрицы Y хранятся значения значения t в узлах сетки, во втором столбце - соответствующие значения решения, в третьем - значения производной решения.

13

Для того чтобы построить фазовую кривую, щелкнем в панели Graph по пиктограмме двумерного декартова графика (X-Y Plot) и введем в помеченной позиции возле оси абсцисс имя второго столбца, а возле оси ординат - имя третьего столбца матрицы, содержащей приближенное решение. Для того чтобы ввести номер столбца, щелкнем по символу столбца в панели Matrix и введем номер столбца в помеченной позиции в угловых скобках.

Для того чтобы построить график решения, щелкнем в панели Graph по пиктограмме двумерного декартова графика (X-Y Plot) и введем в помеченной позиции возле оси абсцисс имя первого столбца, а возле оси ординат - имена второго и третьего столбцов матрицы, содержащей приближенное решение

14

Модель Холлинга-Тэннера

Еще одна нелинейная модель системы «хищник-жертва» была предложена Холлингом и Тэннером (рис. 4.24). Эта модель имеет две важные особенности. Ее нелинейность довольно сильна, что видно из вида фазового портрета, витки которого заметно отличны от эллипсов. рис. 4.24. Моделирование системы «хищник-жертва» Холлинга - Тэннера

Главное свойство этой модели заключается в том, что в конечном счете колебания задаются предельным циклом фазового портрета, который может быть устойчивым. Он и определяет амплитуду колебаний, которые устанавливаются в стационарном режиме работы системы. При этом

15

колебания могут как затухать во времени (пример чего и приведен), так и возрастать, приближаясь при этом к стационарным колебаниям.

Моделирование замкнутой экономической системы - в поведении биологических и экономических систем есть много общего. Поэтому при обсуждении моделей экономических систем ограничимся описанием модели замкнутой практически линейной экономической системы, которая описывается дифференциальным уравнением второго порядка (рис. 4.25). Эта модель характеризуется двумя параметрами - круговой и параметром затухания k. Поведение системычастотой осцилляций существенно зависит как от этих параметров, так и от начальных условий.

Так, оно может иметь как апериодический, так и колебательный характер.

рис. 4.25. Моделирование замкнутой экономической системы

16

На примере модели Вольтерра—Лотка и модели Вольтерра—Лотка с логистической поправкой было продемонстрировано одно из важнейших качественных свойств центров — они легко разрушаются даже при самых малых изменениях правой части. Большинство моделей является идеализацией действительности; в них внимание сосредоточено на некоторых основных переменных и соотношениях между ними. Поэтому устойчивость моделей относительно малых возмущений чрезвычайно важна в приложениях. Модели, не чувствительные к малым возмущениям, называются грубыми.

Модель Вольтерра—Лотка неустойчива относительно возмущений, поскольку ее стационарное состояние — центр. Существует другой вид моделей, в которых возникают незатухающие колебания — это модели, имеющие на фазовых портретах предельные циклы. Такая модель существует для системы конкурирующих видов — это модель Холлинга - Тэннера Скорость роста популяции жертв x'₁ в этой модели равна сумме трех величин:

• скорости размножения в отсутствие хищников — r x₁;

• влиянию межвидовой конкуренции за пищу при ограниченных ресурсах (для случая конкурирующих производителей это влияние ограниченных сырьевых ресурсов) —

• влиянию хищников , в предположении, что хищник перестает убивать, когда насыщается —

Скорость роста популяции хищников x'₂ строится так же, как в модели Вольтерра—Лотка, в предположении, что жертвы встречаются редко. Если для поддержания жизни одного хищника нужно J жертв, то популяция из x₁

17

жертв сможет обеспечить пищей x₁/J хищников. Модель роста популяции хищников, в которой их число не может превысить эту критическую величину, имеет вид: Таким образом, имеем модель Холлинга—Тэннера:

где r, s, K, D, J > 0.

Можно показать, что при на фазовом портрете системы будет устойчивый предельный цикл. Ниже приведено решение системы при r=1, K=7, w=1, D=1, s=0.2, J=0.5 и двух различных начальных состояниях и фазовый портрет системы, построенные программой ОДУ.

 

 

18

 

19

Выравнивание цен

Модель выравнивания цен по уровню актива интересна тем, что в ней можно наблюдать гармонические колебания решений возле стационарного состояния. Предположим, что изменение уровня актива q пропорционально разности между предложением s и спросом d, т.е. q'=k(s-d),  k > 0. Предположим далее, что изменение цены p пропорционально отклонению актива q от некоторого фиксированного уровня q₀ так, что p'=-m(q-q₀ ) , m > 0. Таким образом, модель выравнивания цен по уровню актива имеет вид q'=k(s(p)-d(p)), p' = - m(q-q₀). Ниже приведены график решения и фазовая кривая для s(p)=ap+s₀, d(p)=cp+d₀, k=0.3, m=0.1, q₀ =20, a=20, s₀ =10, d₀ =50, c=-10 при начальном состоянии q(0)=19, p(0)=2 построенной программой ОДУ.

 

 

20

 

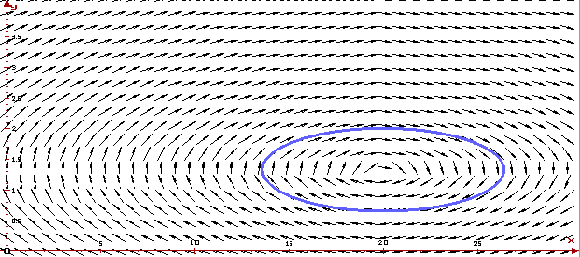
Видно, что цена и актив колеблются возле стационарного состояния. Фазовая траектория представляет собой эллипс, охватывающий стационарную точку. Это означает, что колебания актива и цены — гармонические.

Пример 1.

  Определим номер первой компоненты вектора равным 1 (а не 0, как положено по умолчанию)

Такая запись приведена только для удобства восприятия. Условия задачи будут записаны ниже.

21

Построим график решения и соответствующую фазовую кривую. Для этого решим задачу Коши методом Рунге-Кутты, воспользуемся функцией rkfixed

Определим правую часть системы D(t,Y)

, , , , , ,

Вычислим приближенное решение, выполнив методом Рунге-Кутты 4-го порядка 100 одинаковых шагов; обозначим приближенное решение Y.

Для того чтобы ввести правые части системы в векторной форме, щелкнем по символу матрицы в панели Matrix, определим в окне размерности число строк (2) и число столбцов (1), а затем введем в помеченных позициях выражения для вычисления правых частей.

В первом столбце матрицы Y хранятся значения t в узлах сетки, во втором столбце - соответствующие значения решения, в третьем - значения производной решения

22

Для того чтобы построить фазовую кривую, щелкнем в панели Graph по пиктограмме двумерного декартова графика (X-Y Plot) и введем в помеченной позиции возле оси абсцисс имя второго столбца, а возле оси ординат - имя третьего столбца матрицы, содержащей приближенное решение. Для того чтобы ввести номер столбца, щелкнем по символу столбца в панели Matrix и введем номер столбца в помеченной позиции в угловых скобках.

23

Заключение

Данная работа посвящена развитию методик параметрического моделирования динамики популяций, и применению полученных результатов в актуальных прикладных исследованиях. Моделирование систем на основе анализа влияния эндогенных и экзогенных статистических показателей на параметры функциональных зависимостей является одним из перспективных путей решения теоретических и прикладных задач в этой области. В настоящее время благодаря усилиям многих исследователей в значительной мере разработана методология математического моделирования и достигнуты большие успехи в применении таких моделей в прикладных разработках. Также в работе проведена систематизация и предпринята попытка развития параметрических методов моделирования динамики численности популяций, вводится понятие "информационного параметра" как отличительной черты цивилизованного общества от биологической популяции.

Одним из направлений данной работы было исследование влияния неоднородности популяции по какому-либо признаку на динамику её численности. Обычно при построении соответствующих моделей исследователи обычно делают предположения об однородности популяции по различным биологическим, а для населения - также по социальным, экономическим признакам и об однородности влияния внешней среды на процессы рождаемости и смертности. Это, как правило, не соответствует реальности и дает расхождение между моделируемыми и наблюдаемыми величинами. В данной работе приводятся некоторые результаты моделирования популяции со стабильной возрастной структурой, неоднородной по некоторому биологическому или социальному признаку.

24

Список используемой литературы

1. Радченко, М. Г. 1С: Предприятие 8.0. Практическое пособие разработчика. Примеры и типовые приемы [Текст] / М. Г. Радченко. - М.: ООО "1С-Паблишинг", 2004. - 331 с.

2.А.С.Гринберг, Н.Н. Гобачев, А.С.Бондаренко Информационные технологии управления Изд-во: Альпина Бизнес Букс, 2004.

3. Интернет ресурс www.buhpro.com внедренческий центр: бухгалтерские программы.

4. Симонович С.В. « Информатика базовый курс».

5. Дьяконов В. « Mathcad 2000».

6. Плис А.И. Сливина Н.А. «Mathcad 2000 математический практикум»

7.  Симонович С.В Информатика. Базовый курс.2- е издание — СПб.: Издательство «Питер», 2005- 640 с.

8. Макаров Е.Г. Инженерные расчеты в MathCAD. Учебный курс.- СПб.: Издательство «Питер», 2005.- 448 с.

9. http://www.ascon.kiev.ua/cgi-bin/view.pl?/CAE/WinMachine/About/About

10. http://www.cadacademy.ru/courses/software/detail.php?ID=1075

11.http://www.centerit.net/staff/CAD_CAE_CAM/Stati/Stati_ob_APM_WinMachine/NovievazmojnostiproektaM%20Win.htm