31.Элементарные задачи на построение с помощью циркуля и линейки

Геометр построение подразумев умения выполнять как минимум 2 вида учебных заданий:1строить (изобр) фигуры на плоскости,2 решать задачи на построен неизвестной искомой фигуры для которой даны в качестве известных только некот элемен.

Очевидно что каждая из этих направ иммет свою специфику, если в первом случае достаточно знать определение и вид изображаемой фигуры, а так же харак свойства , то изображение фигур строится без допол обоснован и доказ.сущест ряд требов к изобр фигур на плоскости если чептеж связан с условиепм задачи,то его обычно располог с левого края доски или страниц тетради, все основ линии чертежа должны иметь большую толчину чем вспомогает линии. Фигуры и их элементы обоз буквами латин и гречес алфавита, все чертежи в тетради ученика дол быть выполнены простым карандашом с примен чертеж и измерит приборов исключ состав наброски к чертежам можно выпол от руки, обозначен делаются ручкой.при изобр фигур допустимо исполь чертеж треуголь для пример построения прямых и углов 30, 60, 45.

При построен искомой фигуры по ее элементам существенно меняются требован использов чертеж инструм и их колич,часто эти требов привод в формул задачи.

Пр С помощью одного чертежного треуг найдите центр данной окруж утраченной во время ее построения. .если в услов построении не указан вид и колич инструм, то подразумев что она решается с помощью циркуля и линейки. Элементарные задачи на построение с помощью циркуля и линейки которые используются при построен более сложных задач.

1.разделить данный отрезок на 2 равные части пополам

1.w1(A,R>AB/2), 2.W2(B,R), 3.W1∩W2={C,D}, O-серед AB

2.востановить перпенд к данной прямой в данной на ней точке

1сп 1AM=MB, 2.W1(A,R>=AM), 3.W2(B,R), 4.W1∩W2=P, 5.PM-иском перпен

2сп 1.O¢a, 2.W(O,ON), 3.W∩a=M, 4.MO∩W=K,KM-ДИАМ, 5.NK-иском перпен

3.Опустить перпенди на данную прямую из точки не лежащей на дан прям

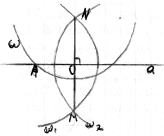1.w(N,R>p(N,a)) 2.W∩a={A,B} 3. W2(A,AN),4. W2(B,BN), 5. W1∩W2=M, 6.NM,NO- иском перпен

4.Через данную прямую и т не лежащую на ней, провести прямую пар данной прям

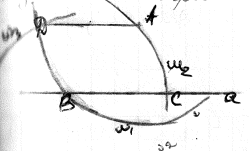1.w1(a, R>p(A,a))) 2.W1∩a=B 3.W2(B,R) 4.W2∩a=C 5.W3(B,AC) 6.W3(B,AC) 7.OA//a

5.Раздел дан отрез на части пропор числам 1:2:3

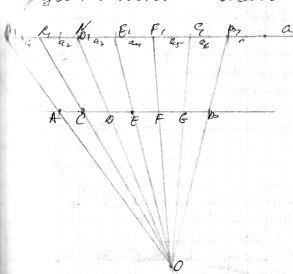1.N¢AB 2.a//AB,N€a 3.a1=a2=..a6 4.AA1∩BB1=0 5.C1∩AB=C, E1∩AB=E,

D1∩AB=D, F1∩AB=F, G1∩AB=G, 6.AC:CE:EB=1:2:3

6. Построить угол равный данному с вершиной в данной точке

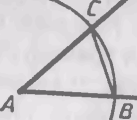
1.OM 2.W(A,R) 3.W∩AB=B 4.W∩AC=C 5.W(O,R) 6.W1∩OM=D 7.W2(D,BC) 8.W1∩W2=E 9.OE 10.<CAB=<EOD

7.Построить биссек дан угда

1.W(A,R) 2.W∩AB=B 3.W∩AC=C 4.W1(B,R) 5.W2(C,R) 6. W1∩W2=E 7.AE-биссек

3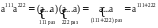 2. понятие числа в школьном курсе мат-ки. Натуральные числа в курсе мат-ки 5-6 классов. Понятие числа яв-ся стержневым понятием школьного курса мат-ки и служет также фундаментом, на котором строится изучение функции, тождественных преобразовании, уравнений и т.п. Понятие числа относится к основным понятиям мат-ки. Поэтому учение о числе яв-ся одним из главных вопросов курса мат-ки средней школы. Современная мат-ка имеет дело с различными по природе числами : натуральными, с целыми, с рациональными, с действительными, с комплексными, с гиперкомплексными. Числа и операций над нами изучаются в таких мат-ких дисциплинах как алгебра и теория чисел. Основное положение, связанные с развитием у учащихся представления о числе, отнесены к курсу мат-ки 4-5 классов (введение дробных и отрицательных чисел), что находится в соответствии с местом этого вопроса в фундаментальных разделах мат-ки. Проводя в школьном курсе мат-ки линию развития понятия числа, учитель придерживается принципа расширения множества А до множества В, определяемого следующими условиями: 1. А должен быть подмножеством В. 2. Операции над элементами из множества А те же, что и для элементов из множества В, но смысл тех операции, которые были только во множестве А, остается неизвестным. 3. Во множестве В должно быть выполнена операция, которая во множестве А была не выполнима или не всегда выполнима. 4. Расширение В должно быть минимальным из всех расширении множества А и должно определяться однозначно с точностью до изоморфизма. Два множества называются изоморфными относительно какой-либо операции, если между их элементами можно установить взаимно однозначное соответствие таким образом, что это соответствие распространяется и на результаты операции. Преподавание вопросов связанных с развитием учения о числе, учитель строит таким образом, чтобы ясно было связь понятий равенства, суммы и произведения с одной стороны, и понятия числа с другой стороны. Нет понятия равенства, суммы, произведения без понятия числа, но нет также понятия числа без понятия равенства, суммы, произведения. Числа обладают свойствами, которые мы выражаем в понятиях равенства, суммы и произведения. Для построение арифметики натуральных чисел используется чисел используется обычно аксиоматический подход. Учителю мат-ки известно и другие построения арифметики натуральных чисел, связанных с именем кантора, основанное на теории множеств и, в частности, на понятии мощности любого множества. В школьном курсе мат-ки изучение арифметики натуральных чисел основано прежде всего на наглядности. Однако основой изложения этого материала в учебниках и на уроках яв-ся ясное и последовательное логическое строение его. Причем обучение арифметике натуральных чисел исходит из самостоятельного происхождения этих чисел из счета предметов. Формальное понятие натурального числа начинается в начальной школе. В IV классах проводится систематизация и расширение сведении о натуральном числе, полученный в начальной школе. Изучение натуральных чисел здесь связано с формирование таких важных для мат-ки понятии, как «координатный луч», «уравнения» и «неравенства». Важно обратить особое внимание, ибо это готовит к пониманию необходимости введения новых чисел, т.е. к расширению понятия числа. Выясняется такое св-во множество натуральных чисел, как бесконечность. С помощью координатного луча сравниваются натуральные числа между собой, устанавливается понятия «равно», «больше», «меньше» для натуральных чисел.

34.

Различают системат и эпизодич виды и формы организ внекл занятий к системат относят математ кружок, мат науч общество учащ, мат лекторий, переодич мат печать. Особое место занимают мат олимпиад. Хотя их проведение является разовым(1 раз в год) но подготовка к ним обычно проводится системат в течении всего года в виде фрагментов занятия кружка мат и разнообразных тренингов.

С меньшей переодич подчас эпизодический провод различ матем соревнов , конкурсы, турниры, викторины.довоьно часто по форме такие мероприят являют аналог известных телевизионных игр или шоу. Одной из форм орган внекл раб в этом направ является провед в школе мат недель, декатников, месячников. В программу этих мероприят по специально состав плану включают «5минутка» с интересными фактами по матем и ее истории во время уроков, беседы на разичные матем темы внутри каждого класса, конкурсы и турниры между классами, 2 тура матем олимпиад, конкурс мат газет и журналов и обще школьный матем вечер.

Матеем кружок- одна из наиболее действенный и эффектив форм внекл зад. В основе кружковой раб лежит принцип строгой добровольности.Обычно кружки организуются для хорошо успевающ иногда и слабо успевающ изъявляют желание участвовать в работе кружка и не редко весьма успешно, учителю не следует этому препятствовать, необходимо лишь более внимательно отнестись к таким учащимся.Уже при организации матем кружка необход заинтересовать учащихся, показать им что рпабота в кружке не является дублированием классных занятий, четко сформулировать цели и раскрыть характер предстоящей работы.на первом занятии надо наметить основное содержание работы ,выбрать старосту , договориться с учащимися о правах и обязанностях члена кражка, составить план работы и распределить поручения за те или иные мероприятия.. Занятия кружка надо целесообразно проводить 1 раз в неделю.к организации работы мат кр целесообразно привлекать самих учащихся.

35.4-угольники—традиционный для курса планиметрии ма­териал. Как и треугольник, четырехугольник трактуется в одних учебниках как простая замкнутая четырехзвенная ломаная, в дру­гих — как часть плоскости, ограниченная такой ломаной. Из все­возможных четырехугольников выделяются выпуклые. Во всех пособиях осуществляется одинако­вый подход во введении частных видов параллелограммов: прямо­угольников и ромбов. Квадрат в одних учебниках вводится как четырехугольник, к-рый одновременно яв/ся прямоугольни­ком и ромбом. В других квадрат определяется как частный вид прямоугольника. Трапеция рассматривается после параллело­граммов.

При установлении различных свойств и признаков параллело­грамма широко используются свойства и признаки равных тре­уг-ков, свойства углов, образованных при пересечении двух параллельных прямых третьей, признаки параллельности прямых. Материал о параллелограммах и их частных видах очень удобен для формирования и развития логического мышления учащихся.

В настоящее время широкое распространение получают уроки общения, общественные смотры знаний и др. При этом учебный1

процесс активизируется, ученики осваивают новые приемы учебной работы, их знания по определенному разделу систематизируются, обобщаются. Воспитывается чувство коллективизма, ответственности за товарища, умение заметить хорошее и найти недостатки в ответе другого ученика.

Успешно проходят в школах общественные смотры знаний по теме «Четырехугольники». За 2; 2,5 недели до его проведения учащимся сообщается перечень вопросов по теме, список задач. Учитель называет консультантов и их группы. Консультанты готовят членов своей группы к обще­ственному смотру знаний, проходит на уроке геометрии. Класс подготовлен к его проведению; на стенах развешены готовые чертежи к каждой из предложенных задач; в классе имеются часы; столы, за которыми сидят консультанты. У каждого консультанта на столе имеются: опросный лист с II колонками для оценок стопочки карточек разного цвета и список теоретических вопросов. Учитель объявляет начало общественного смотра знаний и назначает, кто к кому пойдет отвечать. Отвечающий должен иметь при себе творче­скую работу по теме «Четырехугольники» и тетрадь с решением всех задач по теме. Учитель руководит работой остальных учеников. Они могут выполнять контрольную работу по теме из «Дидактиче­ских материалов». Отвечающий вытаскивает 5 разноцветных карто­чек с задачами. Консультант задает последовательно 5 вопросов по теории и оценивает каждый ответ. После этого отвечающий берет одну из задач, находит соответствующий чертеж и по нему объясняет решение задачи. Каждое решение оценивается спрашивающим.

В конце урока каждый из консультантов комментирует ответ -тех, кого он опрашивал. Общий итог подводит учитель.

Свойства и признаки четырехугольников разных видов находят широкое применение при изучении многогранников и тел вращения. Свойство площадей подобных многоугольников применяется при рассмотрении сечения пирамиды плоскостью, параллельной осно­ванию.