Решение.

Подозрение вызывают только точки, в которых функция меняет свое аналитическое выражение: х₁=0, х₂=1. Проверим функцию на непрерывность в этих точках.

а). х₁=0. ;

Таким образом, в этой точке совпали значение функции с ее левосторонним и правосторонним пределами, т.е. разрыва нет, функция непрерывна в точке х₁=0.

б). х₂=1. ;

Предел слева не совпадает со значением функции в точке и ее правым пределом, значит в точке х₂=1 имеется разрыв непрерывности 1-го рода, потому что оба предела конечные.

Ответ: разрыв 1-го рода в точке х=1.

Задача 144. Найти производные данных функций:

а) ;б) ;в) ; г) ; д) .

Решение.

а). Применяем правило нахождения производной частного , правило нахождения производной сложной функции: если y=f(u), u=u(x), т.е. y=[u(x)], где функции f(u) и u(x) имеют производные, то и формулы табличного дифференцирования.

б). Применяем правила нахождения производной разности (u±v)´=u´±v´, производной произведения (uv)'= u'v+uv' и табличное дифференцирование.

в). Применяем правило нахождения производной произведения (uv)'= u'v+uv' и табличное дифференцирование.

г). Логарифмической производной функции y=f(x) называется производная от логарифма этой функции, т. е. .

Применение предварительного логарифмирования функции в данном случае упрощает нахождение ее производной. Логарифмируем обе части равенства :

, получили равенство, которое и будем дифференцировать.

д). Для вычисления производная функции неявно заданной: переносим всё в левую часть и дифференцируем, после чего выражаем из полученного уравнения у´.

Есть другой способ нахождения производной неявной функции. Пусть непрерывная функция у от х задается неявно уравнением F(x, y)=0, Тогда производную функции у от х можно искать по формуле , если .

Ответ: а). ; б). ; в). ; г). ; д). .

Задача 154. Найти и для заданных функций:

а) б) .

Решение.

а). Применяем правила нахождения производной произведения (uv)'= u'v+uv'.

.

Для нахождения второй производной применяем правила нахождения производной суммы (u±v)´=u´±v´ и частного :

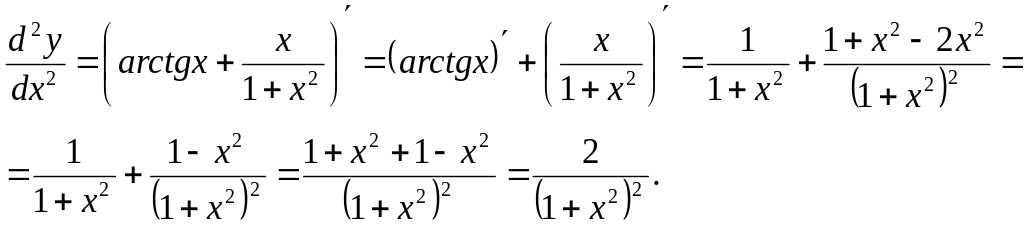
б). Производная параметрически заданной функции находится по формуле .

Вторая производная параметрически заданной функции находится по формуле:

.

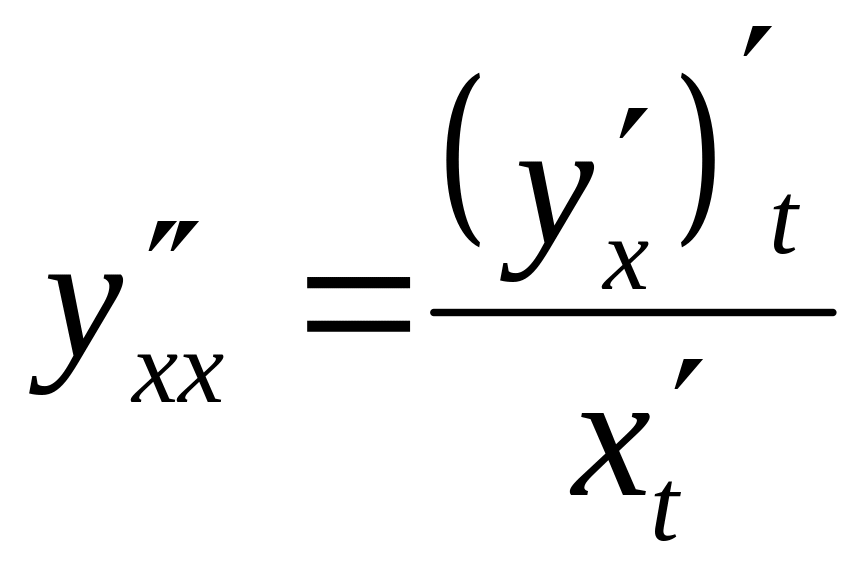Ответ: а). ; б). ;

Задача 174. Найти наибольшее и наименьшее значения функции на отрезке [-3; 1].

Решение.

Чтобы найти наибольшее и наименьшее значения непрерывной функции на отрезке нужно:

• найти производную этой функции и приравняв ее нулю, найти критические точки функции;

• вычислить значения функции на концах заданного интервала и в критических точках, которые в данный интервал попадают;

• среди полученных значений выбрать наибольшее и наименьшее, они и будут наибольшим и наименьшим значениями функции на данном отрезке.

Ответ: наименьшее значение f(1)=-11, наибольшее значение f(-3)=677.

Задача 194. Исследовать математическими методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.