Задача 4
Дана модель Кейнса (одна из версий)
где С – расходы на потребление в период t; Y –совокупный доход в период t; I –инвестиции в период t; T –налоги; К-запас капитала; t – текущий период; t-1 – предыдущий период.
Требуется:
Применив необходимое и достаточное условие идентификации, определить, идентифицируемо ли каждое из уравнений модели.
Определить метод оценки параметров модели.
Записать в общем виде приведённую форму модели.
Решение:
М
одель
включает три эндогенные переменные(Ct,It,Yt)
и две предопределённые(одну экзогенную
переменную - Tt
и одну лаговую-Kt-1).
Проверим необходимое условие идентификации для каждого из уравнений модели.
Первое уравнение:
.
Оно содержит две эндогенные переменные
и 1 предопределенную переменную.
Таким образом, Н=3-2=1, D=2-1=1, т.е. выполняется условие D+1>H.Уравнение сверхидентифицируемо.
Второе уравнение:
.Оно
включает две эндогенных переменных и
одну лаговую(Кt-1).
Таким образом, Н=3-2=1, D=2-1=1, т.е. выполняется условие D+1>H. Уравнение сверхидентифицируемо.
Третье уравнение:
Оно
представляет собой тождество, параметры
которого известны. Необходимости в
идентификации нет.
Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.
|
Ct, |
It |
Yt |
Kt-1 |
Tt |
I уравнение |
-1 |
0 |
b12 |
0 |
b13 |
II уравнение |
0 |
-1 |
b21 |
b24 |
0 |
Тождество |
1 |
1 |
-1 |
0 |
0 |
В соответствии с достаточным условием идентификации ранг матрицы
коэффициентов при переменных, не входящих в исследуемое уравнение,
должен быть равен числу эндогенных переменных модели без одного.
Первое уравнение. Матрица коэффициентов при переменных, не
входящих в уравнение, имеет вид
|
It |
Yt-1 |
|
II уравнение |
-1 |
b24 |
|
Тождество |
1 |
0 |
|
Ранг данной матрицы равен двум, так как определитель квадратной
подматрицы не равен нулю:
Достаточное условие идентификации для данного уравнения
выполняется.
Второе уравнение. Матрица коэффициентов при переменных, не
входящих в уравнение, имеет вид
|
Ct, |
It |
I уравнение |
-1 |
b13 |
Тождество |
1 |
1 |
Ранг данной матрицы равен двум, так как определитель квадратной
подматрицы не равен нулю:
Достаточное условие идентификации для данного уравнения
выполняется.
Таким образом, все уравнения модели сверхидентифицируемы.
Приведенная форма модели в общем виде будет выглядеть следующим
образом:
Задача 5
Имеются условные данные об объёмах
потребления электроэнергии(
)
жителями региона за 16 кварталов:
Год |
Квартал |
t |
Количество потреблённой электроэнергии,yt |
1999 |
I |
1 |
5,5 |
II |
2 |
4,6 |
|
III |
3 |
5,0 |
|
IV |
4 |
9,2 |
|
2000 |
I |
5 |
7,1 |
II |
6 |
5,1 |
|
III |
7 |
5,9 |
|
IV |
8 |
10,0 |
|
2001 |
I |
9 |
8,0 |
II |
10 |
5,6 |
|
III |
11 |
6,4 |
|
IV |
12 |
10,9 |
|
2002 |
I |
13 |
9,1 |
II |
14 |
6,4 |
|
III |
15 |
7,2 |
|
IV |
16 |
11,0 |
Требуется:
1. Построить автокорреляционную функцию и сделать вывод о наличии сезонных колебаний.
2. Построить аддитивную модель временного ряда.
3. Сделать прогноз на два квартала вперёд.
Решение: Построим поле корреляции:
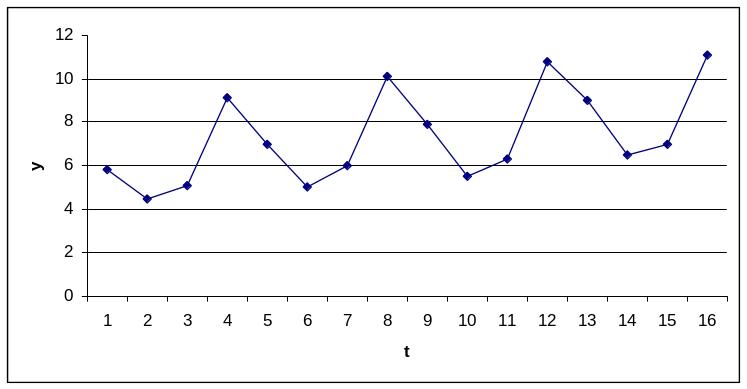
Уже исходя из графика видно, что значения y образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу.
t |
yt |
yt-1 |
|
|
|
|
|
1 |
5,8 |
---------- |
---------- |
----------- |
----------- |
----------- |
------------ |
2 |
4,5 |
5,8 |
-2,7937 |
-1,24 |
3,46425 |
7,805039 |
1,5376 |
3 |
5,1 |
4,5 |
-2,1937 |
-2,54 |
5,572125 |
4,812539 |
6,4516 |
4 |
9,1 |
5,1 |
1,80625 |
-1,94 |
-3,504125 |
3,262539 |
3,7636 |
5 |
7 |
9,1 |
-0,2937 |
2,06 |
-0,605125 |
0,086289 |
4,2436 |
6 |
5 |
7 |
-2,2937 |
-0,04 |
0,09175 |
5,261289 |
0,0016 |
7 |
6 |
5 |
-1,2937 |
-2,04 |
2,63925 |
1,673789 |
4,1616 |
8 |
10,1 |
6 |
2,80625 |
-1,04 |
-2,9185 |
7,875039 |
1,0816 |
9 |
7,9 |
10,1 |
0,60625 |
3,06 |
1,855125 |
0,367539 |
9,3636 |
10 |
5,5 |
7,9 |
-1,7937 |
0,86 |
-1,542625 |
3,217539 |
0,7396 |
11 |
6,3 |
5,5 |
-0,9937 |
-1,54 |
1,530375 |
0,987539 |
2,3716 |
12 |
10,8 |
6,3 |
3,50625 |
-0,74 |
-2,594625 |
12,29379 |
0,5476 |
13 |
9 |
10,8 |
1,70625 |
3,76 |
6,4155 |
2,911289 |
14,1376 |
14 |
6,5 |
9 |
-0,7937 |
1,96 |
-1,55575 |
0,630039 |
3,8416 |
15 |
7 |
6,5 |
-0,2937 |
-0,54 |
0,158625 |
0,086289 |
0,2916 |
16 |
11,1 |
7 |
3,80625 |
-0,04 |
-0,15225 |
14,48754 |
0,0016 |
сумма |
116,7 |
105,6 |
1,49375 |
0 |
8,854 |
65,75809 |
52,536 |
сред.знач |
7,29375 |
7,04 |
|
|
|
|
|
Теперь вычисляем коэффициент автокорреляции первого порядка по формуле :
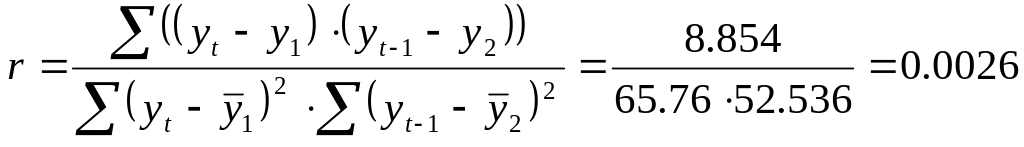
Составляем вспомогательную таблицу для расчета коэффициента автокорреляции второго порядка:
t |
yt |
yt-1 |
|
|
|
|
|
1 |
5,8 |
|
|
|
|
|
|
2 |
4,5 |
|
|
|
|
|
|
3 |
5,1 |
5,8 |
-2,19375 |
-1,24285714 |
2,726517857 |
4,812539 |
1,544694 |
4 |
9,1 |
4,5 |
1,80625 |
-2,54285714 |
-4,593035714 |
3,262539 |
6,466122 |
5 |
7 |
5,1 |
-0,29375 |
-1,94285714 |
0,570714286 |
0,086289 |
3,774694 |
6 |
5 |
9,1 |
-2,29375 |
2,057142857 |
-4,718571429 |
5,261289 |
4,231837 |
7 |
6 |
7 |
6 |
-0,04285714 |
-0,257142857 |
36 |
0,001837 |
8 |
10,1 |
5 |
2,80625 |
-2,04285714 |
-5,732767857 |
7,875039 |
4,173265 |
9 |
7,9 |
6 |
0,60625 |
-1,04285714 |
-0,632232143 |
0,367539 |
1,087551 |
10 |
5,5 |
10,1 |
-1,79375 |
3,057142857 |
-5,48375 |
3,217539 |
9,346122 |
11 |
6,3 |
7,9 |
-0,99375 |
0,857142857 |
-0,851785714 |
0,987539 |
0,734694 |
12 |
10,8 |
5,5 |
3,50625 |
-1,54285714 |
-5,409642857 |
12,29379 |
2,380408 |
13 |
9 |
6,3 |
1,70625 |
-0,74285714 |
-1,2675 |
2,911289 |
0,551837 |
14 |
6,5 |
10,8 |
-0,79375 |
3,757142857 |
-2,982232143 |
0,630039 |
14,11612 |
15 |
7 |
9 |
-0,29375 |
1,957142857 |
-0,574910714 |
0,086289 |
3,830408 |
16 |
11,1 |
6,5 |
3,80625 |
-0,54285714 |
-2,06625 |
14,48754 |
0,294694 |
сумма |
116,7 |
7 |
11,58125 |
1,77636E-15 |
-31,27258929 |
92,27926 |
52,53429 |
сред.знач |
7,29375 |
7,042857 |
|
|
|
|
|
Коэффициент автокорреляции второго порядка равен :
Аналогично находим коэффициенты автокорреляции более высоких порядков, а все полученные значения заносим в сводную таблицу.
Лаг |
Коэффициент автокорреляции уровней |
1 |
0,0026 |
2 |
-0,006 |
3 |
0,002 |
4 |
0,0198 |
5 |
0,003 |
6 |
-0,017 |
7 |
-0,00099 |
8 |
0,029 |
9 |
0.006 |
10 |
-0,07 |
11 |
-0,005 |
|
|
Анализ коррелограммы и графика исходных уровней временного ряда позволяет сделать вывод о наличии в изучаемом временном ряде сезонных колебаний периодичностью в четыре квартала.
Итак, показано, что данный временной ряд содержит сезонные колебания периодичностью 4, т.к. количество потреблённой электроэнергии во второй-третий кварталы ниже, чем в четвёртый-первый. Рассчитаем компоненты мультипликативной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней.
Для этого:
1.1. Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр.3 табл).
1.2. Разделив полученные суммы на 4, найдем скользящие средние(гр.4 табл). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние(гр.5 табл).
№ квартала, t |
Количество потреблённой энергии, yt |
Итого за четыре квартала |
Скользящая средняя за четыре квартала |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
5,8 |
-------------- |
-------------- |
-------------- |
-------------- |
2 |
4,5 |
24,5 |
6,125 |
-------------- |
-------------- |
3 |
5,1 |
25,7 |
6,425 |
6,275 |
-1,175 |
4 |
9,1 |
26,2 |
6,55 |
6,4875 |
2,6125 |
5 |
7 |
27,1 |
6,775 |
6,6625 |
0,3375 |
6 |
5 |
28,1 |
7,025 |
6,9 |
-1,9 |
7 |
6 |
29 |
7,25 |
7,1375 |
-1,1375 |
8 |
10,1 |
29,5 |
7,375 |
7,3125 |
2,7875 |
9 |
7,9 |
29,8 |
7,45 |
7,4125 |
0,4875 |
10 |
5,5 |
30,5 |
7,625 |
7,5375 |
-2,0375 |
11 |
6,3 |
31,6 |
7,9 |
7,7625 |
-1,4625 |
12 |
10,8 |
32,6 |
8,15 |
8,025 |
2,775 |
13 |
9 |
33,3 |
8,325 |
8,2375 |
0,7625 |
14 |
6,5 |
33,6 |
8,4 |
8,3625 |
-1,8625 |
15 |
7 |
-------------- |
-------------- |
-------------- |
-------------- |
16 |
11,1 |
-------------- |
-------------- |
-------------- |
-------------- |
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние(гр.6 табл). Эти оценки используются для расчета сезонной компоненты S. Для этого найдем средние за каждый квартал оценки сезонной компоненты S i . Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.
Показатели |
Год |
|
№ квартала, i |
|
|
|
|
I |
II |
III |
IV |
|
1999 |
|
|
-1,175 |
2,6125 |
|
2000 |
0,3375 |
-1,9 |
-1,1375 |
2,7875 |
|
2001 |
0,4875 |
-2,0375 |
-1,4625 |
2,775 |
|
2002 |
0,7625 |
-1,8625 |
|
|
Всего за i-й квартал |
|
1,5875 |
-5,8 |
-3,775 |
8,1753 |
Средняя оценка сезонной компоненты
для i-го квартала,
|
|
0,53 |
-1,93 |
1,258 |
2,73 |
Cкорректированная сезонная компонента,Si |
|
1,177 |
2,577 |
1,905 |
3,377 |
Для данной модели имеем:
0,53-1,93+1,258+2,73=2.588
Корректирующий коэффициент: k=2.588/4=0.647
Скорректированные значения сезонной компоненты S i получаются при умножении ее средней оценки на корректирующий коэффициент k .
Проверяем условие равенство 4 суммы значений сезонной компоненты:
1,177-2,577+1,905+3,377=4
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины T×E= Y/S, которые содержат только тенденцию и случайную компоненту.
t |
yt |
Si |
yt/Si |
T |
T*S |
E=yt/(T*S) |
Е^2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
5,8 |
0,539 |
10,76067 |
5,7913 |
3,121511 |
1,858075 |
3,452442 |
2 |
4,5 |
-1,939 |
-2,32078 |
5,9989 |
-11,6319 |
-0,38687 |
0,149667 |
3 |
5,1 |
1,267 |
4,025257 |
6,2065 |
7,863636 |
0,648555 |
0,420624 |
4 |
9,1 |
2,739 |
3,32238 |
6,4141 |
17,56822 |
0,517981 |
0,268304 |
5 |
7 |
0,539 |
12,98701 |
6,6217 |
3,569096 |
1,961281 |
3,846622 |
6 |
5 |
-1,939 |
-2,57865 |
6,8293 |
-13,242 |
-0,37759 |
0,142571 |
7 |
6 |
1,267 |
4,735596 |
7,0369 |
8,915752 |
0,672966 |
0,452884 |
8 |
10,1 |
2,739 |
3,687477 |
7,2445 |
19,84269 |
0,509004 |
0,259085 |
9 |
7,9 |
0,539 |
14,65677 |
7,4521 |
4,016682 |
1,966798 |
3,868292 |
10 |
5,5 |
-1,939 |
-2,83651 |
7,6597 |
-14,8522 |
-0,37032 |
0,137134 |
11 |
6,3 |
1,267 |
4,972376 |
7,8673 |
9,967869 |
0,632031 |
0,399463 |
12 |
10,8 |
2,739 |
3,943045 |
8,0749 |
22,11715 |
0,488309 |
0,238446 |
13 |
9 |
0,539 |
16,69759 |
8,2825 |
4,464268 |
2,016008 |
4,064289 |
14 |
6,5 |
-1,939 |
-3,35224 |
8,4901 |
-16,4623 |
-0,39484 |
0,1559 |
15 |
7 |
1,267 |
5,524862 |
8,6977 |
11,01999 |
0,63521 |
0,403491 |
16 |
11,1 |
2,739 |
4,052574 |
8,9053 |
24,39162 |
0,455074 |
0,207093 |
Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T× E . В результате получим уравнение тренда:
T = 0.2076 t + 5.5837
Подставляя в это уравнение значения t =1, 2, ..., 16 , найдем уровни T для каждого момента времени.
Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты. На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.
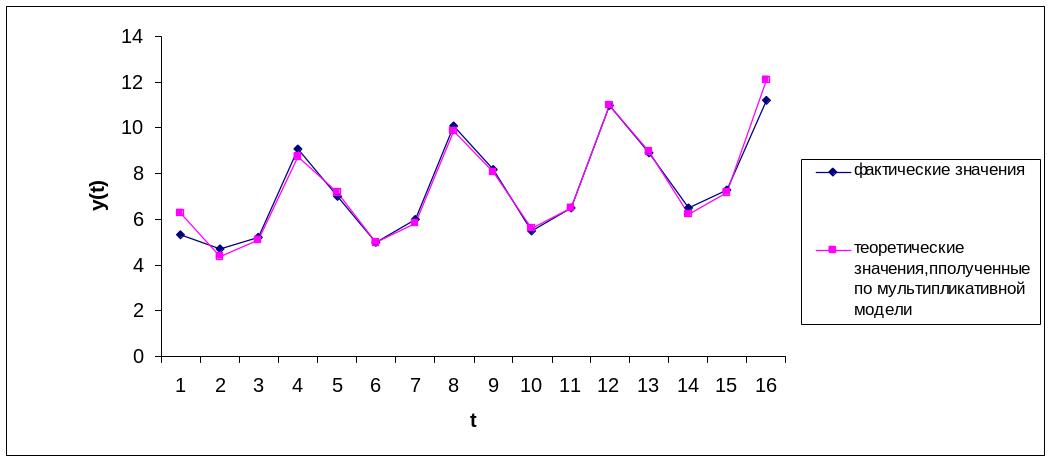
Расчет ошибки в мультипликативной модели производится поформуле: E =Y(T×S) .
Для сравнения мультипликативной модели и других моделей временного ряда можно, по аналогии с аддитивной моделью, использовать сумму квадратов абсолютных ошибок y t /(T×S )2 :
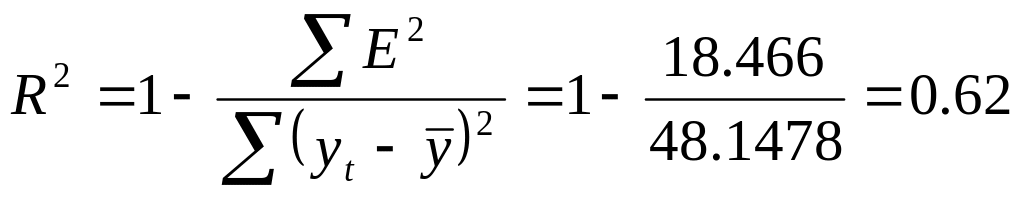
Шаг 6. Прогнозирование по мультипликативной модели. Если предположить, что по нашему примеру необходимо дать прогноз об общем объеме правонарушений на I и II кварталы 2003 года, прогнозное значение F t уровня временного ряда в мультипликативной модели есть произведение трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда T = 0.2076 t + 5.5837
Получим
Значения сезонных компонент за соответствующие кварталы равны:
S1 =1,177 и S2 =2.577 . Таким образом
Т.е. в первые два квартала 2003г. Следовало ожидать порядка 24 и 11 потребления электроэнергии .