3. Определитель третьего порядка. Вычисление определителя с помощью алгеб-раических дополнений (вывод).

Определителем матрицы 3-го порядка это число равное сумме произведений элементов любой строки (столбца) на алгебраические дополнения элементов этой строки ((-1)^ikA_ik).

При вычисление определителя 3-го порядка удобно пользоваться правилом треугольника.

Минором некоторого элемента a_ij определителя k-го порядка называется определитель

n-1 порядка получающегося из одной путем вычеркивания строки и столбца на пересечение которых находятся элементы a_ij . Алгебраическим дополнением a_ij называется минор умноженный на (-1)^i+j A_ij=(-1)^i+j*M_ij .

Знаки миноров:

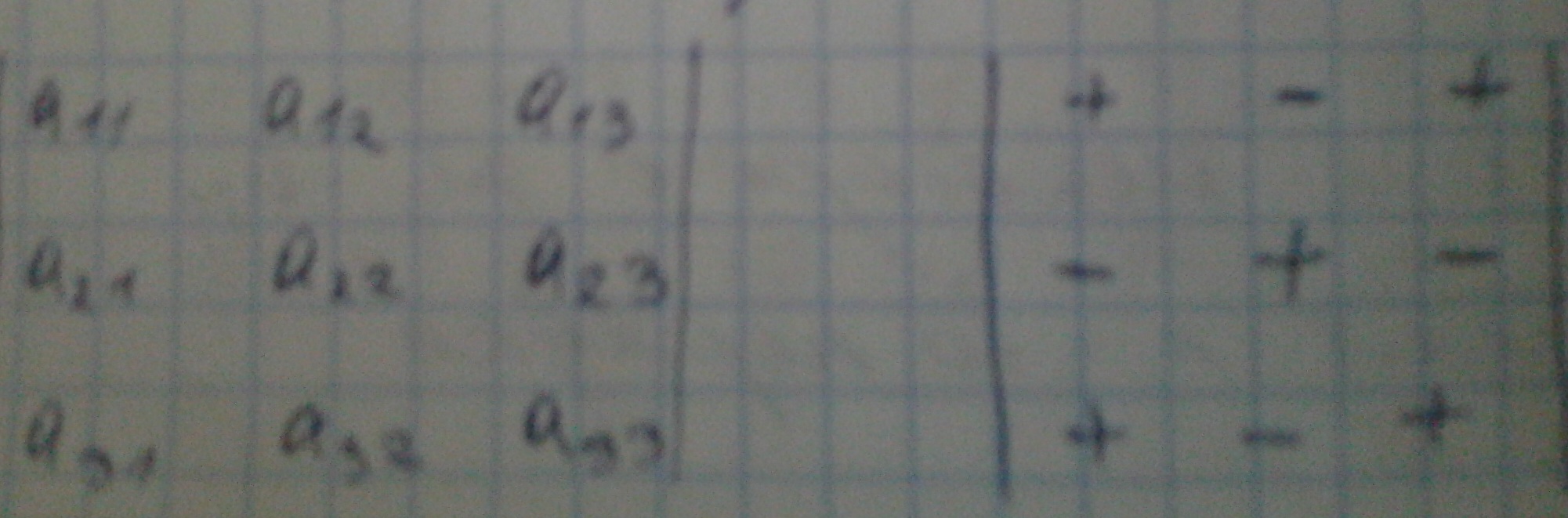
Разложение определителя по элементам строки или столбца: Определитель = сумме произведений элементов некоторой строки (столбца) на соответствующие алгебраические дополнения.

4. Обратная матрица (определение, вывод формулы).

Если определитель квадратной матрицы не равен 0, то такая матрица называется не выраженной, в противном случае выраженной. Матрица обратная квадратной матрице А – это квадратная матрица В удовлетворяющая равенству АВ=ВА. Обратная матрица существует только для квадратной и имеет тот же порядок. Обозначается А^-1.

АА^-1=А^-1А=Е. Алгоритм нахождения обратной матрицы: 1) Найти определитель матрицы А(∆А). Если ∆А = 0, то А^-1 не существует. Если ∆А≠0, то А^-1 существует, то переходим к п.2. 2) Составляем матрицу алгебраических дополнений элементов матрицы А. 3) Записать обратную матрицу А^-1 А^-1 = 1/∆A*Ã

5. Системы линейных уравнений, основные понятия.

Системой линейных уравнений (СЛУ) состоящий из m – уравнений и n – неизвестных называется система вида:

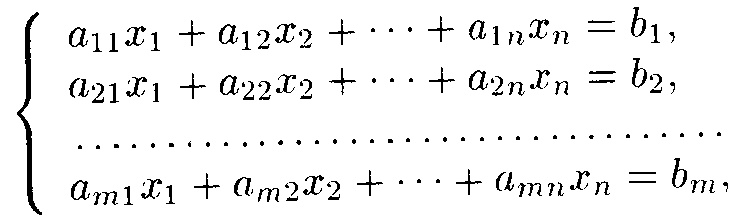(1)

где a_ij (i=1,m , j=1,n) – коэффициенты, b_i – свободные члены, x_j – неизвестное.

Систему (1) можно записывать в матричной форме (А*Х=В) (2), где

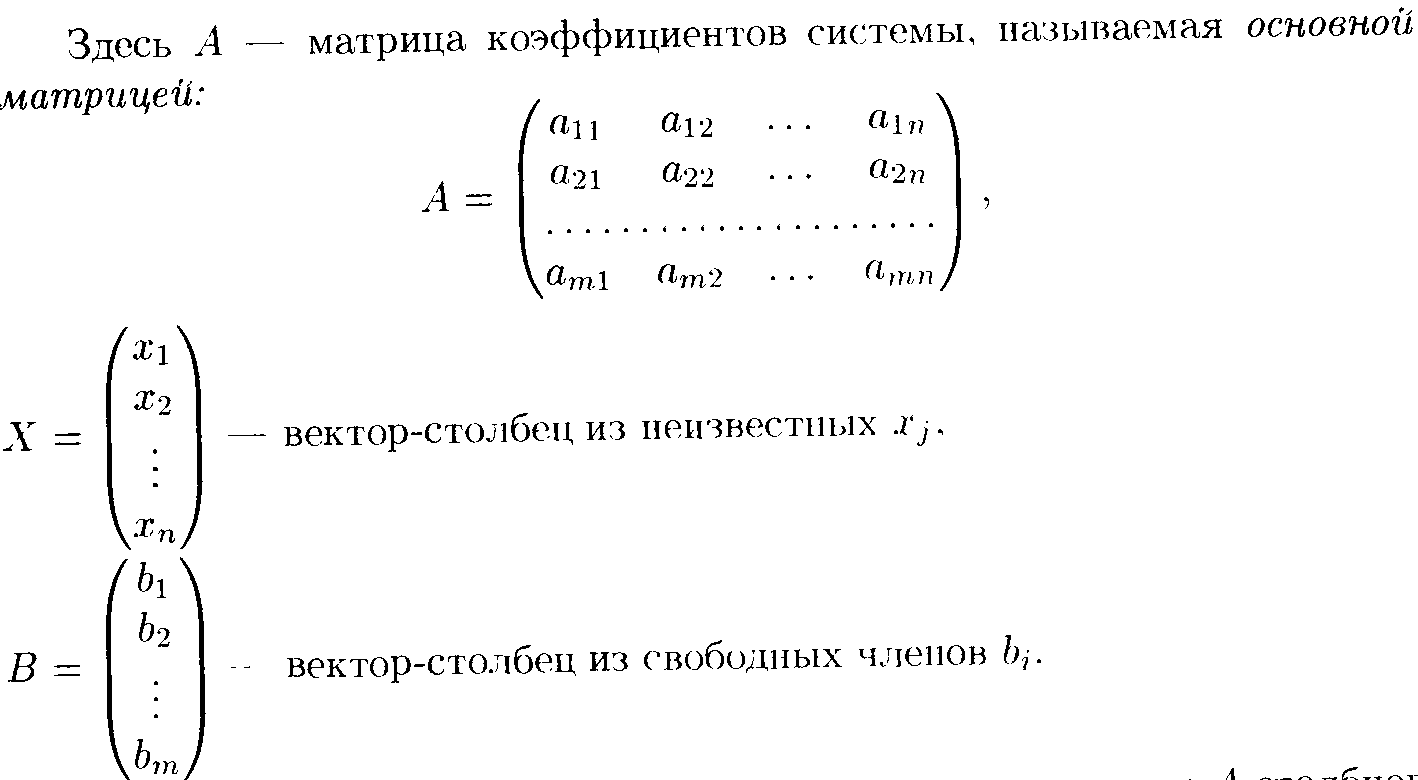
Расширенной матрицей системы (1) называется матрица (Ã(А|В)) дополненная свободным столбцам.

Решить систему значит найти все её неизвестные. Решением системы называют такой набор значений x₁=  ₁, x₂=  ₂, … , x_n=  _n, при котором все уравнения систем (1) обращаются в верные равенства. Решение систем можно так же записать матрицу столбца. СЛУ называется совместной, если она имеет хотя бы 1 решение и не совместной если она не имеет решений.

6. Решение систем линейных уравнений матричным способом.

Матричный способ: А*Х=В (2) домножим обе части равенства (2) на матрицу А^-1 слева.

А^-1 *А*Х= А^-1 *В ≡ Е*Х= А^-1 *В ≡ Х= А^-1 *В (3). Отыскивание решения по формуле (3) называется матричным способом.

7. Решение систем линейных уравнений методом Крамера (вывод).

Для решения СЛУ при m=n можно использовать метод Крамера. Рассмотрим случай m=n=3:

• если ∆≠0, то решение существует и одно ( )

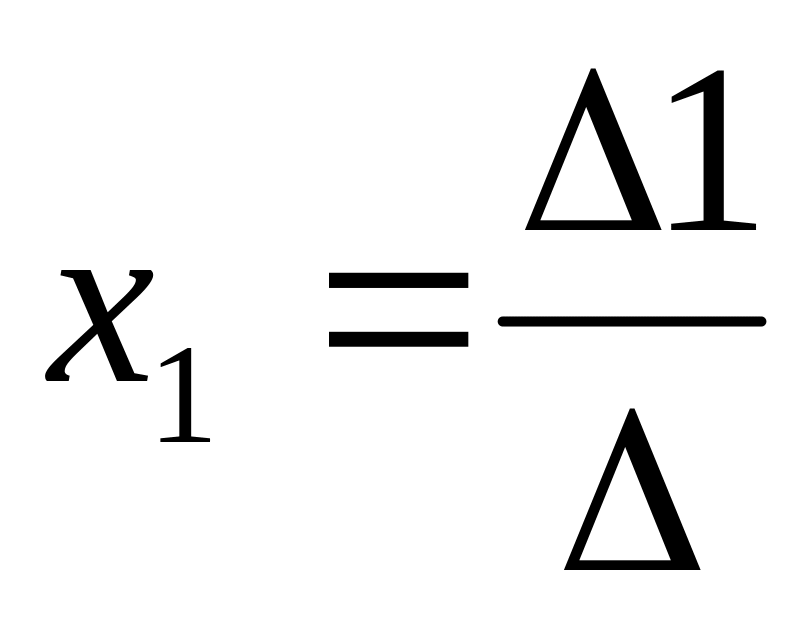• если ∆=0, но ∆₁≠0, ∆₂≠0, ∆₃≠0, то решения нет

• если все ∆=∆₁=∆₂=∆₃=0, то решений бесконечное множество.

8. Ранг матрицы, вычисление ранга матрицы.

Минором k-го порядка произвольной матрицы А называется определитель, составленный из элементов матрицы, расположенных на пересечении каких либо

k-строк k-столбцов. Рангом матрицы А называется наибольший из порядков её миноров отличных от нуля.

Теорема 1:

При элементарных преобразованиях ранг матрицы не изменяется.

Теорема 2:

Ранг ступенчатой матрицы равен количеству её не нулевых строк

Следствие:

Ранг произвольной матрицы равен рангу соответствующей ей ступенчатой матрицы.

9. Решение систем линейных уравнений методом Жордана-Гаусса. Теорема Кронекера-Капелли.

Метод Гаусса – это универсальный способ решения СЛУ с произвольным количеством уравнений и неизвестных.

Достоинство:

1. Менее трудоемкий чем другие методы

2. Позволяет однозначно установить наличие или отсутствие решения, а в случае совместимости найти единственное решение ии бесконечное множество решений.

3. Определяет ранг матрицы системы.

В методе Гаусса применяют прямой и обратный ход. Прямой ход: расширенная матрица системы приводится к ступенчатому виду. Обратный ход: последовательное определения неизвестных из ступенчатой системы соответствующей ступенчатой матрицы.

Теорема Кронекера – Капели: СЛУ (1) совместно имеет решение тогда и только тогда, когда ранг матрицы систем равен рангу расширенной матрицы этой системы.

rang(A) = rang(A|B)

Решение приведением только расширенной матрицы к ступенчатому виду, результаты исследования можно представить в виде схемы:

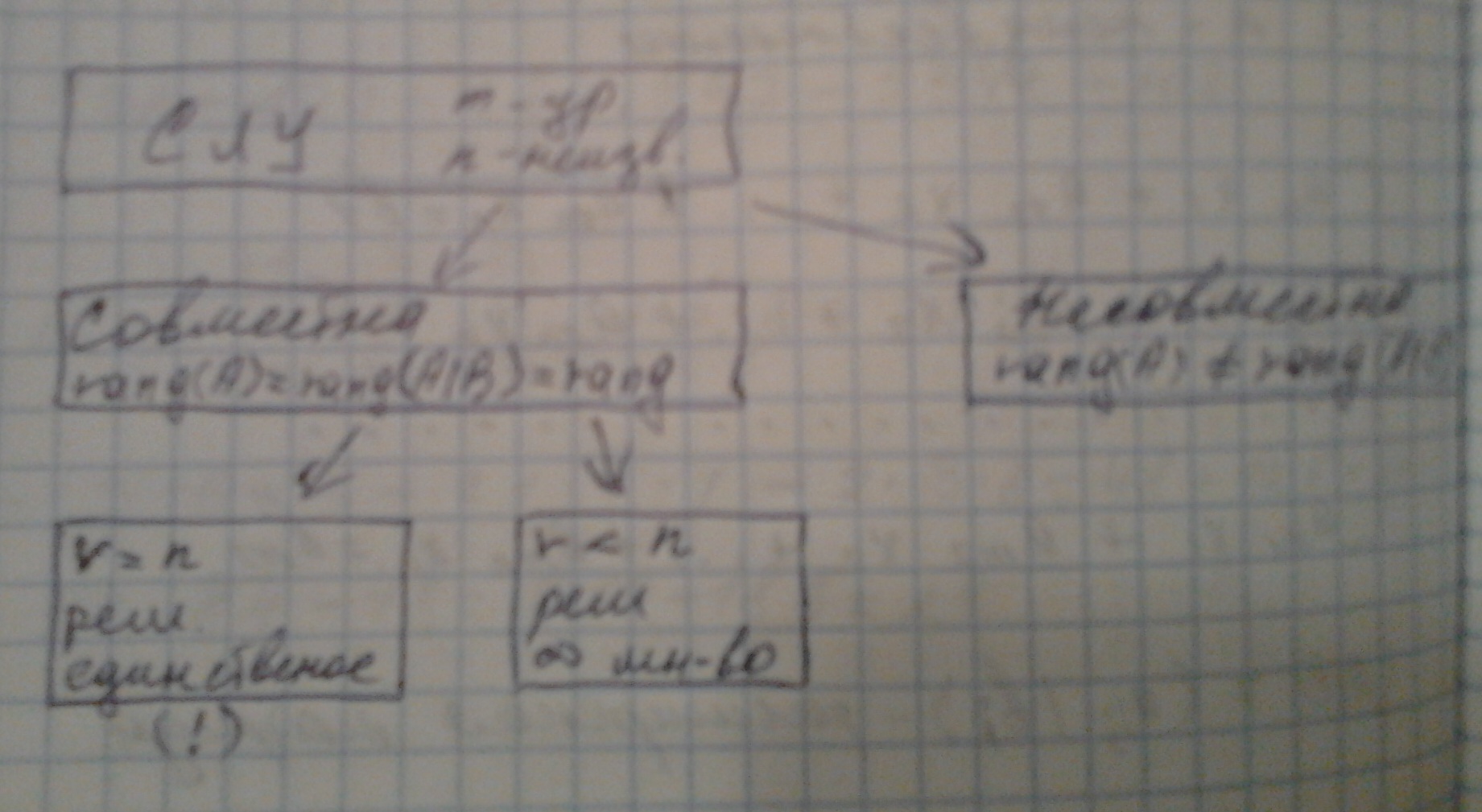
Если r < n т.е. количество ненулевых строк, а значит количество уравнений меньше количества неизвестных. Пусть r переменных: x₁,x₂,…,x_r соответствуют найденному рангу, тогда их называют основными (или базисными) оставшиеся n-r переменных x_r+1,x_r+2,…,x_n называются неосновными или свободными. Свободные переменные могут принимать произвольные значения. Если всем свободным значениям придать значение = 0, то найденное решение называется базисным. Выражая все базисные переменные через свободные можно получить общее решение системы придовая при этом свободным переменным произвольные значения, тогда общее решение будет иметь вид: