13. Прямая как пересечение двух плоскостей определяется совместно заданием двух уравнений первой степени
при
условии, что коэффициенты
,
,
первого из них не пропорциональны
коэффициентам
,
,
второго (в противном случае эти уравнения
будут определять параллельные или
слившиеся плоскости). Пусть некоторая
прямая a определена уравнениями (1),
и
какие угодно числа, одновременно не
равные нулю; тогда уравнение
.
определяет плоскость, проходящую через
прямую а. Уравнением
вида (2) (при соответствующем выборе
чисел
,
можно определить любую плоскость,
проходящую через прямую а. Совокупность
всех плоскостей, проходящих через одну
и ту же прямую, называется пучком
плоскостей. Уравнение вида (2) называется
уравнением пучка плоскостей.
Если
, то полагая
, уравнение (2) можно привести к виду
.
В
таком виде уравнение пучка плоскостей
более употребительно, чем уравнение
(2), однако уравнением (3) можно определить
все плоскости пучка, за исключением
той, которая соответствует
,
то есть за исключением плоскости
.
Например:
Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.
уравнение
этой прямой в отрезках:
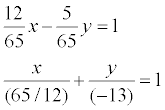
уравнение
этой прямой с угловым коэффициентом:
(делим на 5)
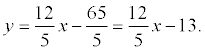
нормальное
уравнение прямой:
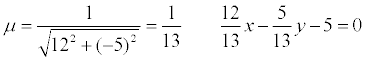
cos φ = 12/13; sin φ= -5/13; p = 5.
14.
Чтобы
найти отклонение какой-нибудь точки
от данной прямой, нужно в левую часть
нормального уравнения этой прямой
вместо текущих координат подставить
координаты точки
. Полученное число будет равно искомому
отклонению.
Чтобы
найти расстояние d от точки до прямой,
достаточно вычислить отклонение и взять
его модуль:
Если
дано общее уравнение прямой
, то, чтобы привести его к нормальному
виду, нужно все члены этого уравнения
умножить на нормирующий множитель
, определяемый формулой
.
.
15. Прямая на плоскости и плоскость в пространстве обладают тем общим свойством, что дополнительная размерность равна единице. Другими словами, что все нормальные векторы к плоскости являются коллинеарными и все нормальные векторы к прямой на плоскости тоже коллинеарны.
Например:
Пусть
заданы две прямые
и
,
. Тогда,
если
, то угол
между
этими прямыми можно найти из формулы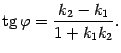
.Если
,то
прямые перпендикулярны.
Как
известно из школьного курса математики,
угловой коэффициент в уравнении прямой
равен тангенсу угла
наклона прямой к оси
. Из рис. 11.10 видно, что
. Так как
,
, то при
выполняется равенство
.
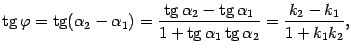Если же
.,то
,откуда
.
Ответ:
16. Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x1; y1; z1) и b = (x2; y2; z2), то сможете найти угол. Точнее, косинус угла по формуле:
Например:
Определить острый угол между прямыми y=−3x+7 и y=2x+1.
Полагая k1=−3k2=2 в формуле tan альфа==k2−k1
1+k1k2
Tan не равен нулю=2−(−3)
1−(−3)умножить2=1, т. е. не равен нулю = пи на4
.