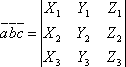9. Векторным произведением вектора a на вектор b называется вектор, обозначаемый символом и определяемый следующими тремя условиями:

- Модуль вектора равен , где - угол между векторами a и b ;

- Вектор перпендикулярен к каждому из вектора a и b;

-Направление вектора соответствует «правилу правой руки». Это означает, что если векторы a ,b и приведены к общему началу, то вектор должен быть направлен так, как направлен средний палец правой руки, больой палец которой направлен по первому сомножителю (то есть по вектору a), а указательный - по второму (то есть по вектору b ).

Векторное произведение зависит от порядка сомножителей, именно:

Само векторное произведение может быть выражено формулой ,где - орт векторного произведения.

Векторное произведение обращается в нуль тогда и только тогда, когда векторы a и b коллинеарны. В частности, .

Если система координатных осей правая и векторы a и b заданы в этой системе своими координатами: то векторное произведение вектора a на вектор b определяется формулой или

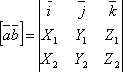
10. Два ненулевых (не равных 0) вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется синоним — « параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

Пусть — векторы пространства . Тогда верны следующие утверждения:

Коллинеарность — отношение эквивалентности, то есть оно:

рефлексивно:

симметрично:

транзитивно:

Нулевой вектор коллинеарен любому вектору:

Скалярное произведение коллинеарных векторов равно произведению длин векторов (взятых со знаком «-», если векторы противоположно направлены)

Векторы на плоскости коллинеарны тогда и только тогда, когда их псевдоскалярное произведение равно 0.

Коллинеарные векторы линейно зависимы.

Существует действительное число такое, что для коллинеарных и , за исключением особого случая . Это определения и также критерий коллинеарности.

На плоскости 2 неколлинеарных вектора образуют базис. Это значит, что любой вектор можно представить в виде: . Тогда будут координатами в данном базисе.

11. Тройкой векторов называются три вектора, если указано, какой из них считается первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись , , означает, что вектор считается первым, - вторым, - третьим

Тройка некомпланарных векторовa a,b ,c называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы a ,b ,c расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.

Смешанным произведенем трех векторов a, b,c , называется число, равное векторному произведению ab , умноженному скалярно на вектор c , то есть .

Если векторы a b,c , компланарны (и только в этом случае), смешанное произведение abc равно нулю; иначе говоря, равенство . Есть необходимое и достаточное условие компланарности векторов a, b, c.

Если векторы a b,c , заданы своими координатами: ; ; ,то смешанное произведение abc определяется формулой: