
- •Определителем второго порядка, составленным из таблицы второго порядка
- •Например:
- •6. Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.
- •Вычисление угла между векторами:
- •9. Векторным произведением вектора a на вектор b называется вектор, обозначаемый символом и определяемый следующими тремя условиями:
- •13. Прямая как пересечение двух плоскостей определяется совместно заданием двух уравнений первой степени
- •Например:
- •Например:
Определителем второго порядка, составленным из таблицы второго порядка
a1 b1
a2 b2
четырех чисел, называется число a1b2 - a2b1.

Определителем третьего порядка, соответствующим таблице (1), называется число, обозначаемое символом
a1 b1 с1
a2 b2 с2
а3 b2 с3
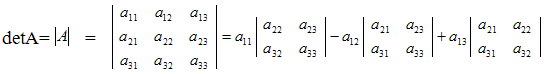
Свойства определителей:
-если одна строка (столбец) нулевая, то оперделитель=0;
-если в определителе строки (столбца) пропорциональные,, то определитель=0
-если к строке (столбцу) прибавить другую строку (столбец), умноженную на любое число, то определитель не изменится;
-если любую строку (столбец) умножить на число К, то определитель увеличится в К раз (общий множитель к строке можно выносить за знак определителя).
2. Вычисление определителя третьего порядка методом разложения по строке или столбцу, используя предварительное преобразование определителя.
Используем следующее свойство определителя :
Если к элементам строки прибавить соответствующие элементы другой строки, умноженные на произвольный множитель, то значение определителя не изменится.
Для столбцов все аналогично.
Найдем det A.
det A = 4 -2 4 =
10 2 12
1 2 2
Из элементов столбца 3 вычитаем соответствующие элементы столбца 1 .
= 4 -2 0 =
10 2 2
1 2 1
Из элементов строки 2 вычитаем соответствующие элементы строки 3 , умноженные на 2.
= 4 -2 0 =
8 -2 0
1 2 1
Разлагаем определитель по элементам третьего столбца.
= ( - 1 )1+3 * 0* 8 -2 +
1 2
( - 1 )2+3 * 0* 4 -2 +
1 2
( - 1 )3+3 * 1* 4 -2 = = 1* 4 -2
8 -2
8 -2
= 1* ( 4 * ( -2) - ( -2) * 8 ) = 1 * 8 = 8
Если в какой-нибудь одной строке или одном столбце присутствует только один элемент, отличный от нуля, то преобразовывать определитель нет необходимости. В противном случае, предварительно преобразуем определитель перед разложением.
3.-Чтобы умножить матрицу на число надо это число умножить каждый элемент матрицы
Например:
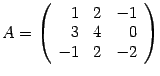 ,
,

Найдите произведения А и B
![]()
![]()
![]()
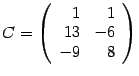
Ответ:
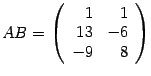
-Складывать (вычитать) можно тотлько матрицы одинаковой формы и размера
А+B=C
Где Cij=Aij+Bij
Например:
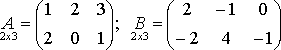
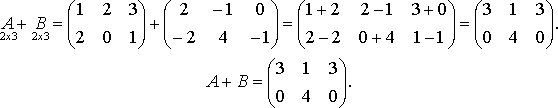
-Делений матриц не существует
4. Правило Крамера:
-Если определитель+0,то
х1=определитель х1 х2=определитель х2 х3=определитель х3
______________; _____________________ ; __________________
Определитель Определитель Определитель
-Если определитель=0, то
1)если определитель х1=определителю х2=определителю х3, то решений бесконечно много.
2)если хотя бы один определитель не равен нулю,то решений нет.
Например:

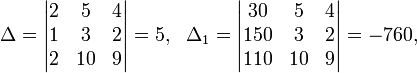
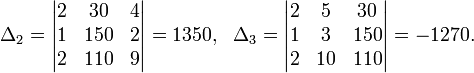
![]()
5. Классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Например:
Пусть исходная система выглядит следующим образом
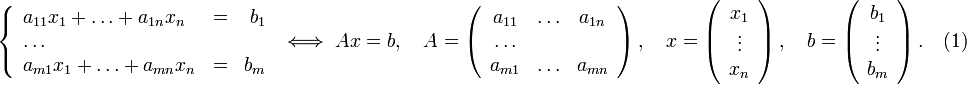
Матрица A называется основной матрицей системы, b — столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):
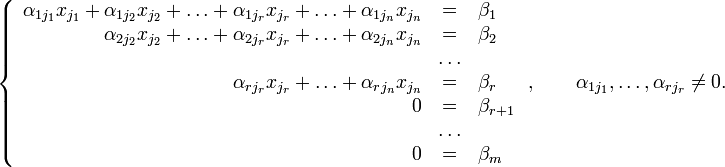
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных [3].
Тогда переменные называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число , где i > r, то рассматриваемая система несовместна.
Пусть для любых i > r.
Перенесём
свободные переменные за знаки равенств
и поделим каждое из уравнений системы
на свой коэффициент при самом левом (,
где — номер строки):
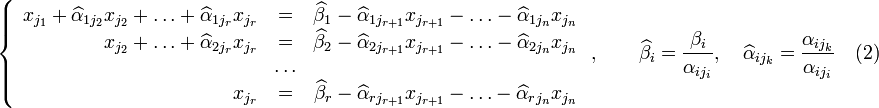
,
где
![]()
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
