Билет №1

1. Вычисление теплоемкостей газов

Теплоемкость-это величина равная кол-ву тепла, которое надо сообщить телу, чтобы изменить его температуру на 1 кельвин.

Теплоемкость C=dQ/T

Удельная теплоемкость c=C/m=dQ/(dT*m)

Молярная теплоемкость CM=C*M

Изохорный процесс V=const

Cv=(i/2)*R

Изобарический процесс P=const

Cp=Cv+R=((i+2)/2)*R

Адиабатический процесс

R/Cv=(Cp-Cv)/Cv

Cp-Cv=Y – показатель адиабаты

pvY=const, где Y>1, pv=const –уравнение Пуассона

Политропический процесс

C=const

N=(C-Cp)/(C-Cv)

N-показатель политропы

pvN=const

Если N=0-изобарический процесс

N=1-изотермический процесс

N=Y-адиабатический процесс

N=+/-∞-изохорический процесс

2. Момент импульса тела. Закон сохранения момента импульса.

Моментом импульса L материальной точки относительно неподвижной точки О называется векторное произведение радиус-вектора r мат. точки, проведенного из точки О на импульс этой мат. точки p=mv

Сумма сил равна произведению массы на укорение

a=dV/dt

Сумма F=ma=m(∆V/∆t)= dt

P=Ft= mV- количество движения

измеряется в (кг*м)/с

F=dP/dt – второй закон ньютона

Скорость изменения импульса равна изменению сумы сил, дейстующих на это тело!

P=Σ(miVi)=mV

F∆t=∆P-импульс силы

Закон сохранения: ΣPi=const

L=[rmv]=[rp]

Билет №2

1. Адиабатический процесс. Уравнение Пуассона.

Адиабатический процесс – процесс, протекающий без теплообмена с окружающей средой, т.е. ∆Q=0.

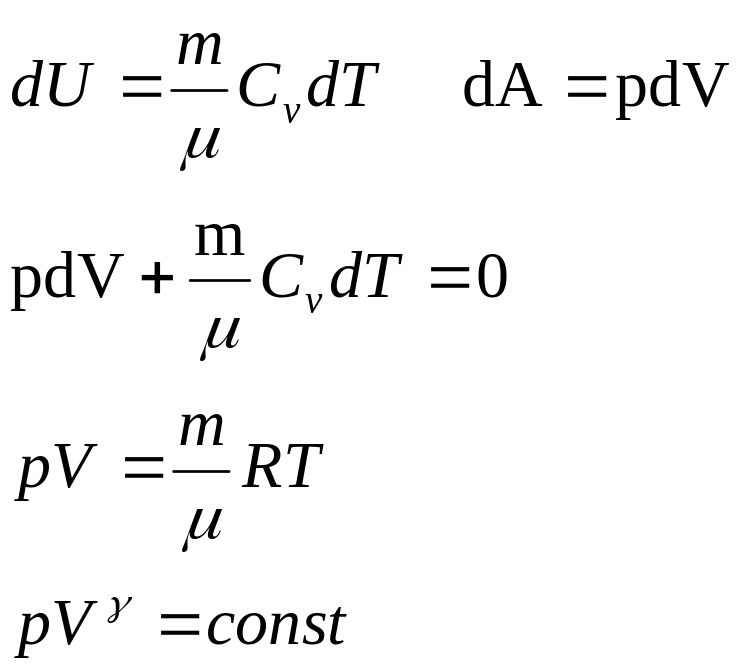
2. Гармонические колебания. Скорость и ускорение при колебательном движении.

Колебательным движением называется периодическим, если значения физических величин, имеющихся в процессе колебания, повторяются через равные промежутки времени.

П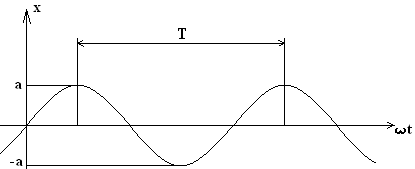 ростейшим видом периодических колебаний являются гармонические – т.е. такие колебания, при которых колеблющаяся величина меняется по закону синуса или косинуса.

А – максимальное отклонение от положения равновесия (амплитуда)

(ωt+α) – фаза колебаний

α – начальная фаза колебаний. Значение фазы в момент времени t=0. Значение начальной фазы определяется выбором начала отсчета времени.

T – период колебаний, промежуток времени, за который фаза колебания получает приращение равное 2π. T=2π/ω. Число колебаний в единицу времени называется частотой. ν=1/T.

Билет №3

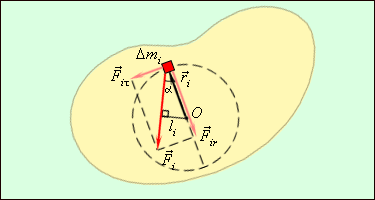
1. Уравнение динамики вращательного движения.

В

торой закон Ньютона может быть обобщен на случай вращения твердого тела относительно неподвижной оси. На рис. 1.23.8 изображено некоторое твердое тело, вращающееся относительно оси, перпендикулярной плоскости рисунка и проходящей через точку O. Выделим произвольный малый элемент массы Δmi. На него действуют внешние и внутренние силы. Равнодействующая всех сил есть е можно разложить на две составляющие: касательную составляющую и радиальную . Радиальная составляющая создает центростремительное ускорение an.

Касательная составляющая вызывает тангенциальное ускорение массы . Второй закон Ньютона, записанный в скалярной форме, дает

где – угловое ускорение всех точек твердого тела. Если обе части написанного выше уравнения умножить на , то мы получим:

Здесь – плечо силы , – момент силы. Теперь нужно аналогичные соотношения записать для всех элементов массы вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M. В итоге:

-основное уравнение вращательного движения